算数の合否を分けた一題（2021年度）

算数の合否を分けた一題

早稲田中入試対策・算数の合否を分けた一題（2021年度）

難易度分類

【１】	(1)A　(2)A　(3)A
【２】	(1)A　(2)B　(3)A
【３】	(1)①A　②A　(2)B　(3)B
【４】	(1)A　(2)B　(3)B
【５】	(1)A　(2)①A　②A

A…早稲田中を目指すなら必ず得点すべき問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難度、処理量から判断して、得点差がつかない問題

問題別寸評

【１】

（1）

数の性質。
見慣れた問題です。1問目という緊張の中で、12でも18でも割り切れる数の個数を出して
解答してしまうことがないよう注意したいです。
確実に正解することが求められます。

（2）

つるかめ算です。1階から29階まで上がるのに何階で階段からエレベータに乗り換えるのかを問われていますが、上がる階数を29階分で計算すると割り切れなくなりあわてた受験生もいたのではないでしょうか。ここで冷静さを失いこの後の問題に影響を受けた受験生もいたのではないかと思われます。1階から29階に上がるには28階分上ればよいことに注意しましょう。

（3）

平均に関する問題。まず、赤玉と青玉の1個当たりの重さを消去算で求めると赤い玉15ｇ，青い玉23ｇとわかります。これら玉の重さの平均が21.2ｇですので、てんびんや面積図を利用し赤い玉と青い玉の個数の比が求められます。

【２】

（1）

角度を求める問題。見慣れた図形の中での角度を求める問題でした。いろいろなアプローチがあると思われますが、いずれにしても容易に正解にたどり着ける問題でした。頂角132°の二等辺三角形に気が付けたかがポイントでした。

（2）

求積の問題です。辺DAの延長した線と辺CBを延長した線の交点を点Gとします。

角DEF＝角ECGだからEFとCGは平行であることがわかります。
三角形DFEと三角形BGAにおいて同位角が等しいので角DFE＝角BAG,角DEF＝角BAG
だから三角形DFEと三角形BGAは相似であり、辺DE＝辺BAであるので合同だということがわかります。したがって、台形FGCEの面積は63㎠で辺EFと辺CGの長さの合計は42cmであることがわかります。EF:CG＝2:5より、EF=12cm。三角形DEFの面積は12×2÷2＝12㎠となり、五角形ABCEFの面積は　63－12＝51㎠となります。

（3）

展開図を組み立て立体の体積を求める問題です。
展開図を組み立てた立体は立方体から全体の6分の1の大きさの三角すいを2つ切り取った立体です。これは早稲田を目指す受験生なら見慣れている立体図形の形です。容易に正解までたどり着けたのではないでしょうか。

【３】場合の数（プレゼント交換）

こちらは「合否を分けた一題」で後述します。

【４】

（1）

直方体の辺上を点が移動する問題。
与えられたグラフより、AB上を5秒，BC上を6秒，CD上を5秒で移動することがわかります。三角形ABDの底辺と高さが5：6で面積が60㎠であることからABの長さが10cmであることがわかります。したがって、点Pの速さは10÷5＝２cm/秒となります。
この（1）で点Pの速さを間違えるとこの後の(2)(3)に影響することになるので確実に正解することが必要です。

（2）

動点を含めた図形が二等辺三角形になるときの時間を求める問題
注意したいのが初めて三角形ABDが二等辺三角形になるときの位置です。点Pが辺BCの真ん中の位置に来たときももちろん二等辺三角形になりますが、実はこれは2回目の二等辺三角形です。辺DA＝辺DPになる二等辺三角形が初めて二等辺三角形になることに気が付かないといけない問題でした。三角形ADPが4回目に二等辺三角形になるのは点Pが辺DE上の点Dから12cmの位置にいるときです。点Pは点Dに着いた後、速さが3cm/秒に変わることに注意してください。12cm÷3cm/秒＝4秒。16+４＝20秒後となります。

（3）

直方体の体積を求める問題。
これは（1）で点Pの速さがわかれば容易に解答まで行きつくことができます。
点Pの速さが辺DE上で3cm/秒になることに注意しながら直方体のたて、よこ、高さの長さを求めるとAB＝10cm、BC＝12cm、DE＝24cmになります。直方体の体積は
10×12×24＝2880㎤　となります。

【５】円の移動（求積問題）

(1)

円が正方形の周りを1周する問題。
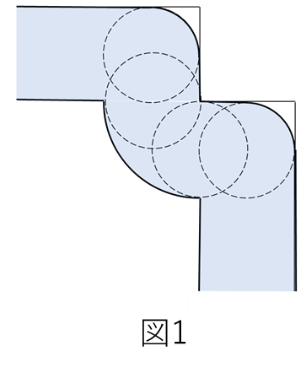
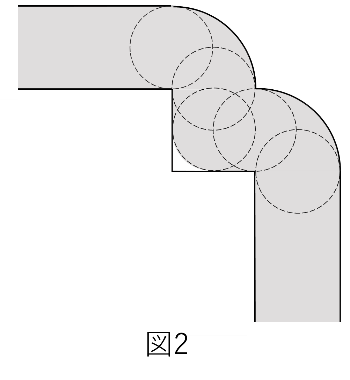
円が正方形の内側にそってを1周したときの円が通ったあとの面積が111.14㎠だから、図1の４つの角の部分を入れると面積は、111.4+0.86＝112㎠になります。ここで、図2の色のついた部分から正方形の4つの角の２×２＝４㎠の正方形を取ると、残りの面積は112−2×2×4＝96㎠となります。長方形1つ分の面積は96÷4＝24㎠、たての長さが2cmだから横の長さが12cmとなります。
よって２+12+２＝16cm　となります。

(2)

図形Xは図1のようになります。

(3)

図形Yは図2のようになります。
図1,図2とも角に注意しながら計算します。
図形Xと図形Yの面積の差を求める問題です。

合否を分けた一題

2021年度の算数は、従来通り大問5つという構成でした。大問2の平面図形に難化が見られたましたが、大問3以降は例年に比べて取り掛かりやすい問題の出題でした。

大問5の円が移動する問題も見慣れた問題ではあるものの、出題の順番が最終問題であったため、慌てて取り組んで計算ミスが生じた受験生もいたのではないでしょうか。ここはしっかり計算ミスせず得点することが必要である問題でした。

大問3は場合の数（プレゼント交換）からの出題でしたが、早稲田中を受験する受験生であればどこかで解いたことがあるはずの問題です。ところが解法手段として多く受験生が樹形図を利用して解いていたのではないかと思われます。今回の出題は樹形図での解法手段は利用できず、誘導に従って順次解答していかなければなりませんでした。そんな状況でも慌てずしっかり誘導にしたがって題意を読み取ることができたかどうかで差がついた問題であるといえます。合否を分けた一題として取り上げます。

【３】

(1)

①3人のうち、1人だけ自分のプレゼントを受け取るときの分け方は、Aさんだけが自分のプレゼントを受け取る場合、BさんがCさんのプレゼントを、CさんがBさんのプレゼントを受け取るときの1通り。Bさんだけが自分のプレゼントを受け取るときもCさんだけが自分のプレゼントを受け取るときもそれぞれ1通りずつだから合計3通り。

②4人とも他の人のプレゼントを受け取る場合を考える問題。

ⅰ）A,B,Cの全員がすでに他の人のプレゼントを受け取っている場合、
Ｄさんは誰と交換してもよいことになります。よって2×3＝6通り。

ⅱ）A,B,Cのうち誰か1人が自分のプレゼントを受け取っている場合
　　ＤさんはA,B,Cのうち自分のプレゼントを受け取っている人と交換すればよいので
　　1×3＝3通り。

ⅰ）とⅱ）をあわせて3＋6＝9通りです。

(2)

4人でプレゼントを交換するとき、1人だけが自分のプレゼントを受け取る場合。
Ａだけが自分のプレゼントを受け取り、他の3人が他の人のプレゼントを受け取るのは2通りだから、Ｂ,Ｃ,Ｄさんがそれぞれ自分だけが自分のプレゼントを受け取る場合もそれぞれ2通りずつあります。したがって2×4＝8通りとなります。

(3)

5人目のEさんを登場させます。すでにⅰ）A～Dさんの全員が他の人のプレゼントを受け取っていた場合とⅱ）A～Dさんのうち1人だけ自分のプレゼントを受け取っていた場合　について考えます。

ⅰ）A～Dの４人とも他の人のプレゼントを受け取る場合は(1)②より9通り。EさんはA～Dさんの誰と交換してもよいので4通り。よって9×4＝36通り。

ⅱ）A～Dのうち誰か1人だけ自分のプレゼントを受け取る場合は(2)より8通り。
EさんはA～Dさんのうち自分のプレゼントを受け取ってしまった1人と交換することになるので8×1＝8通り。

ⅰ）とⅱ）を合わせて36＋8＝44通りです。

著者：坂井智則