算数の合否を分けた一題
早稲田中入試対策・算数の合否を分けた一題(2020年度)
難易度分類
| [1] | (1) A~B (2) A~B (3) B |
|---|---|
| [2] | (1) A (2) A (3) A |
| [3] | (1) A (2) A~B (3) B (4) B |
| [4] | (1) A (2) A (3) B |
| [5] | (1) A (2)① B ② B (3) B |
A…早稲田中合格を目指すなら、確実に得点したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難度、処理量から判断して、得点差がつかない問題
2020年度 出題総評
[1]で数量分野の小問集合、[2]で図形分野の小問集合、[3]~[5]で大問形式での出題と、形式面では例年通りの出題となりました。
実力差がつきそうな問題がほどよく配置されているものの、今年は正答率の極端に低そうな難問は見当たりません。合格レベルの受験生にとっては、例年より易しく感じられたかと思いますが、受験生間での点差はしっかりとついていそうです。
[1][2]や[3]以降の(1)での取りこぼしは致命傷になりかねず、出来る問題を取り切ることが例年以上に重要な入試となりました。
問題別寸評
(1)分数
分母と分子が大きめの分数を題材にした問題は、ここ数年大問1(1)としてよく出題されていますが、今年の問題はやや題意が捉えにくいと感じた受験生もいたかもしれません。
そんなときには、単純な数にして考えてみることが有効です。

(2)ニュートン算
典型的なニュートン算のようですが、よく見ると流出する水が注ぐ水より少なくなっています。水そうを空にするのではなく、逆に空の水そうをいっぱいにするまでの時間の条件が与えられていることが特徴的な問題です。
とは言え、ニュートン算の根本原理が理解できている受験生にとってはほとんど問題ないでしょう。合格レベルの受験生の多くが正解していると思われます。
通常のニュートン算と同じように、1台のポンプが1時間に注ぐ水の量を①、1時間に水そうから流れ出る水の量を1と置いて考えます。
一番目の条件から、③×10-1×10=水そうの容積
二番目の条件から、⑤× 5-1× 5=水そうの容積
これらの差を考えることによって、⑤=5、すなわち①=1であることが分かります。
よって、水そうの容積は⑳と表され、9台のポンプで注ぐときに1時間で水そう内に増える水は⑨-①=⑧となって、求める時間は⑳÷⑧=2.5時間→2時間30分です。
(3)食塩水のやり取り算
早稲田中受験生ならば何度か練習をしているはずの食塩水のやり取り算です。数値はやや煩雑ですが、合格レベルの受験生にとって、内容的にひねったところはありません。
各ビーカーの食塩水全体の量と食塩の量に注目し、下のような流れ図に問題の様子を表します。
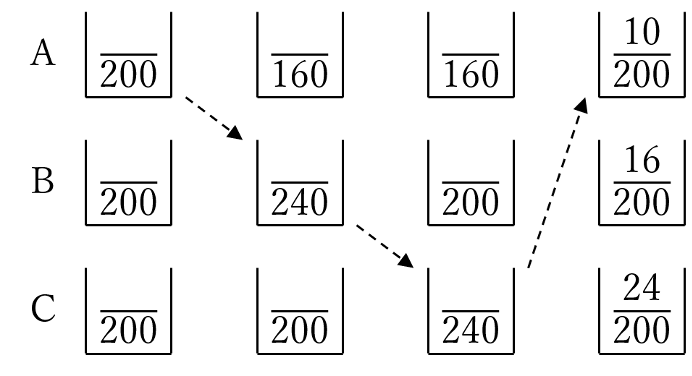
最終結果では濃度が分かっていることから、食塩の量も書き込めます。
ここで最初のやりとりについて考えてみましょう。
Aの容器からは200gの食塩水のうち40gがBに移されたので、Aの中身は160g/200g=4/5が残ったことになります。
また、Cの容器には、このやり取りでは何も変化が起こっていません。
以下、あと2回のやり取りについても、やり取りの前後で容器の中身が何倍になっているかという点に注目してみると、下のように整理することができます。
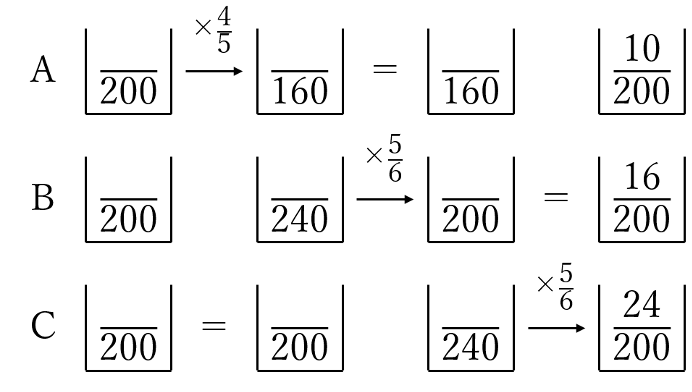
あとは、やり取りの最後から逆算を重ねることで答えを得ることができます。

また、Bに含まれる食塩の量は最後と変わらず16g。そして、やり取りにおいて和が変わらないことに注目すると、Aに含まれる食塩の量は、(10+16+24)-(16+28.8)=5.2gであることが分かります。
以下、同じように最初までさかのぼって計算すれば、答えを求めることができます。
(1)角度(円)
円に絡んだ角度の問題では、中心と円周上の点を結び、二等辺三角形を利用して考えることがポイントになります。

合格のためには落とせない設問です。
(2)正方形の回転移動
回転の様子を自分で描く必要はあるものの、テキストで何度も練習しているタイプの問題です。
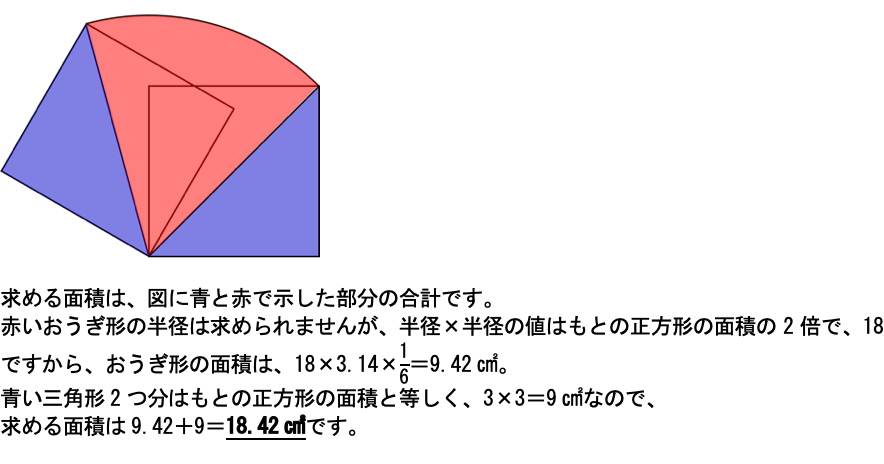
(3)
回転してできるのは、底面の半径6cmで高さ8㎝の円すいから、底面の半径3cmで高さ4㎝の円すいを切り取った円すい台です。
側面積の部分は、もとの円すいの側面から切りとった円すいの側面を引いて求めても充分ですが、相似比と面積比の関係を用いて、切り取った円すいの側面の3倍になっていることを使うとミスが減るでしょう。
こちらも落とせない1問です。
合否を分けた一題として後述します。
(1)
早稲田中受験生なら問題なく処理できるはずですが、比を活用しないと計算がやや面倒になります。
兄が40m進んだところで弟と出会ったということは、弟は100m進んでいます。
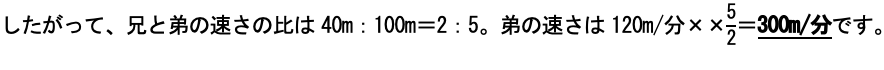
(2)

(3)
ジョギングコースとサイクリングコースの間隔を求めるためには、サイクリングコースの直径が分かれば良さそうです。
そのためには弟の速さを利用してサイクリングコースの1周の長さを求めればよいと気付けば、あとは計算を進めるだけですが、数値はやや煩雑です。ミスには充分注意しなくてはなりません。
(1)と(2)より、弟は分速300mの速さで3時間3分20秒走って、サイクリングコースをちょうど12周しました。

(1)
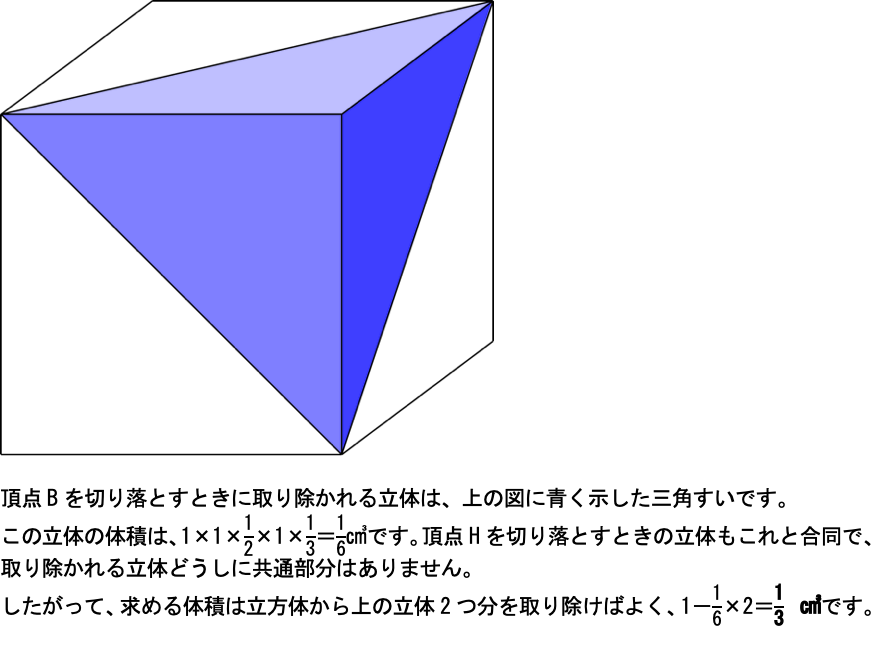
(2)
①
まず、頂点AとBを切り落とした様子を考えます。
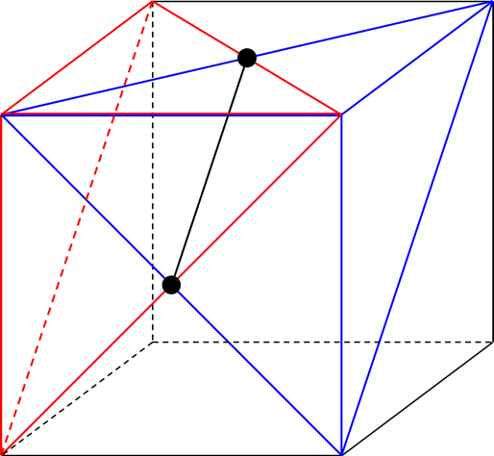
頂点Aを切り落とすときに取り除かれるのは上の図で赤い線で示した三角すい、頂点Bを切り落とすときに取り除かれるのは青い線で示した三角すいです。
立体を取り除いたあとの状態を考えるには、赤い線と青い線の交点(図の黒い点)同士を、黒い太線のように結んでおくことが重要になります。
この太線は、2つの切断面が交わってできる線にあたります。
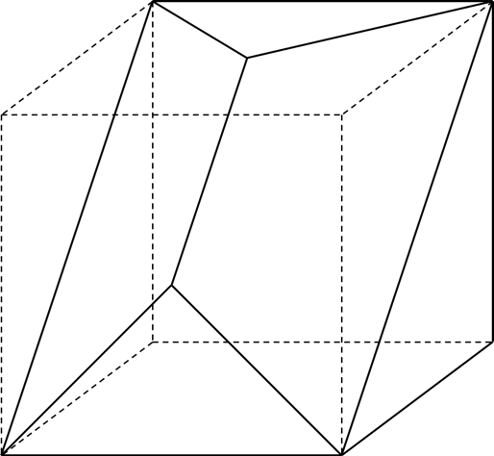
頂点AとBを切り落としたあとは上の図のようになります。さらに頂点GとHを切り落とすと、図の向こう側で同じ立体が取り除かれることになるので…、
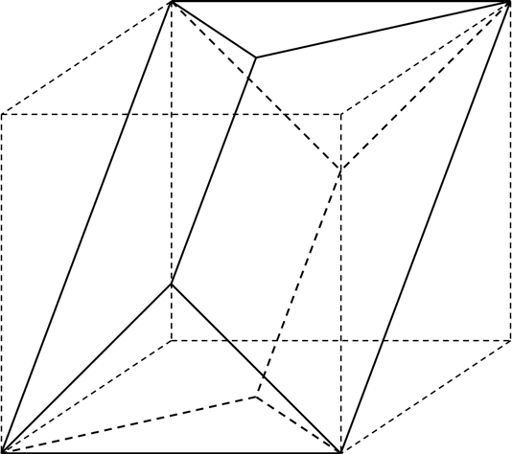
このような立体が残ります。これを右から見た状態を作図すれば答となります。
解答の参考になるように、自分で見取り図を描きながら解き進める必要があり、練習量が充分でない受験生には難しかったかもしれません。
②

(3)
(2)でも見たように、隣り合った頂点を切り落とすと、その切断面同士が交わってできる直線が新しい立体を作ります。

合否を分けた1題
大問3を取り上げます。
(1)(2)あたりまでは、樹形図を描いて数え上げることも不可能ではありませんが、(3)を純粋に書き出しのみで処理するのは困難です。
このような問題では、例えば1秒後の場合の数をもとに2秒後を、2秒後をもとに3秒後を…というように、1つ前の時刻における場合の数をもとに数表にまとめながら解き進めていくことがポイントです。
早稲田中受験生の多くは類題を練習済みだと思われますが、経験の差が処理時間や正答率を分けていそうです。
(1)(2)(3)
まず、点Pが1秒後に各々の頂点にある移動の仕方について考えます。頂点Aにある移動の仕方は0通り、頂点B、C、Dにある移動の仕方は1通りであることは明らかでしょう。
これを、下のような表の形に整理します。
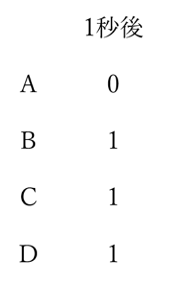
2秒後についても数え上げることは難しくありませんが、後につなげるため、1秒後の数値を用いて次のように考えます。
2秒後に頂点Aにあるということは、1秒後にはB、C、Dのいずれかにいて、そこから移動してきたはずです。したがって、1秒後のB、C、Dの場合の数を加えれば、2秒後に頂点Aにある場合の数が求められます。
いわゆる「道順の問題」(根本原理ポイント365 基礎編096)と似た考え方です。

2秒後に頂点Bにあるのは、1秒後にA、C、Dのいずれかにある場合なので、それらの場合の数を加えます。

同様に、頂点Cについては1秒後のA、B、Dの値を、頂点DについてはA、B、Cの値を用いて求めます。

3秒後以降も同じようにして、自分自身以外の3点につき1秒前の場合の数を足し合わせることで、順に求めていくことができます。
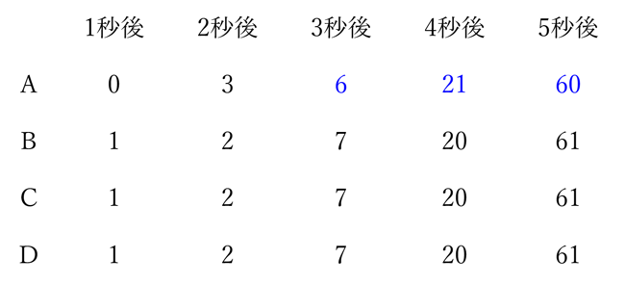
これで5秒後までの表が完成しました。表に青く示した数値が(1)~(3)の答に対応しています。
(4)
与えられた条件を整理すると、
ア 初めの3秒で頂点A→Bと移動する。
イ つぎの3秒で頂点B→Aと移動する。
ウ 最後の3秒で頂点A→Aと移動する。
のようにまとめられます。
アのように移動する場合の数は、上で作成した表から7通り。
イのように移動する場合の数は、図形の対称性を考えるとアと同じで7通り。
ウのように移動する場合の数は、(1)の答そのもので6通り。
よって、求める場合の数は7×7×6=294通りです。
早稲田中入試対策・関連記事一覧
早稲田中入試対策・同じ教科(算数)の記事
- 算数の出題傾向分析
- 算数の合格戦略の提案
- 算数の合否を分けた一題(2012年度)
- 時期による算数の学習法の提案(5年生)
- 時期による算数の学習法の提案(6年生)夏休みまで
- 時期による算数の学習法の提案(6年生)秋以降
- 塾ごとの算数の学習法の提案(サピックス生)
- 塾ごとの算数の学習法の提案(日能研生)
- 塾ごとの算数の学習法の提案(四谷大塚生)
- 算数担当講師から早稲田中学入学を目指す受験生へのアドバイス
- 算数の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2013年度)
- 算数の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2021年度)
早稲田中入試対策・同じテーマ(合否を分けた一題)の記事
- 社会の合否を分けた一題(2010年度)
- 算数の合否を分けた一題(2012年度)
- 理科の合否を分けた一題(2013年度)
- 算数の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2016年度)
- 国語の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2016年度)
- 理科の合否を分けた一題(2016年度)
- 国語の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2017年度)
- 社会の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2018年度)
- 国語の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2019年度)
- 理科の合否を分けた一題(2019年度)
- 国語の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2019年度)
- 国語の合否を分けた一題(2020年度)
- 算数の合否を分けた一題(2021年度)
- 理科の合否を分けた一題(2021年度)
- 国語の合否を分けた一題(2021年度)
- 社会の合否を分けた一題(2021年度)