算数の合否を分けた一題（2019年度）

算数の合否を分けた一題

早稲田中入試対策・算数の合否を分けた一題（2019年度）

難易度分類

[１]	(1) Ａ　　(2) Ａ　　(3) Ｂ
[２]	(1) Ａ　　(2) Ｂ　　(3) Ｂ
[３]	(1) Ａ　　(2) Ｂ　　(3) Ｃ
[４]	(1) Ａ　　(2) Ｂ　　(3) Ｂ
[５]	(1) Ｂ　　(2) ① Ａ　　② Ｃ

A…早稲田中学合格を目指すなら、確実に得点したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難易度、処理量から判断して、失点もやむを得ない問題

出題総評

昨年、久しぶりに復活した「論理推理」や、以前は頻繁に出題された「場合の数」が今年は見られませんでした。一方、昨年は出題されなかった「数の性質」の問題が出題されています。
また、気づきを要求される平面図形や速さの問題など、随所に早稲田中らしさが見える問題構成でした。

問題別寸評

１

(1)は算数の解法知識が試される問題、(2)は典型題です。ここは確実に得点しておきたいところです。
(3)は、問題内容の本質は「数の性質」なのでしょうが、答えの範囲が絞られているため、手を動かして試行錯誤した方が早いでしょう。解法選択の判断が明暗を分けたかもしれません。

（１）

127という素数でしか約分できない分数です。確実に得点したいので、難易度分類ではAにしましたが、「共通な約数が見つけにくい場合は、2数の差を求め、その約数（または差そのもの）で割ってみると良い」という知識は覚えておきましょう。

（２）

言い換えれば、「Ａの容積の５分の４倍とＢの容積の４分の３倍が等しい」ということですから、逆比を利用した基本問題です。確実に得点してください。

（３）

太郎君とお父さんが共に18才ずつ年を取る（年令の和が36増える）ことで、年令の和の十の位と一の位の数字が入れ替わるのですから、和の十の位と一の位の数字は４違う……などと、数の性質を利用して数字を探していくこともできます。しかし、太郎君の年令が12才～15才と絞られていますので、試行錯誤で条件に当てはまる数を探した方が早いでしょう。
「２倍を上回る」は、ちょうど２倍ではだめだということに注意してください。

２

(1)は「相似と線分比」に関するごく基本的な問題です。確実に得点しましょう。
一方、(2)では図形の解法知識（補助線の引き方）を、(3)では知識の活用力を見ようとしているようです。一ひねりあるものの、気づけばごく短時間で解答にたどり着ける問題ですので、点差ができやすい問題だったかもしれません。

（１）

三角形ADGと三角形EBGの相似からBG：GDの比を、三角形ABHと三角形FDHの相似からBH：HDの比を求めて合成し、BG：GH：HDの比を出す基本問題です。

（２）

円の中心同士を結ぶように補助線を引くと、台形全体が、６cm，８cm，10cmの３辺を持つ直角三角形３つに分割できることが分かりますので、台形の下底は12cmです。
エジプト三角形（３辺の比が３：４：５の直角三角形）を知っていれば、より簡単に気づけたかもしれません。

（３）

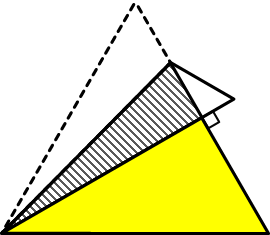
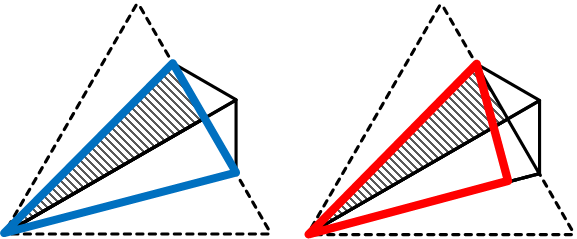
見た目もシンプルで簡単そうに見えますし、気づきさえすれば実際に簡単な問題なのですが、シンプルすぎて糸口が見つけにくかったかもしれません。気づいた人と気づかなかった人とで明暗が分かれたようにも感じます。その意味では、これが「合否を分けた一題」だったかもしれません。
この問題では、折り返した辺が図のように垂直に交わっていますので、図中で黄色くぬった三角形が、元の正三角形の半分、つまり、30度・60度・90度の直角三角形であることが分かります。つまり、斜線部左下の角は15度ということになります。
そこで、右下半分も線対称になるように折り返してみましょう。すると、右図の青線で囲った部分に、30度・75度・75度の二等辺三角形ができます。

これは、等しい辺の長さが分かれば面積をもとめることのできる特殊な二等辺三角形ですから、赤線のような30度・60度・90度の直角三角形（60度の角をはさんだ2辺の比が2：1）を利用することで、青線の二等辺三角形が、底辺6cm，高さ3cmの三角形と分かります。
あとは、それを2等分すれば斜線部の面積を求めることができます。

３

「３量のつるかめ算」を基本とする問題ですが、(1)は単純な差集め算（取り違えの問題と本質は同じ）ですので、難なく解けるでしょう。
(2)，(3)は、不定方程式（いもづる算）に慣れているかどうかで差がついたかもしれません。

（１）

１個100円のシャケ10個（1000円）を除けば、１個あたりの代金が40円違うイクラとタラコが35個で5500円。しかも、数を逆にすると合計金額が200円下がるのですから、イクラとタラコの個数の違いが５個であるとすぐに分かります。
ここで、イクラが１個180円、タラコが１個140円であることを確実に求めてください。

（２）

１個の値段が100円，140円，180円である３種類のおにぎりを、合計45個、6500円で買う方法を、不定方程式（いもづる算）で求めます。
たくさんの個数の組み合わせの中から、もっともタラコの数が多いものを探してください。

（３）

(2)と同様の不定方程式（いもづる算）の答えの中で、シャケの数が多いものから順に、条件に当てはまるかどうかを検証していきます。
一番シャケの数が多いのは、（シャケ19個，タラコ２個，イクラ24個）ですが、タラコ１個を落としてしまうと残りが１個になってしまうので不適です。
二番目にシャケが多いのは、（シャケ18個，タラコ４個，イクラ23個）で、タラコ１個を落とすと３個となり、代わりに加えるのがイクラなら、すべての個数が３等分できる数（３の倍数）になります。

４

速さの問題の常ですが、比を上手に使うことができれば簡単です。見た目の難しさに惑わされず、落ち着いて条件を整理しましょう。

（１）

兄は、1800歩で家まで帰り、200歩だけ引き返したのですから、弟に出会うまでに、学校から家までの道のりの９分の１を戻ったことになります。つまり、出会うまでの間に、兄は道のりの９分の10、弟は９分の８を歩いていますから、速さの比は兄：弟＝５：４となります。

（２）

兄は、家から引き返して弟に出会うまでは５、弟に出会ってからは４の速さの比で歩いています。同じ距離を５：４の速さで歩けば、かかる時間は逆比の４：５となります。
したがって、「弟を迎えに行ってから家に戻るまで」の４分間のうち９分の４が、兄が200歩を歩くのにかかる時間ということになります。その９倍が1800歩、つまり学校から家までにかかる時間となります。

（３）

(2)で、兄と弟が同じ速さ（弟の速さ）で家まで歩いて帰りますが、ここにかかった時間は4分間の９分の５にあたります。また、この距離（兄の歩幅で200歩分）は、学校から家までの道のりの９分の１ですから、弟が学校から家まで歩くのにかかる時間は、4×5/9×9＝20分と分かります。
弟の歩数は１分間に96歩なので、20分間では1920歩となります。学校から家までの同じ道のりを歩くのにかかる歩数の比が、兄：弟＝1800：1920＝15：16 ですから、歩幅の比は 16：15 となり、その差「１」にあたるのが４cmです。

５

立体図形に関する基礎知識を持ち、それを活用できないと解けない問題です。難易度分類では、(1)をBとしましたが、Cに近いBと言えるかもしれません。

（１）

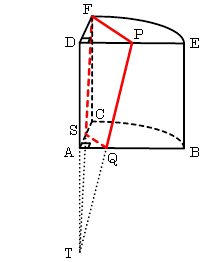
切断面は、右図の赤い線のような台形になります。ここでは、説明のために、切断面が辺ACと交わる点をSとし、DA，PQ，FRの延長線が交わる点をTとしています。
さて、切断した立体のうち、まずは点Ｅを含まない方の体積を求め、それを元の四分円柱の体積から引くことで点Ｅを含む立体の体積を求めていくのが基本方針です。
そして、点Ｅを含まない方の立体は、相似比２の三角すいT-DFPから、相似比１の三角すいT-ASQを切り取った「三角すい台」です。体積比は8：1となりますから、T-ASQの体積を７倍して体積を求めてください。
あとはそれを、四分円柱の体積から引けば完了です。

（２）

➀の展開図は、慎重に考えれば確実に得点できるはずの問題です。図中に与えられたＢ，Ｃの位置関係に気を付けながら想像してみましょう。
一方で、②はなかなか思いつかないかもしれません。展開図までできているので、一見やさしそうに感じますが、いざ解き始めてみると切断面にあたる三角形FPRの面積が分からない……という方が多いのではないでしょうか。そこで、本問を「合否を分けた一題」として後述します。

合否を分けた一題

【問題】大問［５］

（２）②

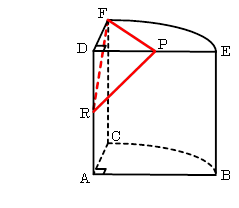
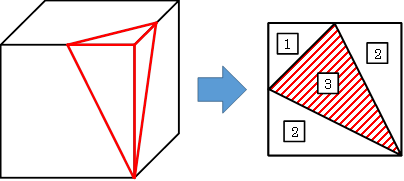
右図は、問題で与えられた立体イに、切り取った三角すいを戻した様子を表しています。この描かれなかった三角すいこそ、この問題の鍵となっていたのです。
この図では長さの感覚がずれてしまいやすいですが、DP＝DR＝2cm，DF＝4cmとなっています。何か連想できたでしょうか？
実は、この三角すいは、下の図の三角すいと同じ形をしているのです。

このように立方体から切り取った三角すいの展開図は正方形になり、面積比が1：2：2：3となることは有名です。展開図となる正方形は、切り取る前の立方体の一つの面と同じ大きさになりますので、本問の場合は1辺4cmということになります。
➀の展開図で書き加えた「さらに切り取る部分」は、底辺6cm、高さ2cmの三角形ですから、この部分も忘れずに引くようにしてください。
（答え）　78.24㎠

著者：澤田重治

この記事は役にたちましたか？