算数の合否を分けた一題（2018年度）

算数の合否を分けた一題

早稲田中入試対策・算数の合否を分けた一題（2018年度）

難易度分類

[１]	(1) Ａ　　(2) Ｂ　　(3) Ａ
[２]	(1) Ａ　　(2) Ａ　　(3) Ｂ
[３]	(1) Ａ　　(2) Ｂ　　(3) Ｃ
[４]	(1) Ａ　　(2) Ｂ　　(3) Ｃ
[５]	(1) Ｂ　　(2) ① Ｃ　　② Ｃ

A…早稲田中学合格を目指すなら、確実に得点したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難易度、処理量から判断して、失点もやむを得ない問題

出題総評

前半は易しく、後半は難しいという問題構成で、取りやすい問題をいかに確実に取れるかが試されるような入試でした。特に大問［１］［２］については、簡単な割に、基本的なことをしっかりと理解していないと解けないという良問でした。
表面的な公式だけでなく、根本原理を押さえる学習が求められています。

問題別寸評

１

(1)・(2)は、いずれも基本的な問題なのですが、見慣れた問題からはひとひねりしてありますので、本質を見抜けたかどうかが問われます。しかし、ここは確実に得点しておきたいところです。
(3)では、３年ぶりとなる推理推論の問題が出されました。

（１）
問題の本質が「ニュートン算」であることを見抜けたでしょうか。珍しい問題設定ですが、早稲田中の合格を勝ち取るためには、確実に得点しておきたい問題です。

（２）
「鉛筆を5本買うと消しゴムが1個ついてくる」というサービスに気を取られてしまうと、なかなか解法の糸口が見えなくなってしまうかもしれません。
サービスでついてくる消しゴムには料金が発生しないのですから、「いもづる算」とか「不定方程式」とかと呼ばれる手法で940円になる買い方を探しておいて、買った鉛筆の本数に応じてもらえる消しゴムの数を足せば良いのです。
最後に、鉛筆の本数と消しゴムの数が「互いに素」となってしまっているものを、忘れずに省いてください。

（３）
試行錯誤の中で発見できる問題なので、正答率はそんなに低くない問題でしょう。ただし、ちょっとしたことに気付けたかどうかで、解答にたどり着くまでにかかった時間が違ってきたはずです。
この問題では、7人中4位がＧさんと決まっています。ここで、ＡさんとＣさんのように、間に2人のランナーをおくためには、間の2人のうちどちらかがＧさんでなければなりません。これは、ＤさんとＢさんも同様です。
一方、最後にＡさんが３人抜かしていますが、途中経過で3位以内にいたら3人抜かすことはできませんので、途中経過のＡさんは、Ｇさんより後ろだったことが分かります。

２

(1)では計算力を、(2)では正確な作図力を、(3)では発想力を見ようとしているイメージです。(2)などは、図だけ見ると複雑そうですが、転がり移動の基本が分かっている人にとっては簡単です。

（１）

半円の方は半径が分からない円の面積ですが、定番問題ですので、おそらく早稲田中を目指してきた人であれば、どの受験生も迷わなかったでしょう。
重なりの部分となる直角二等辺三角形の面積を引くのを忘れないようにしてください。

（２）

曲がる部分については、どの受験生も典型題として扱ってきているはずですから、おそらく悩まなかったでしょう。もし、悩む部分があるとするなら、動き始めた直後のへこみのようなところです。
ここは、ちょっとした溝に自転車の車輪がはまってしまったようなイメージをしてもらうと分かりやすいでしょう。１辺3cmの正三角形が見えたら

（３）

本問を、「合否を分けた一題」として、詳しく後述します。

３

ボールが跳ねる問題も、割合の定番問題と言えるでしょう。
跳ねる回数が多いことと、高さの分からない台があることが問題を複雑にしていますが、地道に計算をしていけばさほど難しくはありません。

（１）

ボールを落とした位置から順番に計算していくだけですから、ここは簡単です。
答えを(2)でも使いますので、ミスなく、きっちり得点してほしい問題です。

（２）

ボールは、「落ちる高さに対して、いつも50％の高さまで跳ね上がる」のですから、ウとエの高さの差は、落ちた高さ（ウの高さ－台の高さ）の50％にあたります。
与えられた図と実際の数字がまったく違います。図の見た目に騙されないように気をつけてください。

（３）

(2)で台の高さが求まっていれば、この(3)は簡単です。(2)を解いた人へのご褒美――「ボーナス問題」というイメージです。
(2)では、数値の大きさの違いに違和感を覚えた図も、(3)ではしっくりくると思います。

４

連結部分を別に計算しなければならないことによって、「植木算」の要素が加わった「通過算」です。
条件を整理し、比を上手に使えたかどうかがカギとなります。

（１）

この問題は、比が利用できれば簡単です。全体的に難しい大問４ですが、早稲田中の合格をつかみ取るためには、ぜひとも正解してほしい問題です。
ポイントとしては、すれ違う場合も追い越す場合も、普通列車の長さと貨物列車の長さの和を距離として計算しているので、かかった時間（14秒と70秒）の逆比が、普通列車と貨物列車の「速さの和」と「速さの差」の差だということです。
最期は「和差算」を用いてそれぞれの速さの比を求めます。

（２）

同じ向きに走っている貨物列車で比較した時、追いついてから追い抜くまでに、16両編成なら70秒、11両編成なら57秒かかります。普通列車が貨物列車を追い抜くので、車両の数にかかわらず速さは一定ですから、かかる時間の比と合計の長さの比が等しくなります。
１つの連結部分の長さを①ｍとすると、普通列車の長さは（20×11＋⑩）ｍ、16両編成の貨物列車の長さは（20×16＋⑮）ｍ、11両編成の貨物列車の長さは（20×11＋⑩）ｍと表せます。
つまり、｛（20×11＋⑩）＋（20×16＋⑮）｝：｛（20×11＋⑩）＋（20×11＋⑩）｝＝70：57となります。

（３）

難易度分類では「Ｃ」としましたが、実はこの問題、解き方自体はそれほど難しいわけではありません。しかし、問題条件で悩んで、解答を断念した受験生も多かっただろうと思います。
その「問題条件」とはつまり、(2)で求めた連結部分の長さを使って良いのかということです。
一般的には、特別な指示がない限り、小問の中に出てきた条件はその小問の中でしか使えません。そうなると、(2)の問題文中に書かれた「普通列車が同じ向きに走っている11両編成の貨物列車に追いついてから追い抜くまで57秒かかりました」という条件は、本来は(2)の中でしか使えず、この条件を基にして求めた連結部分の長さも、(3)では使えなくなってしまうからです。
ここで、「出題者の意図を読む」ことが求められるのですが、実際問題として、連結部分の長さが分からないと(3)は解けません。
また、(2)の文中でも、「57秒かかったとすると」ではなく「57秒かかりました」と表現していますので、ここは(2)で求めた連結部分の長さ（0.8ｍ）を使って計算しても良いでしょう。
そこまで決断してしまえば、その後の計算は簡単で、極めて一般的な通貨算です。手順としては、
　１．連結部分を0.8ｍとして、与えられた条件から、それぞれの列車の速さを求める。
　２．普通列車（長さ228ｍ）が1500ｍの橋を渡るのにかかる時間を求める。
　３．普通列車より62秒多くかかることから、貨物列車の長さを求める。
　４．車両が20ｍ、連結部分が0.8ｍとして、車両の数を求める。
となります。

５

算数の常として「気づけば簡単」という部分はあるのですが、それでもやはり、全体的に難易度の高い出題です。早稲田中合格を目指す受験生であれば、落ち着いた状態でしっかり考えれば解けると思いますが、入試の中でこの問題を解き切るのは大変です。合格するために……ということであれば、(1)が解ければ十分ですし、他の問題ができていれば(1)さえも不要かもしれません。

（１）

三角形ABCと三角形DBEが、直角をはさんだ2辺の比が１：２である、相似な直角三角形であることに注目します。また、三角形EFCや三角形AGDも同様の相似です。
ここで、正方形である四角形DEFGの1辺の長さを②とおくと、AG＝④，GF＝②，FC＝①となりますから、AC＝⑦と分かります。
つまり、三角形ABCと三角形DBEの相似比は７：２、面積比は49：4となります。
あとは、辺（線分）の比から面積比を求めていけば、正解にたどりつけるでしょう。

（２）

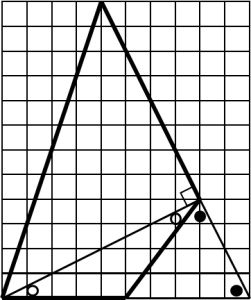
2018_gouhi_sansu
折り返したときに、上の図のような２つの二等辺三角形ができることに気づけたら、正解への道筋が見えてくると思います。
しかし、テスト時間内に手を出すべき問題かどうかの判断を含めて、実際の入試でこの問題を解くのは大変難しいでしょう。
もちろん、解ければ大きなアドバンテージにはなりますが、合否のボーダーライン上において、この問題で合否が決まるということはほとんどないと思いますので、詳細な解説は割愛します。

合否を分けた一題

［２］

（３）

2018_gouhi_sansu_4
四角柱で15cm中12.8cmの深さまで水が入っているので、全体の 2018_gouhi_sansu_2 まで水が入っていることになります。
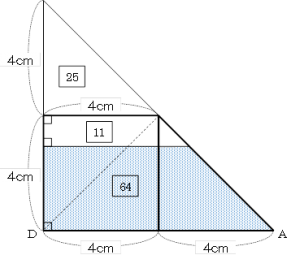
この割合は、面ABCDを下にしても変わりませんから、右図のように辺ADが底辺になる向きから見ると、水の入っている部分の面積が、台形全体のとということになります。
ここで、台形全体の面積を75とすると、水の入っている部分の面積は64、水の入っていない上部の空間は11と表せます。
さらに、この台形は、図のように直角二等辺三角形３個に分けられますので、１つ分の面積は25となります。
この台形の上に、もう一つ直角二等辺三角形をかき加えると、図のように「ピラミッド型」などと呼ばれる相似な三角形ができることが分かります。
白い部分の面積と、かき加えた部分も含めた三角形全体の面積比は、36：100＝9：25です。つまり、相似比は3：5ということです。
したがって、水の深さは8cmの 2018_gouhi_sansu_3 ですので、8× ＝4.8cm　と求められます。
（答え）　4.8cm