算数の合否を分けた一題
早稲田中入試対策・算数の合否を分けた一題(2013年度)
Ⅰ.総括
出題形式は、例年通りの大問5題形式で難易度も極端に難しくなったものなどはない。図形の問題は必ず出題されるので早稲田志望者はどんな図形問題でも解けるように多くの問題に当たっていて欲しい。また、図形の基本事項は必ず頭にいれ、それを自由に使いこなせるようになっておく必要がある。今年度の問題は、問題配置にやや特徴が見られ、5はグラフが出てはいるが、それほど難しくなく、むしろ簡単であり、4に手こずってしまいそこで時間をロスし5にたどり着けなかった生徒が多くいたのではないか。ぱっと全体を見渡して、4を後回しにし5番に行ければかなりの得点を稼げたのではないだろうか。
Ⅱ難易度分析
1. (1)A (2)C (3)B
2. (1)A (2)A (3)B
3. (1)A (2)A (3)B
4. アB イB ウC エC
5. (1)A (2)A (3)A
A:2分以内で解けて欲しい問題。
B:最短の解法ツールを見つけ5分以内で解いて欲しい問題。
C:後回しにした方がよい問題。
1の文章題では、(3)が特に濃度がわからない問題の時の解法を面積図で考えてしまうとドツボにはまってしまうでしょう。結局、BからAへ移した食塩水の濃度がわからない上に、混ぜ終えたAの濃度もわからないので結局面積図で解く比の値を求める方式では解けないことに気付く。そこで式の消去算という結果に繋がるのだが、そこに気付けたかどうかがこの問題を解くポイントになる。
2は、早稲田が必ず毎年出題している図形の問題。正五角形だろうと正三角形だろうと、基本図形に立ち返ることが大切。基本図形とは、結局は、点と辺と角でできているので、この3点の特徴をしっかりと頭に入れておくことである。(1)の正五角形と正三角形は、一辺が共通しているので、必ずどこかに二等辺三角形が出現すると言っても過言ではないでしょう。この二等辺三角形が見つけられたかがポイント。(2)もあらゆるところに相似形が隠れていることに気付けたかどうかなので、結局、相似形とは何かを言えるかどうかということになる。(3)は、やや難しいでしょう。立体の概念が備わっていることが大切。
3は、4年生で学習する植木算と等差数列であるが、ここの計算がしっかり取れていれば問題ないでしょう。ただ、そこが合否の分かれ目だったのではないだろうか。特に(3)。皆がわかるけれども正答にたどり着いたかどうかということがこの問題のポイントでしょう。
4は、速さと比の問題と推理算の混合。図を描いて、どの部分が等しいのか、どの部分で逆比になっているのか、また、進行グラフから太郎と次郎の学校までの時間の比を2通りで表して消去算を使うという方法を取る方がよいでしょう。ただ、そこに気付くまでに相当時間をついやしてしまいがちなので、まずは5番を先にやっておいた方がよかったのではないかと思える問題。
5は、グラフを読み取り、図形の移動の時の重なりの面積や時間を求める問題。かなり簡単であるのでこれは早稲田を志望する生徒は必ず解けていて欲しい問題。しかし、直前の4で時間を費やしていると落ち着いてこの5番が解けなかった生徒もいたのではないだろうか。
Ⅲ.合否を分けた1題
1(3)、または、3(3)が今年の合否を分けた1題ではないか。3(3)は簡単な図を描いて自分が今何グループのどこの長さを出しているのかを把握すればよいでしょう。ただ、1(3)は、解法が色々と考えられるのでここでは、1(3)のわかりやすく時間が短縮できる解法を載せることにする。
1(3)濃度の問題
【解説】
Bの食塩水の濃度を□%とし、移った後のAの濃度を△%とする。
まず、Bから50g, Aに移す時の食塩の量を表す式は、
6%×200g+□%×50g=△%×250g・・・①
次に、△%となったAからBに移した後の食塩の量を表す式は、
△%×50g+□%×50g=9%×100g・・・②
①、②の式より、□%×50gは同じなので、消去算より、
①−②
12g−△%×50g=△%×250g−9g
△%×(250+50)=9+12
△%=21÷300=0.07=7%
よって、混ぜた後のAの濃度は7%なので、そこからは、面積図を使ってもとのBの濃度を求める。
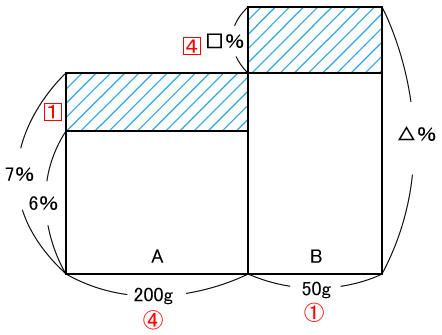
200g:50g=4:1より
縦の比は、逆比となり、1:4=(7−6)%:□%
□=4%
ゆえに、7+4=11 答え11%
早稲田中入試対策・関連記事一覧
早稲田中入試対策・同じ教科(算数)の記事
- 算数の出題傾向分析
- 算数の合格戦略の提案
- 算数の合否を分けた一題(2012年度)
- 時期による算数の学習法の提案(5年生)
- 時期による算数の学習法の提案(6年生)夏休みまで
- 時期による算数の学習法の提案(6年生)秋以降
- 塾ごとの算数の学習法の提案(サピックス生)
- 塾ごとの算数の学習法の提案(日能研生)
- 塾ごとの算数の学習法の提案(四谷大塚生)
- 算数担当講師から早稲田中学入学を目指す受験生へのアドバイス
- 算数の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2020年度)
- 算数の合否を分けた一題(2021年度)