理科の合否を分けた一題（2021年度）

理科の合否を分けた一題

早稲田中入試対策・理科の合否を分けた一題（2021年度）

難易度分類

A…早稲田合格を目指すなら、確実に得点したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難易度、処理量から判断して、部分点を拾えればよしとする問題

１	問１　A　　問２　A　　問３　A　　問４　A　　問５　Ａ問6　Ａ
２	問１　A　　問２　A　　問３　A　　問４　A　　問５　Ａ
３	問１　A　　問２　A　　問３　B　　問４　A　　問５　Ｂ
４	問１　B　　問２　A　　問３　A　　問４　Ａ　　問５　B

出題総評

2021年度の早稲田は、例年通り、基本的知識と論理的な思考力を問う問題が中心でした。
30分40点満点で、本年度の受験者平均27.1点（昨年度26.3点）、合格者平均31.5点（昨年度29.4点）。高かった昨年の平均点を上回っています。
正確さと丁寧さが要求されますが、設定の易しさを考えると、あえて点差が付きにくい設定にしているような印象さえあります。
大問４の（５）も計算問題ですが、この１問でつく差は限定的です。
大問３の化学では難問とまではいかないまでも計算問題が連続していますので、ここでミスせずいけたかどうかで、点差がついたものと考えられます。

2021年早稲田中理科　問題構成

物理分野　振り子の運動
生物分野　光合成
化学分野　金属の燃
地学分野　大地の活動（プレート、地震、海岸段丘）。

問題別寸評

１

（物理）振り子の運動についての問題です。
問４、問６では、振り子の等時性はが振幅が十分小さい範囲で成り立つ、と踏み込んだ内容になっています。小学理科の範囲では、振り子の周期は振幅によらない、とだけ学んでいます。学んできたことを杓子定規に用いると失敗しますが、かなり丁寧な伏線と誘導になっているので、それに沿って動く注意力、読解力があれば正解できるようになっています。

問１

振り子の長さは糸の長さでなく、鉄球の重心までの長さであることを答えますが、選択問題なので、間違えることは難しそうです。

問２

振り子の等時性を発見した人物を選びます。科学史の問題です。

問３

表を見て、振り子の長さが4倍になると、周期が2倍になっていることを読み取ります。受験生の皆さんが何度も練習しているパターンですね。
1周期が6.35÷10＝0.635と分かっているので、長さが16倍になれば周期は4倍になります。

問４

問いから少し離れたところに、
実験A～Cからふれはばのみを大きくしたものが実験D～Fである（※）
と書かれています。
A～Cの結果とD～Fの結果を大きく（＝全体的に）比較すると、D～Fの方が総じて少し値が大きくなっていることが分かりますね。
さらに問４冒頭には
振り子の等時性は、ふれはばが小さい範囲のみで成り立ちます。（※※）
と書かれています。
（※）や（※※）のところを軽く読み飛ばすと、今までの勉強の惰性で
振り子の周期に振れ幅は影響しない
と決めつけてしまい、振り子の長さのみを答えてしまうことになります。

問５（１）（２）

イのようにすると、振り子の長さが変わる（長くなる）ので不適。

問６

問４、問５を踏まえて考えればすんなり答えられそうです。

２

（生物）光合成の基本的な実験についての知識を問う問題です。対照実験については頻出です。

問１

葉緑体を答えさせます。

問２

予想できる結果なので間違えることは困難です。

問３

二酸化炭素を吹き込む前に水の中に溶けている気体を外に出すわけですが、細菌を殺すという選択肢に引っかかった受験生はいたでしょうか。

問４

息には実際色々な気体が入っていますが、BTB液の色を変えるのは二酸化炭素です。

問５

BTB液の色が水草の光合成以外の要因で変化しないことを確かめる「対照実験」に関する問題です。２択にされてしまっているので、間違えにくくなっています。

３

（化学）マグネシウム、アルミニウムの燃焼による質量変化を考えます。

→合否を分けた一題で後述します。

４

（地学）大地の活動（プレート、地震、海岸段丘）ついての問題です。
勉強してきた知識で対応できる問題が中心です。問5は長期の地殻変動を聞く問題ですが、早稲田中頻出のテーマなので、対応できた受験生が多かったのではないでしょうか。

問１

太平洋プレートは分かりやすいですが、フィリピン海プレートも沈み込んでいます。ここでミスする可能性はあります。

問２

地震に関する知識の正確さが問われます。ミスしないように慎重に読むことです。
イ　７段階→10段階
ウ　マグニチュード→震度
です。

問３

液状化を答えさせます。

問４

正断層、逆断層と比べて横ずれ断層がきかれることは稀です。加わる力とずれる向きについて、図を見れば正しく答えられるのでまったく怖くありません。

問５

与えられた条件を用いて、１回の地震で隆起する高さを求めます。
3000年前の侵食面が高さ６ｍになっていることから、
3000年での地面の上昇量が6mであることはすぐにわかるでしょう。
地震は150年周期で繰り返されているので、150年当たりの上昇量を考えると
6÷20＝0.3ｍとなります。
沈降量は１年で6㎜ですから、150年の沈降量は
0.006×150＝0.9ｍとなります。この差が１回の地震による隆起量ですから、
0.9＋0.3＝1.2m＝120㎝と答えが出ます。引き算にしないように注意。
少し長い文章から適切に条件を拾ってくる力が求められます。意味がつかめれば難しくない計算ですが、実際には差がついたと思われます。

合否を分けた１題

全体的に易しいセットでした。それだけに、ミスによる差がでる可能性があるとすれば、大問３の化学計算です。後述するように、邪魔な皿の重さを除いて考えることができたか、混合物の加熱ですぐに算数に持ち込めたか、など練習によって良い動きができた受験生と、その場で考える状態受験生とで、差がついていると考えられます。

３

（化学）マグネシウム、アルミニウムの燃焼による質量変化を考えます。

実験結果には皿の重さ32ｇが含まれています。邪魔なので、32gを取り除いた数値を表に書き込んでいきましょう。表には数値を書き込める程よいスペースがあります。

皿の重さを除くと
加熱前の重さ…マグネシウム・アルミニウムの重さ
加熱後の重さ…生成物の重さ
その差…結びついた酸素の重さ

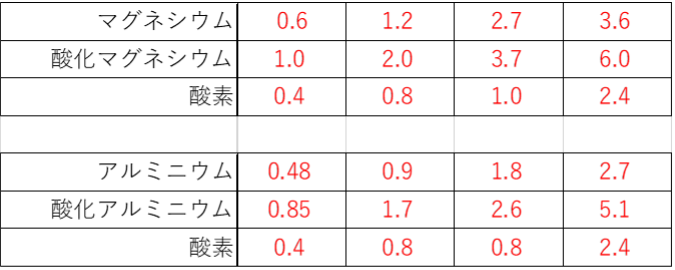
となりますから、ここでは酸素の欄もつけて足して別表を書いてみます。
このようになります。

問１

他の班の実験から、マグネシウムと酸素の重さの比が3:2とわかりますから、３班の2.7ｇに対しては合計1.8ｇの酸素が結びつきます。実験で1.0ｇ増加しているということは、1.0÷1.8＝5/9のマグネシウムが酸化したことがわかります。ですから未反応のマグネシウムは
2.7×4/9＝1.2ｇです。

問２

表を見れば
酸素：マグネシウム＝２：３
酸素：アルミニウム＝８：９
がわかるので、比をそろえておしまいです。

問３

つるかめ算か消去算ですが、自分がマスターしたやり方で答えを出せばよいでしょう。
問2で示された材料を用いて式を立てればよいです。

問４

水素の性質を問う基本的な問題です。

問５

まず問1と同じ要領で、３班の実験２で未反応のアルミニウムの重さを求めます。
完全反応する酸素は1.6g。実験で結びついた酸素は0.8ｇなので、反応した量は1/2です。
したがって、未反応のアルミニウムは
1.8×1/2＝9gです。
あとは、問５で与えられるマグネシウム、アルミニウムとの比を取ることで、水素の発生量は容易に求めることができるでしょう。

著者：大木快

この記事は役にたちましたか？