理科の合否を分けた一題（2019年度）

理科の合否を分けた一題

早稲田中入試対策・理科の合否を分けた一題（2019年度）

難易度分類

A…早稲田合格を目指すなら、確実に得点したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難易度、処理量から判断して、部分点を拾えればよしとする問題

１	問１　B　　問２　A　　問３　A　　問４　A
２	問１　A　　問２　A　　問３　B　　問４　Ａ　　問５　Ａ
３	問１　A　　問２　B　　問３　A　　問４　C　　問５　C
４	問１　A　　問２　A　　問３　A　　問４　Ａ　　問５　Ａ　　問６　B

出題総評

2019年度の早稲田は、例年通り、基本的知識と論理的な思考力を問う問題が中心でした。難易度は、ここ数年、難化と易化を１年ごとに繰り返しており、昨年はやや易しめで、本年は難しめの年でした。

生物分野の問題は、食物連鎖と炭素の循環についての問題。
地学分野の問題は、星の見え方についての問題。
化学分野の問題は、中和熱についての問題。
物理分野の問題は、滑車とてこのつり合いの問題。

生物分野は、昨年に続いて、食物連鎖にからめた問題でした。
化学分野は、中和反応と熱量の計算の両方を、きちんと理解していないと解答できない内容です。
物理分野は、本年も力のつり合いの問題でした。力学分野からの出題は、もはや定番と言ってもよく、普段から難易度の高い問題にも積極的に取り組んで、対策しておくとよいでしょう。
理科は30分40点満点と、時間的に余裕がない中で、いかにすばやく手掛かりを整理し、論理的に考え判断出来るかがポイントとなります。

問題構成は、４分野から大問４題、小問26問。
解答形式は、記号選択が15問、数字が9問、言語が2問。昨年あった作図と記述がありませんでした。
選択肢は、化学のすべてを選ぶ問題について、特に注意が必要でした。
数字は、化学分野と力学分野の両方で出されていて、小問数も倍増しています。計算自体は煩雑ではありませんが、実験の意味と規則性をしっかり把握していることが必要です。
言語は、基本の知識でした。

問題別寸評

１

（生物）食物連鎖と炭素の循環についての問題です。
文章に、「生産者」「一次消費者」「二次消費者」「分解者」の説明がありますが、早稲田中学受験生にとっては、よく知っていることがらです。

問１

「一次消費者」つまり草食動物を選ぶ問題です。クモは肉食、ムカデとモグラは雑食です。ミミズとダンゴムシは、土の中や石の下などにすみ、枯葉なども食べるので、分解者と勘違いしがちですが、一次消費者（草食動物）のなかまです。

問２

空気中の二酸化炭素の割合は、おぼえておくべき数字です。「ppm」についても、説明があるので、それに従って処理します。このとき、ケタを間違えないように注意します。

問３

これも、知識の問題です。増加していることが問題になっているのは、化石燃料の燃焼による二酸化炭素の増加です。また、減少していることが問題になっているのは、砂漠化などによる森林の減少ですから、光合成に関係する矢印を選びます。

問４

食物連鎖の過程で、上位者ほど体内濃度が増加するのですから、分解されにくく、排出されにくい特徴があると考えられます。

２

（地学）星の見え方についての問題です。
冬の大三角は、受験生にとって大変見慣れた天体です。ここは、確実に得点しておきたいところです。

問１

南の空を通る星は、地球の自転によって、東から出て西へ沈むように動きます。

問２

南の空を通る星は、南中高度が高い星ほど、空に出ている時間が長くなります。逆に、南中高度が低い星は、空に出ている時間が短くなります。

問３

南半球では、冬の大三角が北の空に見えます。天球上を、南中している並びのまま移動させます。天頂を通り越して北側にきたところで、観察者が北に向き直って見たときのようすをイメージしてみましょう。

問４

赤色に見えるのは、オリオン座のベテルギウスです。恒星の色は、表面温度に関係があります。これも、基本の知識です。

問５

火星大接近は、大きな話題になっていたので、時事問題として、ほとんどの生徒がチェックしていたはずです。ウ・エ・オは間違いとすぐに判断できるのですが、イで迷ったかもしれません。火星ももちろん満ち欠けをするのですが、水星や金星と比べると、わずかであると考えます。

３

（化学）中和熱についての問題です。
これは、かなり手間のかかる問題です。考え方の指針が４つ示されているので、これを手がかりにします。一つ一つ、積み上げていくように解答していくことが大切です。

問１

塩酸の性質は、基本の知識です。迷うところはなかったはずです。誤ったものを選ぶ問題なので、注意します。

問２

2019_gouhi_rika_01_02

問３

実験１では、水酸化ナトリウム水溶液100cm3と塩酸100/３cm3が中和し、塩酸が余ります。これを加熱すると、塩酸中の塩化水素は気体となるので、塩化ナトリウム（食塩）だけが残ります。

問４

→合否を分けた一題。

問５

４

（物理）滑車とてこのつり合いの問題です。
本年も、早稲田の物理は、力学的分野からの出題でした。定滑車１個と動滑車１個の組み合わせを基本形として、力のつり合いを考えていくなかで、感覚に流されず原理原則に忠実に、ぶれない姿勢で取り組むことが大切です。

問１

糸２にかかる力は、糸１にかかる力の２倍です。この関係は、最後の問題まで変わりません。ここでは、糸２に50gの力がかかるので、糸１には25gの力がかかります。定滑車には、糸１が３か所で下がっているので、ばねはかりには25×３＝75（ｇ）の力がかかります。

問２

太さと材質が一様な棒の重心は棒の中心Oにあり、ここに重さ60ｇがかかっていると考えます。これを、A、Bの２点で支えるのですから、このときの力の配分は、A：B＝２：１とならなければなりません。支える位置は、逆比の関係からAO：OB＝１：２の位置とわかります。

問３

重さも重心の位置もわからない棒のつり合いについて考える問題です。
図３で、Cを支点としたときのつり合いから、（棒の重さが棒を右回りに回そうとするはたらき）＝100×（24÷２）＝1200とわかります。図４のつり合いも同様に、（棒の重さが棒を右回りに回そうとするはたらき）＝（ばねはかりの示す値）×24です。（ばねはかりの示す値）×24＝1200より、ばねはかりの示す値は、1200÷24＝50（ｇ）とわかります。

問４

問５

問３と問４の結果から、Cを150g、Dを50gで支えるとき、棒は水平になることがわかります。力の比が、C；D＝３：１なので、棒の重心は、CE間を１：３に分ける位置です。

問６

合否を分けた一題

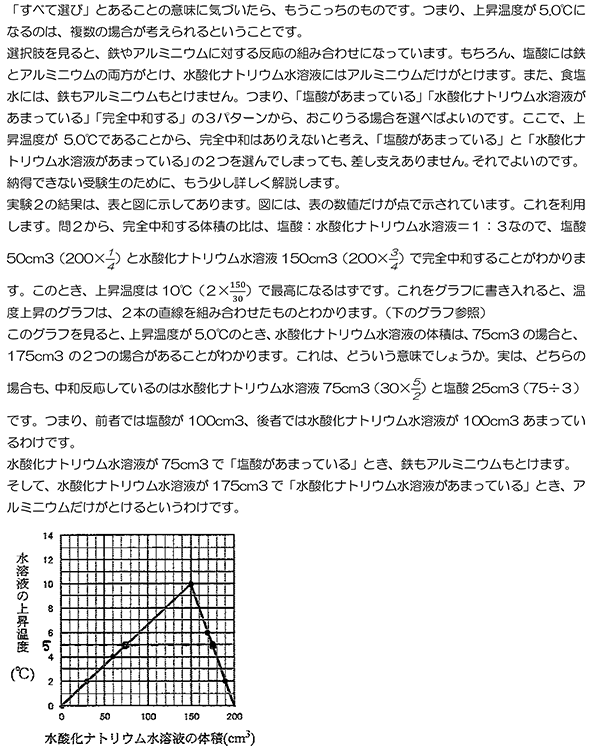
中和反応は発熱反応であることは、早稲田受験生なら知っていることですが、その熱量を計算するとなると、話は別です。実際、化学反応と発熱について学ぶのは高校に入ってからですから、かなり高度な問題といえます。大問３でつまずいてしますと、大問４で時間がなくなり、力が出し切れないパターンが考えられますから、大問３の問４・５を後回しにすることもひとつの手ですが、実は、ちょっと視点を変えると見通しがまったく変わるポイントがあります。そこに気づけたかどうかが合否を分けたと考え、この問題を取り上げました。

３