算数の合否を分けた一題（2018年度）

算数の合否を分けた一題

浦和明の星中入試対策・算数の合否を分けた一題（2018年度）

難易度分類

１	(１)A　(２)A　(３)A　(４)B　(５)B　(６)A　(７)B
２	(１)A　(２)A
３	(１)アB　イB　(２)B
４	(１)A　(２)A
５	(１)A　(２)B　(３)(ア)B　(イ)B

A：明の星合格を目指すなら必ず得点したい問題
B：着眼点や解法ツールにより正答率・かかる時間に差がつく問題
C：難易度や処理量から判断して、部分点狙いで答案を作成すべき、もしくはとばすべき問題

問題別寸評

１

(１)

小数と分数が混ざっていますが、よくある計算問題です。短時間で手早く正解しましょう。

(２)

つるかめ算の問題でしたが、つるかめ算を利用するために必要な値を求められたかという点がポイントでした。最終的にミカンの個数は2人合わせて105個となっています。一度の勝負が決まるごとに2人合わせて7個のミカンを手に入れることになりますので、全部で何回の勝負がついたのかを求めることができます。
105÷7＝15なので、全部で15回勝ち負けの勝負がついたことになります。
あとはつるかめ算を利用して答えを出しましょう。

(３)

浦和明の星女子中学を目指す受験生であれば、普段から何度も何度も目にしたことのある形だったのではないでしょうか。対角線で区切られた下側の八分円から直角三角形と下の四分円の面積を引いて答えを求めましょう。この問題も、手早く確実に正解したい一題です。

(４)

問題を読み、どのような解法に持ち込むかを短時間で決定しなければならない少し面倒な問題でした。３ヶ月分ですので、すべて書き出すこともできますが、工夫をして計算するのと書き出すのとでは５分前後この問題に費やす時間が変わってしまいます。最終的な見直しの時間を確保するためにも、書き出すのではなく周期算を用いて解く練習をしましょう。また、日付けのまま計算するのではなく、4月1日を1日目とした「通し日数」で考えます。例えば、5月2日ならば32日目です。
丸印　　…4の倍数＋1　、三角印　…5の倍数＋1　、水曜日　…7の倍数＋4
この3つの条件を満たす日数を考えると、81日目です。よって、6月20日となります。
普段より、周期算の計算の練習を行っている方にとっては解きやすい問題であったといえます。

(５)

条件整理の問題です。この問題に関しても、浦和明の星女子中学を目指す受験生にとっては手早く確実に正解したい問題です。平均点からクラス全体の合計点を求め、問題１だけ正解した人と問題1・2を両方正解した人の合計点を引いて考えます。
2018_gouhi_sansu1
全体の合計点―(問題1だけ正解した人の合計点＋問題１と２の両方を正解した人の合計点)＝260点―（5点×17人＋15人×10点）＝25点＝問題２だけを正解した人の合計点
問題２は一問5点なので、問題２だけを正解した人は25点÷5点＝5人となります。

(６)

仕事算の問題です。この問題も複雑な問題ではありませんでした。
ウサギは、クラスの半分の人数で60分で折り終えました。カメはウサギより1.5倍の時間がかかり、1日目にはカメの全体の個数の 2018_gouhi_sansu2 を折り終えていますので、１日目と同じ人数であればあと30分ですべて折ることができます。実際は27人が20分で折り終えていますので、(時間の比)30分：20分＝3：2の逆比が人数の比となりますので、27人×＝18人がクラスの半分の人数です。仕事算の人数と時間の比の関係がきちんと理解できている受験生にとっては、解きやすい問題であったといえるでしょう。

(７)

各段ごとに切断の道筋をとらえていきましょう。各段の上の面と下の面の切断線を考えましょう。すると、いくつの立方体が切断されるかが分かります。
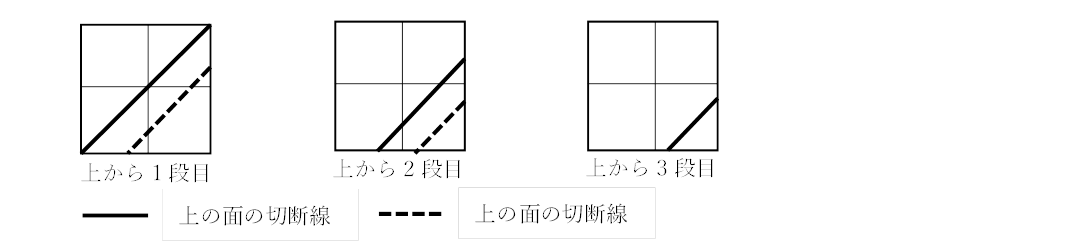
2018_gouhi_sansu3
あとは、切断された立方体を数え上げましょう。短時間でも書きやすい個数・段数の立体切断でしたので、
短時間で丁寧に数え上げることが正解のポイントであった問題でした。

２

(１)

水の体積の比と底面積の比の関係が逆比になっていることをきちんと理解できていれば、手早く正解することができた問題です。明の星女子中学を目指す受験生にとっては必修問題であったといえます。水面の高さが12㎝から16㎝に変わっているので、水そうの底面積と物体を入れた状態での底面積の比は4：3の割合です。比のうちの1にあたる面積が図１の底面積となり、300㎠と求められます。よって、水そうの底面積は1200㎠となります。

(２)

(１)とは異なり、水が入る部分の底面積の大きさが途中で変化する問題です。水の深さが10㎝をこえるときには、10㎝を境に水の入る部分の底面積を変えて計算をしなければなりません。そもそも、この問題は水そうに12㎝の水が入っています。よって、高さ10㎝までと10㎝から上とに分けて計算することさえできれば、難しい問題ではありません。
　　(１)(２)ともに、入試当日までの学習の中で、基本の問題として何度も目にしてきた必須問題の一つといえるでしょう。

３

(１)(２)

ともに、問題文をきちんと読み取り、グラフと連結させて考えることができるかを問われた問題です。グラフを用いて、時間を比に対応させることができていれば、計算もほとんどせずに短時間で答えにたどり着くことができた問題でした。【合否を分けた一題】

４

(１)

食塩水の基本問題です。手早く解きましょう。

(２)

この問題も、浦和明の星女子中学を目指している受験生ならば正解しておきたい問題です。
　　まず、間違ってできてしまった食塩水の濃度(Ａを300ｇ、Ｂを100ｇ混ぜ合わせた食塩水)を求めましょう。すると、6.25％(Ａ′とします)となります。その後、Ａ′の容器から食塩水□ｇを捨て、食塩を□ｇ加え、最終的に濃度と量が予定していた10％で300ｇとなるように求めていきましょう。求める値を間違えないようにだけ注意してください。

５

(１)

そのまま計算しても解くことができる問題でしたが、受験勉強の中で学習した計算の工夫を用いることができれば計算ミスも防ぐことができ、時間を短縮することもできました。いくつかある工夫の中のひとつをご紹介すると、999×999＝(1000－1)×999＝999000－999＝998001という計算方法がシンプルな工夫です。そのまま計算すること、工夫することの２パターンを使いこなせるようにトレーニングし、見直しの際に利用することができたら最適です。

(２)

この問題に関しては、多くの受験生が100桁計算するのではなく、何かしら工夫があるはずだと考えたことと思います。各位の数の和を求める問題ですので、各位の数の和を書き出してみるということを試していれば、すぐに正解までたどり着くことのできる問題です。普段より、分からない問題でもなにかしらの手がかりを見つけ出すために、今できることをするという習慣をつけていた受験生は短時間で正解にたどり着いたはずです。ちなみにこの問題は、9×9＝81⇒和は９、99×99＝9801⇒和は18、999×999＝998001⇒和は27というように計算の答えの各位の和は9の倍数(9×桁数)となっています。よって、100桁のときは900です。
　

(３)

(２)の類題です。同じように、各位の数字が3であるときを求めましょう。(２)の解法に気づくことができれば、(３)についても難なく正解することができた問題です。この大問に関しては、(１)のみの1問だけの正解となるか、全問正解することができるかの、合計点に大きな差がついた一問であったといえます。
(ア)ｂ×ｂ
3×3＝9⇒和は9、33×33＝1089⇒和は18、333×333＝110889⇒和は27
よって、和は9の倍数(9×桁数)です。(ア)は100桁なので、9×100＝900となります。
ｂ×ｂ×２
3×3×2＝18⇒和は9、33×33×2＝2178⇒和は18、333×333×2＝221778⇒和は27
よって、(ア)と同じく各位の数の和は9の倍数(9×桁数)なので、9×100＝900となります。

合否を分けた一題

大問３です。文章問題から読み取ったことをグラフに対応させることができたかどうかがこの問題の鍵となります。まず、どの週がどのグラフにあたるのかを見極めることができているかどうかが第一段階です。
＜１週目＞Ｐ地点から20分間だけ全力で走り、その後はゆっくりと走った。
＜2週目＞Ｐ地点からＱ地点までの道のりの3分の2の地点まで全力で走り、その後はゆっくりと走ったところ、1週目より2分早くＱ地点に着きました。
＜３週目＞Ｑ地点の450ｍ手前まで全力で走ったところ、その後はゆっくりと走ったところ、2週目より5分早くＱ地点に着きました。
＜4週目＞Ｐ地点からＱ地点まで全力で走ったところ、3週目より1分早くＱ地点に着きました。

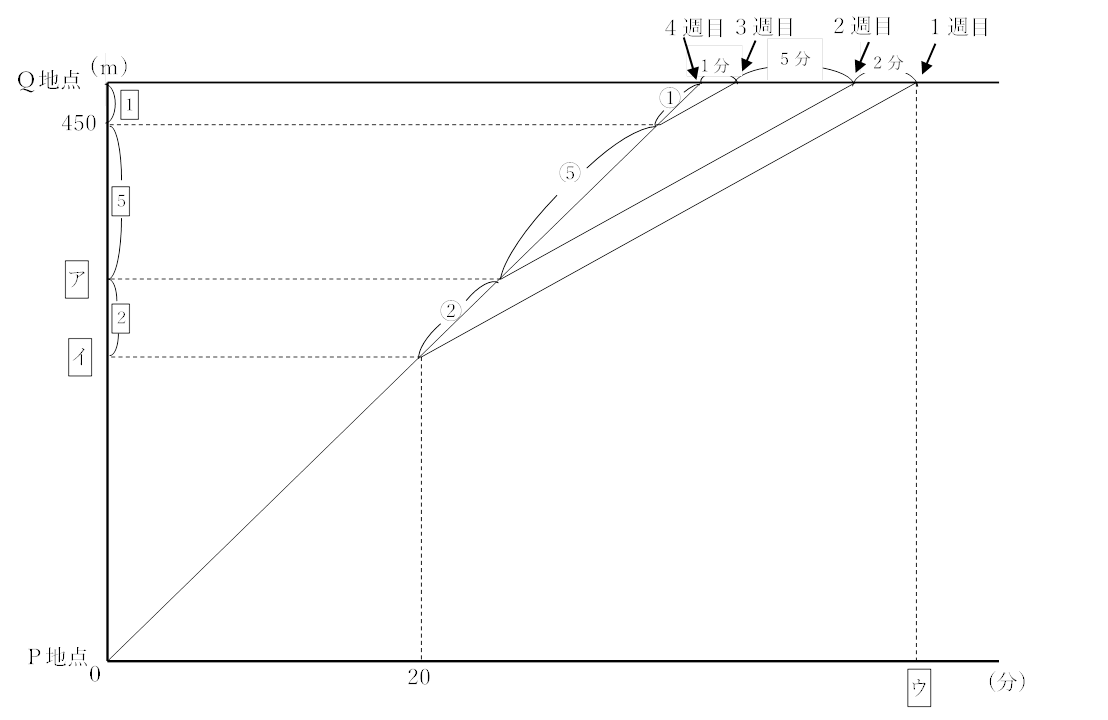
2018_gouhi_sansu4

＜1週目＞～＜4週目＞ともに、ゆっくりと走った部分は速さが等しいので、グラフに書くと平行な線ができます。つまり、20分からウまでのグラフは相似比が1：6：8の相似な図形の三角形となります。よって、上のグラフのように比をおくことができます。
また、２週目はP地点からQ地点までの道のりの全体の3分の２の地点まで全力で走っていますので、残りのアの地点からQ地点まで( 6 )は全体の3分の１となります。ここから、P～Q＝18と求められます。よって、(P地点～イ地点)：(イ～ア地点)：(ア～450ｍ地点)：(450ｍ地点～Q地点)＝10：2：5：1　となり、すなわち、P地点からア地点は450ｍ×12＝5400ｍ、P地点からイ地点までは450ｍ×10＝4500ｍとなります。

(２)(１)より、P地点からQ地点までの距離は450ｍ×18＝8100ｍであり、グラフよりP地点からイ地点までの距離を全力で走ると20分かかることがわかります。つまり全力で走った時の速さは4500ｍ÷20分＝分速225ｍになります。4週目のようにP地点からQ地点まで全力で走ると8100ｍ÷225ｍ/分＝36分　ウの時間は4週目より8分遅いので、36分＋8分＝44分となります。

上の解説のように、速さとしての問題として解くだけでなく、平面図形の問題として解くことにより、容易に答えまでたどり着くことができます。普段より、グラフやダイヤグラムの問題を平面図形としても見ることができている受験生にとっては、解きやすい問題だったといえるでしょう。

2018年の浦和明の星女子中学の第1回入試は全体的にやさしい問題が多かったといえます。算数だけをみれば、高得点勝負であったといえるでしょう。
合否を分けた一題でもあげた大問３や、大問１の(１)～(7)、最終問題の問５のように、時間をかければ数多くの受験生が正解するであろう問題を、いかに短時間で正確に答えを導き出すことができていたかどうかが合格への鍵となりました。日頃から、解法の原理をきちんと理解し、基礎固めをしっかりと行ったうえで短時間で正確に解く訓練を積み上げていくよう心がけて下さい。

著者：受験Dr. (受験ドクター)

この記事は役にたちましたか？