算数の合否を分けた一題
浦和明の星中入試対策・算数の合否を分けた一題（2016年度）
難易度分類
| １ | （１）A （２）A （３）A （４）A （５）B （６）A （７）B |
|---|---|
| ２ | （１）A （２）A （３）A |
| ３ | （１）B （２）B |
| ４ | （１）B （２）C |
| ５ | （１）A （２）C |
A…浦和明の星女子中学合格を目指すなら、確実に得点したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難易度、処理量から判断して、部分点を拾えれば良しとする問題
問題別寸評
（１）
基本的な計算問題です。
0.625＝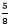
と分数に直して計算しましょう。
（２）
仕事算です。全体量を60と36の最小公倍数の180で置き、それぞれの仕事量を決めてください。
（３）
年令算です。
3年後の3人の年令の和から、花子さんと妹の年令の和を求めれば簡単に解けますね。
（４）
図形の移動の典型問題です。
内側を曲がるときに通過できない部分の面積に要注意。
外側を回転するときは、円の直径2cmが半径の4分円を描きます。
3.14の計算はきちんとまとめて処理して下さい。
（５）
①整数になるものも加えて、7つの分数をグループとして捉えるのがポイントです。
②グループごとに和をとり、等差数列を利用して解くことができます。
（６）
取りちがえ算です。
代金の差を値段の差で割ると、個数の差が求まります。
個数の和と差から、和差算を使って解きましょう。
（７）
ABCで切断した断面図を書き、正三角形を数えるだけです。真ん中のみ白い正三角形となります。
白い部分の面積：黒い部分の面積＝１：３
であることがわかります。
（１）
ダイヤグラムでの速さの出題です。
基本問題ですので、ここでの失点は許されません。
A君は時速５ｋｍで１２分間、B君は時速４ｋｍで9分間移動してQ地点で出会っています。それぞれが移動した距離の和を求めると、１６００ｍと距離が求まります。
（２）
A君が１２分で進んだ距離をB君が何分で進むかを考えましょう。
A君とB君の速さ比は５：４ですから、同じ距離を進んだときの時間比は４：５となります。１２分÷４×５＝１５分
アは２７分となります。
（３）
クロス相似を利用して解くのが良いでしょう。
数値が分数になりますが、冷静に処理して下さい。
（１）
ニュートン算の応用問題です。
ニュートン算をベースにしつつ、条件を少し変化する力と、消去算に持ち込む判断力が問わ
れています。
合否を分けた一題として、後ほど解説いたします。
（１）
条件が多く一見難しそうですが、手を動かして試行錯誤すれば正答にたどり着くのに、そう時間は必要ありません。
最初の状態から順番に追ってゆくと
１、２、３、４、５
↓
５、４、３、２、１
↓
５、２、３、４、１
↓
５、２、３、４、１
↓
５、２、３、２、１
↓
１、２、３、２、１
となります。合計は１＋２＋３＋２＋１＝９
（２）
２の倍数、４の倍数、◎の出る順番を考えましょう。
場合の数の順列により６通り試せばよいことに気付けば、あとは落ち着いて試してゆけばよいですね。
２の倍数⇒４の倍数⇒◎の順で出た場合のみ、条件を満たすことがわかります。
（１）
一本のロープの両側に、同時にロープを繋ぐことができないという条件がポイントになります。まずは（１）で問題の設定をつかみましょう。
①二本ずつペアを作ってゆくと、８本⇒４本⇒２本⇒１本とつながってゆきますから、答えは３分。
②最後に余分な一本を繋げると考え、３＋１＝４分
（２）
時間をさかさまにして、一本の長いロープをどんどんハサミで切ってゆくと考えるとイメージしやすいでしょう。
７分で出来る限り切ってゆくと
１本⇒２本⇒４本⇒８本⇒１６本⇒３２本⇒６４本⇒１２８本
最大は１２８本です。
最小となる場合は（１）の考え方を利用しましょう。
６分でロープを切って作れる最大の本数は６４本。それに１本増やしておけば、７分かかる最小が６５本と求まります。
（２）は難易度が高いので、（１）まで解いて見直しに戻るという判断が適切でしょう。
合否を分けた一題
本年は例年よりも易しい出題が目立ち、高得点勝負になりました。
例年通り典型問題が並んだ１番。２番が易しい速さの出題。
４番、５番は条件にそって手を動かせばよく、処理能力と問題文の読解力を見るための出題でした。算数的な知識に乏しくても、試しているうちに解けたという受験生も多かったのではと推測されます。
その中で合否を分けたのは３番。ニュートン算の応用問題です。
問題文の設定を少し変化させ、既存の解法に持ってゆく力。特にニュートン算から立式して消去算を利用する道筋は、典型題だけを暗記している学習では解き伏せることは難しかったでしょう。
明の星が要求しているのは、解法暗記ではなく、複数の解法パターンを組み合わせて使うレベルであることが感じられる出題です。
以下、解法を示します。
（１）
半分を空にするのに２０日ということから、全て空にするのに４０日であること理解しましょう。同じ量を空にするのにそれぞれ８０日と４０日かかるわけですから、水が減るスピードは逆比の１：２となります。放水量を□、例年の流入量を１００とすると
□－１００＝①
□－８０＝②
という二本の式が立ちます。
①＝２０となりますから、□＝１２０となります。
例年の流入量と放水量の比は１２０：１００＝６：５ですね。
（２）
放水量１２０を７５％にすると９０となります。
９０－８０＝１０ずつもとの量を減らすことができます。
満水時のダムの水量は２０×８０日＝１６００
半分になった時点の水の量は１６００÷２＝８００
８００÷１０＝８０日
ダムの水がなくなるまであと８０日間かかることが求められました。
(3 votes, average: 1.00 out of 5)
Loading ...
浦和明の星中入試対策・関連記事一覧
浦和明の星中入試対策・同じ教科（算数）の記事
他校の同じ教科（算数）の記事
