算数の合否を分けた一題
慶應中等部入試対策・算数の合否を分けた一題(2021年度)
難易度分類
| [1] | (1)A (2)A (3)B (4)B |
|---|---|
| [2] | (1)A (2)A (3)A (4)A (5)A |
| [3] | (1)B (2)A (3)A (4)B (5)B |
| [4] | (1)B (2)B |
| [5] | (1)A (2)B |
| [6] | (1)B (2)C |
A:慶応中等部中合格を目指すなら必ず得点したい問題
B:着眼点や解法ツールにより正答率・かかる時間に差がつく問題
C:難易度や処理量から判断して、飛ばすことも考慮すべき問題
問題別寸評
(1)計算問題
特に工夫が必要というわけでもなく、いたって普通の計算問題でした。
(2)計算問題
逆算の計算問題です。(1)と同様、標準的な難易度の問題です。
(3)曜日に関する問題
基本的な曜日を求める問題ではありましたが、20回目までひとつひとつ出すのではなく、1月138日⇒2月107日⇒・・・のように処理が出来たかどうかはポイントです。
(4)縮尺
これも標準的な問題でした。単位変換はもちろん、分数の形で一気に処理が出来た受験生とそうでない受験生とで、所要時間に差が生まれたと予想できます。
(1)食塩水
やや珍しいタイプの食塩水の問題でしたが、面積図やてんびんを使用すれば手早く処理できる問題でした。
(2)相当算
標準的な相当算です。図を描いて処理するもよし、式で処理するもよし。正確に解ききりたい問題です。
(3)年齢算
標準的な年齢算です。差が変わらないことに注目すれば、正答にたどり着いたはずです。
(4)仕事算
途中で速さの変わる仕事算でした。太郎、次郎、全体の仕事量の比を出し、つるかめ算に持ち込む典型題です。
(5)時計算
標準的な難易度の時計算です。正確に解ききりたい問題でした。
(1)
三角形の相似に関する問題でした。2つの三角形の相似比から辺の長さを出すのではなく、相似な三角形の一番長い辺と一番短い辺の比が3:1であることを利用するとスピーディーに解くことが出来ました。
(2)
おうぎ形の折り返しでは、補助線を引いて正三角形を作ることがポイントです。類似の問題を解いたことのある受験生が多かったと思われます。
(3)
正六角形の面積比に関する問題でした。標準的な問題ですので、分割して手早く処理したい問題です。
(4)
移動範囲の問題に似ていますが、移動する長さを求める問題でした。計算がやや煩雑です。丁寧に処理することがポイントでした。
(5)
回転体の表面積を求める問題です。特別な考え方・解法が必要な問題ではありませんが、角出し、円すいの側面積など基本的な操作を正確に行うことが出来るか試される問題でした。
標準的な速さに関する問題でした。2者間グラフの問題では、状況整理のためにグラフを線分図やダイヤグラムに落とし込むことが肝要です。状況判断さえスムーズに出来れば手早く処理できる問題でした。後ほど合否を分けた一題で解説を致します。
与えられた整数に対して、操作を繰り返す問題です。よく目にするタイプの問題ではありますが、(1)(2)ともに操作数が多いので、正確に作業を行わなければなりません。
(1)
なかなか1にたどり着かず焦った受験生もいたでしょうが、ひとつひとつ丁寧に作業を行いましょう。
(2)
今度は1から遡って考えます。3で割って1余る数は、一つ前の操作において2通りの候補があります。そこだけ注意し、樹形図にまとめることができれば正答にたどり着いたはずです。
図形の分割方法についての問題でした。リード文に場合分けのヒントがありますので、そこに気付くことが出来たかどうか。前の条件を活用し、問題を解いていきます。
(1)
六角形ABCDEFの分割を考えます。
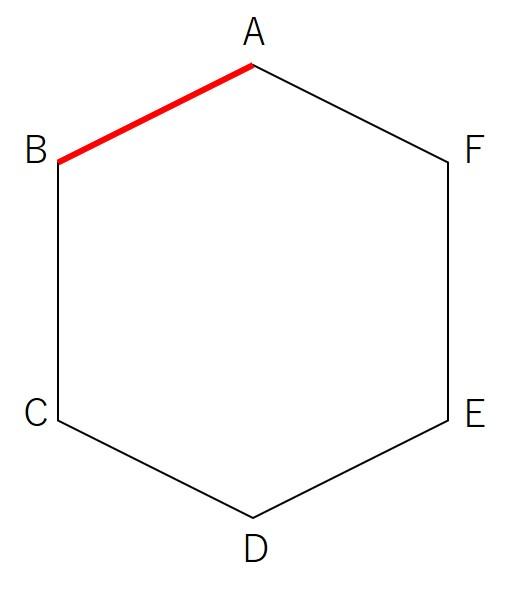
分割にあたり、辺ABを含む三角形をまずは考えます。
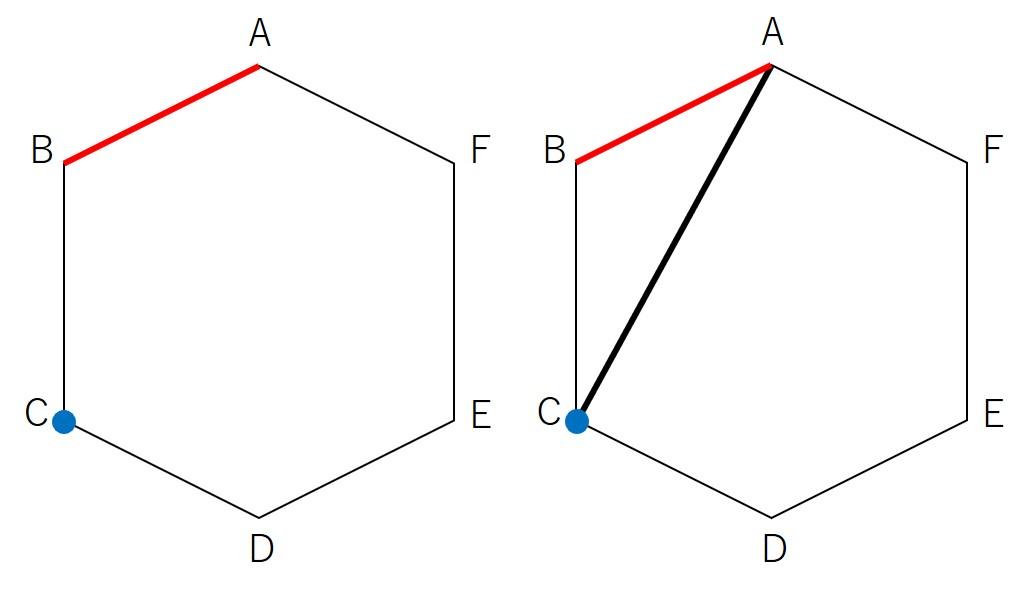
もう1点をCに決めると、三角形ABCと五角形ACDEFに分けることが出来ます。五角形の分割方法はリード文にある通り5通りです。また、対称性より、もう1点をFに決めても5通りの分割方法があることがわかります。
次にもう1点をDに決めます。
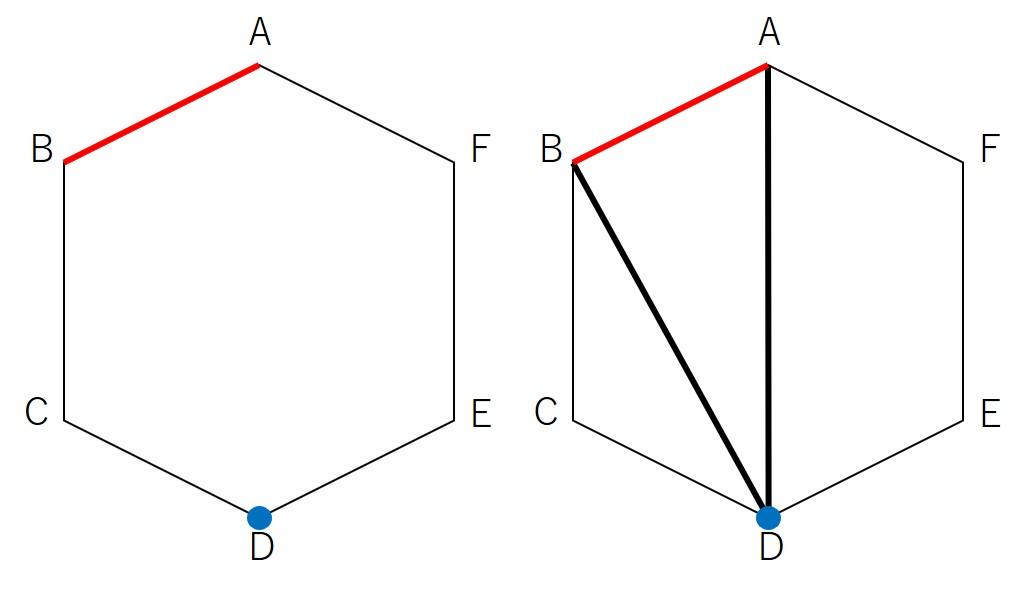
三角形ABD、三角形BCD、四角形ADEFに分割されます。四角形の分割方法はリード文にある通り2通りです。また、これも対称性より、もう1点をEに決めても分割方法は2通りになります。
よって、5+5+2+2=14通りが答えとなります。
(2)
でも同様の操作で七角形⇒八角形と調べていく方針となります。
合否を分けた一題
2021年度は難易度に大きな変化は見られませんでした。大半は、受験生にとって一度は見たことのある問題で構成されていたと思われます。ミスなく、手早く問題を処理していく必要があります。
受験生の間で差がつく可能性があるのは、解法によって取り組む時間に差が生じる大問[3](1)計算が煩雑であった(4)(5)、2者間グラフを適切に手早く処理できたかで差が生まれる大問[4]です。この中から、合否を分けた一題として大問[4]を取り上げます。
問題で与えられているのが以下のグラフです。
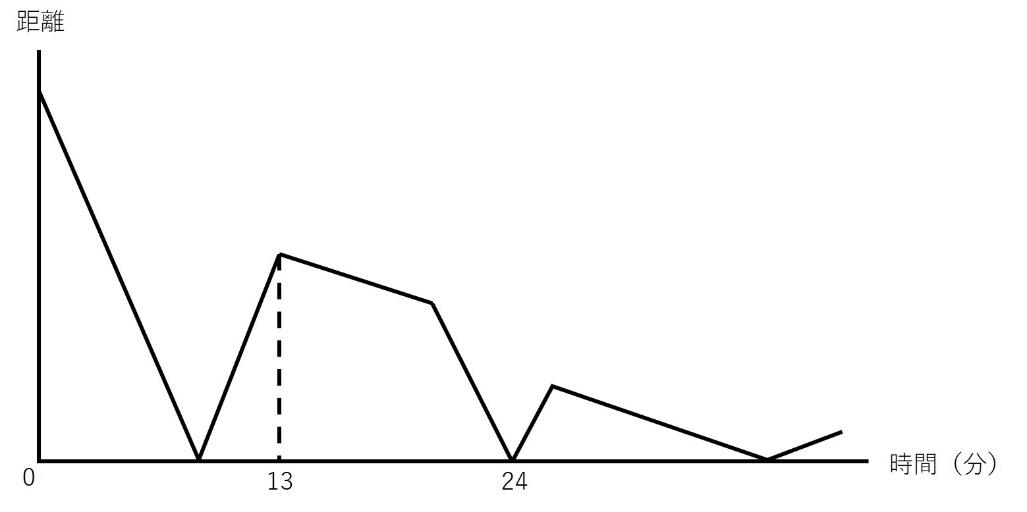
グラフが変化した点において、何が起こったのかを書いておきます。
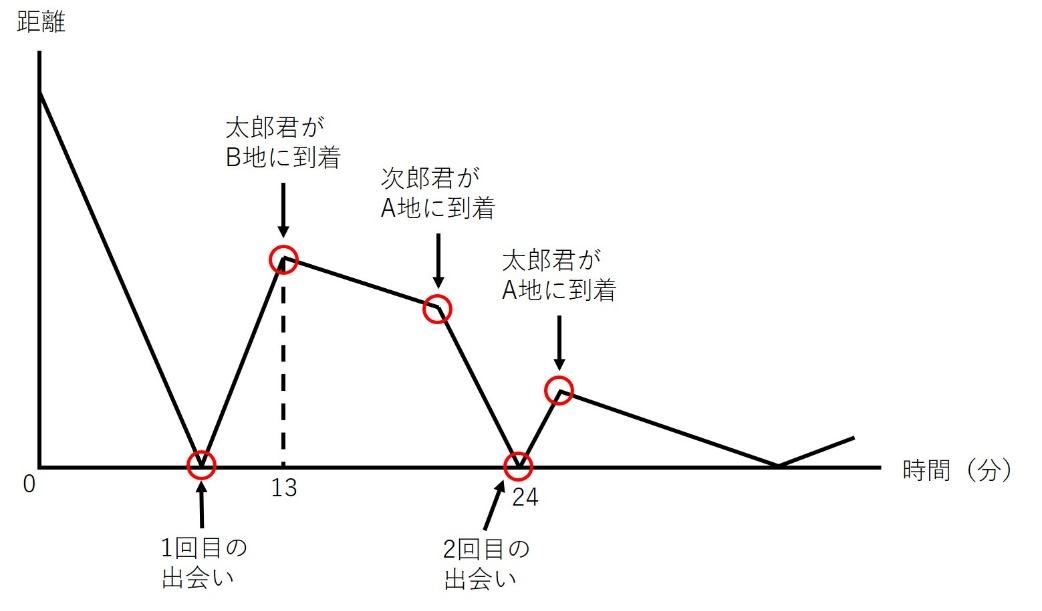
さて、状況についてまとめておきます。
1. 太郎君と次郎君は、異なる地点から向かい合ってスタート
2. 2回目に出会うのにかかる時間は24分
3. 太郎君は片道を13分で移動
以上の条件をもとに、問題に取り組みます。
(1)
1回目の出会いと2回目の出会いを線分図にまとめます。
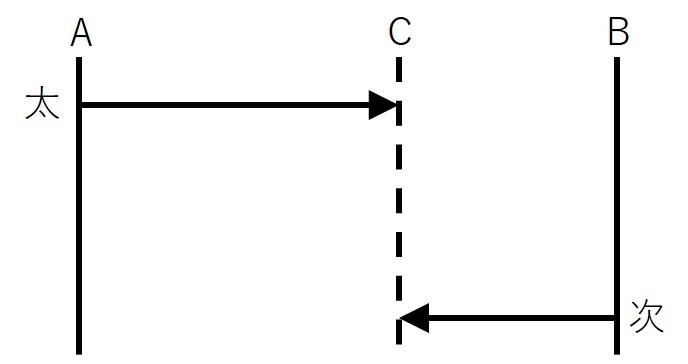
1回目に2人が出会うためには太郎と次郎が合わせてAB間1本分の距離を移動する必要があります。
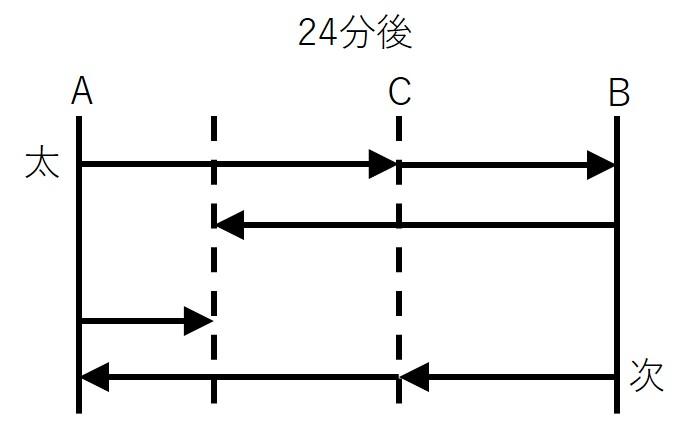
2回目に2人が出会うとき、太郎と次郎は合わせてAB間3本分の距離を移動しています。
AB間3本分移動するのに24分間かかっているわけですから、1本分進むのにかかる時間は
24÷3=8分
とわかります。
また、太郎君がB地にたどり着くまでの様子を図にすると以下のようになります。
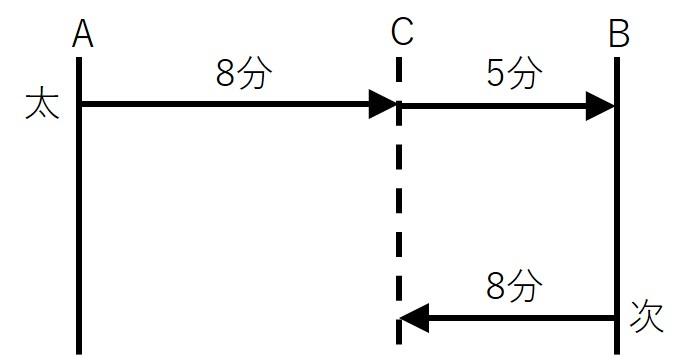
BC間に注目します。
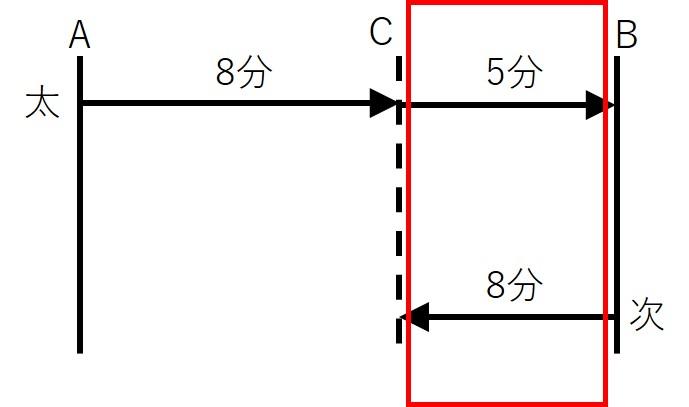
BC間を進むのに、太郎君は5分、次郎君は8分かかっています。よって、同じ距離を進むのにかかる時間の比は、太郎君と次郎君で5:8となります。よって、次郎君がCからAに進むのにかかる時間は
8分×=20..jpg8分
となります。
(2)
同じ距離を進むのにかかる時間の比が5:8ですから、速さの比は8:5となります。太郎君の速さを⑧、次郎君の速さを⑤とおくと、AB間の距離は
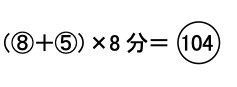
となります。
さて、今回の問題のようにスタート地点が異なり、向かい合って進む状況で「1人がもう1人に追いつく」とは、以下のような線分図で捉えることが出来ます。
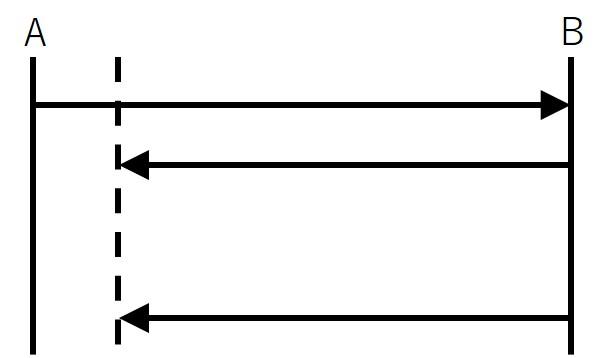
2人の移動した距離の差が、AB間1本分になっています。
よって
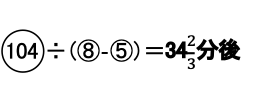
となります。
慶應中等部入試対策・関連記事一覧
慶應中等部入試対策・同じ教科(算数)の記事
- 算数の出題傾向分析
- 算数の合格戦略の提案
- 算数の合否を分けた一題(2011年度)
- 時期による算数の学習法の提案(5年生)
- 時期による算数の学習法の提案(6年生)夏休みまで
- 時期による算数の学習法の提案(6年生)秋以降
- 塾ごとの算数の学習法の提案(サピックス生)
- 塾ごとの算数の学習法の提案(日能研生)
- 塾ごとの算数の学習法の提案(四谷大塚生)
- 算数担当講師から慶應中等部入学を目指す受験生へのアドバイス
- 算数の合否を分けた一題(2013年度)
- 算数の合否を分けた一題(2014年度)
- 算数の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2020年度)
慶應中等部入試対策・同じテーマ(合否を分けた一題)の記事
- 理科の合否を分けた一題(2010年度)
- 算数の合否を分けた一題(2011年度)
- 国語の合否を分けた一題(2011年度)
- 社会の合否を分けた一題(2011年度)
- 国語の合否を分けた一題(2012年度)
- 理科の合否を分けた一題(2012年度)
- 理科の合否を分けた一題(2011年度)
- 算数の合否を分けた一題(2013年度)
- 国語の合否を分けた一題(2013年度)
- 理科の合否を分けた一題(2013年度)
- 社会の合否を分けた一題(2013年度)
- 算数の合否を分けた一題(2015年度)
- 社会の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2016年度)
- 国語の合否を分けた一題(2016年度)
- 理科の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2017年度)
- 社会の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2017年度)
- 国語の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2018年度)
- 国語の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2019年度)
- 理科の合否を分けた一題(2019年度)
- 国語の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2020年度)
- 理科の合否を分けた一題(2020年度)
- 社会の合否を分けた一題(2020年度)
- 理科の合否を分けた一題(2021年度)
- 社会の合否を分けた一題(2021年度)
- 国語の合否を分けた一題(2021年度)