算数の合否を分けた一題（2015年度）

算数の合否を分けた一題

慶應中等部入試対策・算数の合否を分けた一題（2015年度）

難易度分類

大問１	（1）Ａ　　（2）Ａ　　（3）Ａ　　（4）Ａ
大問２	（1）Ａ　　（2）Ａ　　（3）Ａ　　（4）Ａ
大問３	（1）Ａ　　（2）Ａ　　（3）Ａ　　（4）Ａ
大問４	（1）Ａ　　（2）B
大問５	（1）Ａ　　（2）B
大問６	（1）Ａ　　（2）B
大問７	（1）Ｂ　　（2）Ｃ

Ａ：慶応中等部を目指すなら落とすことの出来ない問題
Ｂ：着眼点や解法ツールにより正答率・かかる時間に差がつく問題
Ｃ：難易度や処理量から判断して５分以内に解き切る腕力がなければ後に回すべき問題

問題別寸評

［１］計算問題

冒頭の［１］の計算問題、特筆すべき点はありません。ミスなくしっかりと。

［２］一行題

(１)相当算です。線分図を書くまでもありません。

(２)速さと比、歩幅に関する典型問題。歩幅と歩数の掛け算が速さ比となります。

(３)年齢算です。冒頭の２歳年上という条件は後回し。後半から解いてゆきましょう。
子供：父の比が最初1：２から、5年後２：３に変化したと捉えれば、あとは消去算でも比例式でもOK。

(４)差集め算。最後の1人だけ7個はあげられないという条件は、最後の１人は0～6個と考えましょう。

［３］図形の集合問題

（１）正三角形2つによって正方形の右下の直角が３等分されていることに気づけば終わりです。

(２)「45,45,90度」の三角定規の利用です。三角形ABDの面積は4×2÷2=4㎠となります。

(３)四分円であることを考えると一辺を2とおくのが良いですね。
正方形は2×2=4、扇形は2×2×3.14÷4=3.14
色のついていない部分は4－3.14=0.86となります。

(４)回転体は解き方の手順化がしっかりなされているかで、解答時間に大きく差がつきます。
表面積がドーナツ型＋円柱の側面＋円すい台の側面。ここでえーっとペンが迷っているようではダメです。面積が3.14「いくつ分か」を素早く正確に求めてゆきましょう。(以下3.14略)
ドーナツ型は4×4－1×1=15、円柱の側面は8×4=32
円すい台の側面は母線がの円すいから、母線がの円すいを引くと考え
×4－×1=25
まとめて(15＋32＋25)×3.14=72×3.14=226.08㎠

［４］数の性質

［４］数の性質から約束記号の出題です。(１)を通して〈x,y〉=xとyの積であることを読み取りましょう。
(２)〈〈2,8〉〈15,28〉〉=2×8×15×28となりますが、計算しないこと。
2×8×15×28=42×□にあてはまる□を求めます。
比を簡単にする容量で左辺と右辺割ってゆくと□=160

［５］速さはダイヤグラムを利用する問題

①ダイヤグラムは図形を利用し解く意識、②ダイヤグラムに書かれていないときは延長して描くというテクニックを心得ておく必要があります。

(１)グラフより上りは2.5時間、下りは1.5時間かかったことがわかりますので、それぞれ速さは上りが時速12km、下りが時速20km。清水の速さは上りと下りの平均で時速16kmとなります。

(２)この問題で問われているのは４度目は、ダイヤグラムには３度目まで描かれていますので、伸ばして作図します。するとどちらの船も17時30分にA町、B町についたことがわかります。
あとは砂時計型の相似を利用するも良し、２隻の船が出会うまでの時間を求め17時30分からさかのぼるも良しです。分数計算となりますが、慌てず、冷静に。

［６］場合の数

計算ではなく「書き出しで解く」解法へ頭を切り替えることができたかどうかで明暗が別れる問題でした。合否を分けた1題として後述します。

［７］立体上での点の移動

まずどの点がどの向きに回っているか、速さはいくつかなど、条件を正確に整理すること。出会うのはどの辺上になるかを考え、辺を通過する時間を書き出して考える解法を知っていたかがポイントです。
(１)点PとQが出会うのは辺AE上です。点PとQが辺AE上にいる時間をそれぞれ書き出すと
点P　10～12,22～24,34～36,46～48,58～60
点Q　9～10,19～20,29～30,39～40,49～50,59～60
59～60秒で出会うことがわかります。出会った後、点PはAに、点QはEに同時に着くことを利用し、２点が辺AEで出会うまでの時間を、60秒から引き算して求めましょう。

(２)３つの点ですが、点Rは点Pの２倍細かい周期で進んでいるだけですので、点Pと点Qのみ調べればOK。

合否を分けた一題

昨年よりも難易度は低く、処理速度と的確さ、加えて解法知識の広さが問われる出題となりました。中でも骨のある出題が目立つ場合の数からは、かく乱順列が出題され、そこで書き出しという判断が素早くできたかどうかが、合否の分かれ目のひとつだったと言えるでしょう。
では、２０１５年度の合否を分けた一題として、その［６］（２）を取り上げます。

［６］（２）

十の位の数が全て異なるという条件から、４つの数は
1□、2□、3□、4□となります。
この□にそれぞれの十の位と異なる数字を入れるのですから、
1□には1以外、2□には2以外…つまりかく乱順列ということになります。
数の少ないかく乱順列は書き出しが最も有効です。
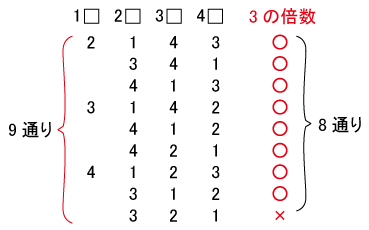
特にこの問題の場合、イで3の倍数が含まれるものが問われていますので
書き出して3の倍数も判定するのが得策です。
書き出すと以下の様にアは9通り、イは8通りとなります。