算数の合否を分けた一題
慶應中等部入試対策・算数の合否を分けた一題(2011年度)
2011年度(H23年度)入試 難易度分類
[1](1)A (2)A (3)A (4)B
[2](1)A (2)A (3)A (4)A
[3](1)A (2)A
[4](1)A (2)B
[5](1)A (2)A
[6](1)A (2)B
[7](1)A (2)B
A:中等部合格を目指すなら必ず得点したい問題
B:着眼点や解法ツールにより正答率・所要時間に差がつく問題
C:難易度や処理量から判断して、3分以内に解き切る腕力がなければ一旦とばすべき問題
2011年度(H23年度)の入試問題は、所々に受験生の手を止めるような問題が配置されているものの、全体としては非常に解きやすいセットです。
[1](4)や[2](2)~(4)の一行問題については、「何回も解いた経験があるけれど、結局苦手なままで本番をむかえてしまった受験生」が少なからずいたでしょう。解けない問題・苦手な問題のつぶしこみを日頃からコツコツ取り組む努力の必要性を認識させてくれます。
受験生の手を止めた問題は[4](2)・[6](2)・[7](2)の3題。
まず[4](2)は「3回目から8回目までの得点の平均」をどうとらえたかがカギ。例えば「3回目から8回目の6回分のうち、A君が10・20で、B君が10・20・40・50」のとき、正しくは「A君の平均は(10+20)÷6=5点、B君の平均は(10+20+40+50)÷6=20点」と考えるべきところを、「A君の平均は(10+20)÷2=15点、B君の平均は(10+20+30+40)÷4=30点」と考えてしまった受験生、もしくはどちらが正しい計算方法なのか悩んだ受験生は、ここで痛い失点をしたでしょう。
次に[7](2)は水の深さを求める問題ですが、「水」ではなく「空気」に注目できたかがカギ。どちらも三角形の相似を利用して必要な部分の長さを求めていきますが、「空気」に注目できた受験生は所要時間が短縮できたはずです。
最後に[6](2)は、思考力問題として解いた経験のある受験生が多かったのでは。他校の入試問題でもよく見かけるタイプのサイコロ問題です。今回はこの[6](2)を取り上げます。
[6]サイコロは向かい合う面の数の和が7になるように作られています。いま、下の図と同じサイコロをいくつか使って立体を作ります。このとき、サイコロがぴったり合わさっている面の数の和も7になるようにします。次の[ ]に適当な数を入れなさい。
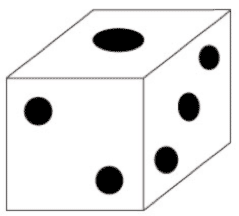
(2)[図2]で床に接しているサイコロの面の数の和は[ ]です。
慶應中等部入試対策・関連記事一覧
慶應中等部入試対策・同じ教科(算数)の記事
- 算数の出題傾向分析
- 算数の合格戦略の提案
- 時期による算数の学習法の提案(5年生)
- 時期による算数の学習法の提案(6年生)夏休みまで
- 時期による算数の学習法の提案(6年生)秋以降
- 塾ごとの算数の学習法の提案(サピックス生)
- 塾ごとの算数の学習法の提案(日能研生)
- 塾ごとの算数の学習法の提案(四谷大塚生)
- 算数担当講師から慶應中等部入学を目指す受験生へのアドバイス
- 算数の合否を分けた一題(2013年度)
- 算数の合否を分けた一題(2014年度)
- 算数の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2020年度)
- 算数の合否を分けた一題(2021年度)
慶應中等部入試対策・同じテーマ(合否を分けた一題)の記事
- 理科の合否を分けた一題(2010年度)
- 国語の合否を分けた一題(2011年度)
- 社会の合否を分けた一題(2011年度)
- 国語の合否を分けた一題(2012年度)
- 理科の合否を分けた一題(2012年度)
- 理科の合否を分けた一題(2011年度)
- 算数の合否を分けた一題(2013年度)
- 国語の合否を分けた一題(2013年度)
- 理科の合否を分けた一題(2013年度)
- 社会の合否を分けた一題(2013年度)
- 算数の合否を分けた一題(2015年度)
- 社会の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2016年度)
- 国語の合否を分けた一題(2016年度)
- 理科の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2017年度)
- 社会の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2017年度)
- 国語の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2018年度)
- 国語の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2019年度)
- 理科の合否を分けた一題(2019年度)
- 国語の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2020年度)
- 理科の合否を分けた一題(2020年度)
- 社会の合否を分けた一題(2020年度)
- 算数の合否を分けた一題(2021年度)
- 理科の合否を分けた一題(2021年度)
- 社会の合否を分けた一題(2021年度)
- 国語の合否を分けた一題(2021年度)