算数の合否を分けた一題
筑波附属中入試対策・算数の合否を分けた一題(2020年度)
難易度分類
| 1 | (1)A (2)A (3)A (4)A (5)A (6)A (7)A |
|---|---|
| 2 | A |
| 3 | (1)B (2)A |
| 4 | (1)A (2)A |
| 5 | (1)B (2)B |
| 6 | C |
| 7 | A |
| 8 | A |
| 9 | B |
| 10 | (1)A (2)A |
A…筑波大附属中学校合格を目指すなら、確実に得点したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難易度、処理量から判断して、部分点を拾えれば良しとする問題
出題総評
出題傾向や問題数ともに例年通りでした。全体的に、直近3年の過去問に類題がある問題が多く出題されていました。
各問題の解説の前に、直近3年の過去問から類題となっている問題の年度と番号を記載しておきました。参考にしてください。
筑波大付属中学の算数入試は、社会と合わせて50分という時間の短さも特徴の一つです。過去問での学習をじっくりと行い、テンポよく解き進められるようにしたいです。
2020年度 問題別寸評
計算問題と小問集合です。時間の消費を抑えられるかどうかが鍵となります。
(1)
小数の計算問題です。3.4と34でまとめる計算の工夫をする必要があります。
(2)
「連続する~個の整数の和」という問題です。「最も小さい数を求めなさい」の指定を読み落とさないようにしましょう。
(3)
カードを並べ、整数をつくる問題です。典型題は、「2の倍数」や「3の倍数」を問う問題で、計算で求めますが、本問は「素数」の数を問うています。書き出すと短時間で答えを出せます。「この問題は書き出せば解ける」と判断するまでの時間を短くできるように練習しておきましょう。
(4)
分母を50にそろえて考える方法を用います。分母を50にそろえ、分子が18.75と、33.33333……になることから、19以上33以下の整数で、かつ50と互いに素な整数を数え上げます。
(5)・(6)
どちらも約数・倍数の単元の基本問題です。特に悩むことなく、解法が浮かぶと良いでしょう。
(7)
食塩水の問題です。典型題ではありますが、比較的珍しい状況設定です。水100g、食塩20gを溶かした食塩水の濃度を”100″ /”6″ %とし、食塩の濃度を100%として計算をすると考えやすいでしょう。
規則性・群数列の問題です。
数列の規則は1,1,2,3,4,/2,2,3,4,5/3,3,4,5,6/……
のように、数字5個ずつの周期となっています。
また本問では、奇数の個数に着目しています。そのため、各グループ内に含まれる奇数の個数に規則がないかと予想します。
以下のような表を書いて、規則がないか調べてみます。

すると、奇数の個数が3・2・3・2……のよう規則的に並んでいることが分かります。
999÷5=199 あまり4
199×2=398 より、398組目まで並べ、さらに奇数が4個出るまで並べます。
次の399組目には奇数が3個含まれていますので、左から999個目の奇数は、400組の1個目の奇数であることが分かりました。
400組の1個目の奇数は、400組の3番目にありますので、答えは
399×5+3=1998 となります。
平面図形の問題です。
(1)
問題文の指定である「正方形の紙を対角線で切り、対角線が平行になるように重ね合わせました」という文章と図との関係が理解できれば、後は比較的簡単な問題だったでしょう。
(2)
角度の問題です。正三角形を半分に切ったことから、30°,60°,90°の三角形であることを利用し、丁寧に三角形の内角の和と対頂角を利用して角度を追っていけば答えに辿り着けるでしょう。
(1)
面積比が2:3であることから、上底と下底の長さの和も2:3になることを利用します。
(2)
容器に水を入れる問題で、底面積の比を利用する問題です。
2019年の大問4や、2017年の大問4に類題が出題されています。
Aの容器で12㎝分の水をBの容器に入れると、水位が9㎝上昇したことから、AとBの容器の底面積の比を求めます。
こちらも特に解法に悩むことなく解いておきたい問題です。
平面図形の相似・割合を用いた問題です。
2019年の大問10や、2017年の大問8に類題が出題されています。
(1)
問題の図形を見た際に「どこかで見たことあるな」と思ってほしい問題です。相似を利用して辺の長さの比を求め、そこから解いていきます。過去問に類題が出題されているので、筑波大附属中学の受験生ならば解けてほしい問題です。
(2)
平行四辺形の種類と個数を数え上げる問題。数え上げ問題では、どのように場合分けするかが勝負のカギとなります。見つけた順にバラバラと数えていくのでは、数え漏れが発生してしまいます。この場合は、平行線の組み合わせに注目して場合分けするのが良いでしょう。
合否を分けた一題で取り上げます。
立方体を積み上げた図形の問題です。気づきにくかったかもしれませんが、本問は投影図と関係が深い問題です。
投影図に関する出題としては、2019年の大問8や、2017年の大問6などがあります。投影図は近年頻出ですので、抑えておきましょう。
問題文には「木の枠を通り抜けることが出来る」とありますが、つまり、投影図を描いたときに同じ形になるものを選べ、という問題に帰着させることが出来ます。
立方体の展開図に矢印が書かれており、組み立てた際の見え方を問う問題です。類題として展開図に関する問題は、2019年の大問9や、2018年の大問10があります。
さて、問題で示されている図を見ると、矢印の位置が離れていて、関係性をつかみにくくなっています。このような時は、展開図の付け替えをすると良いです。
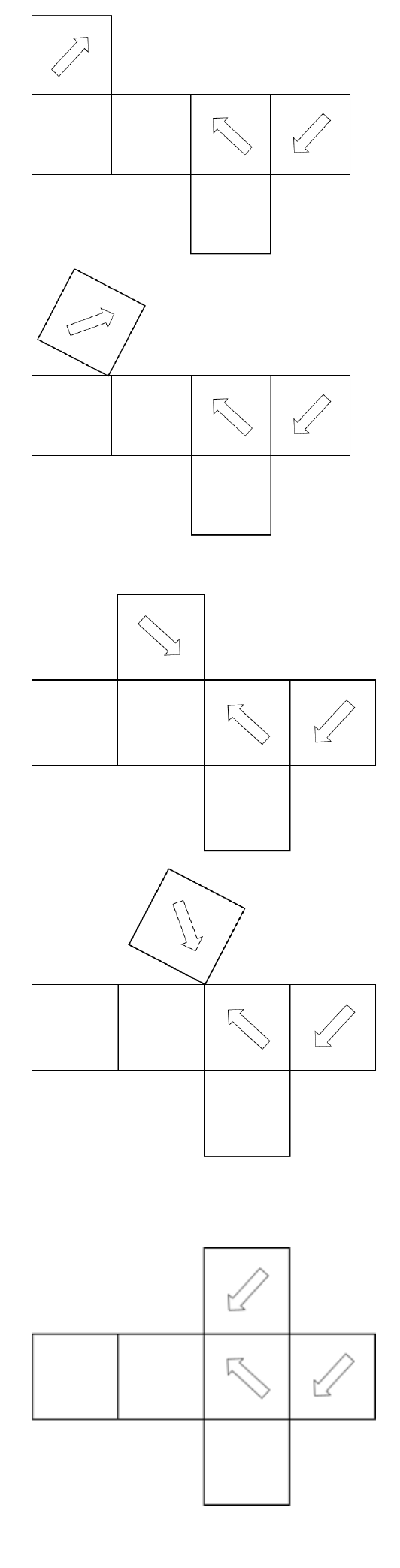
上の図のように、展開図をパタパタとつけかえることで、矢印が描かれている正方形同士を近づけていきます。
この考え方は、展開図の様々な問題に応用できますので、ぜひ身に着けておくと良いでしょう。
ボールのはね上がりと□を使った式がテーマとなっている問題です。
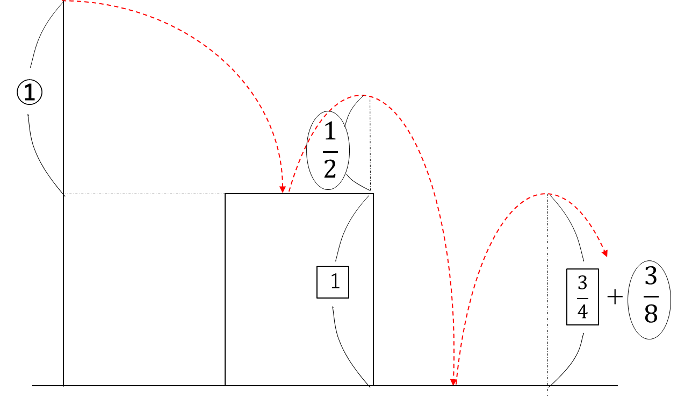
通常のボールのはね上がりの問題は、最初に落とすときの高さを①のように設定すると解ける問題が多いです。しかし今回は、箱の高さも分からない、という点がポイントです。
図のように、落とした位置から箱までの高さを①とし、箱の高さを1とします。すると、はね上がりの高さは図のようになります。
最後に、はね上がった高さが箱の高さと同じであることを利用して、消去算のように解いていきます。
旅人算の問題は本学で頻出のテーマです。しかし、今回のグラフは見慣れない形式だったかもしれません。ダイヤグラムではないので、このグラフだけを見ていては、人が動いている様子を掴むことは難しいでしょう。
グラフから速さの変化についての情報を読み取り、そのうえで線分図を描いて状況を把握するのが良いです。
ケンタさんは、9時から9時40分までの40分間で7㎞移動しています。グラフには9時25分までの情報が示されています。9時25分から9時40分までに移動した距離の合計を求めるため、まずは9時から9時25分までに移動した距離の和を計算していきます。
150×10+300×10+200×5=5500m
7000-5500=1500m
9時25分から9時40分までの15分間で移動した距離が1500mなので、その間の速さは
1500÷15=100 より、分速100mとなります。
ケンタさんと兄の出発時刻がずれているので、まずはこの点を処理していきます。
9時10分の時点で、ケンタさんと兄が何m離れているかを計算してみます。
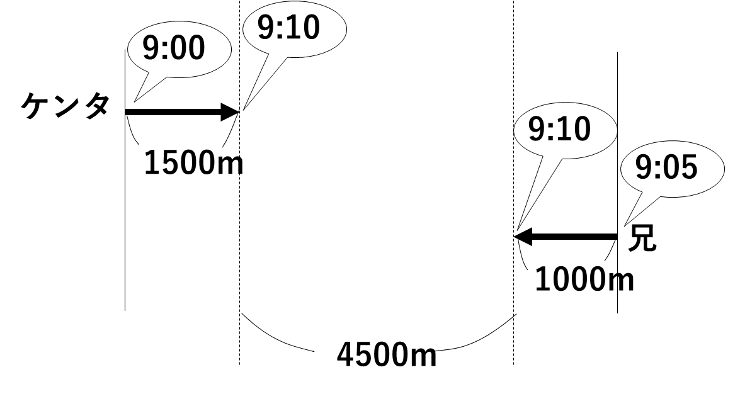
すると、ケンタと兄は4500m離れていることがわかります。9:10~9:20は、ケンタは分速300、兄は分速200mで進みます。よって、もし9:10~9:20の間に二人がすれちがうとしたら、4500を、二人の速さの和である200+300=500で割り算することで時刻を求めることができます。
4500÷(200+300)=9分
計算結果が10よりも小さくなりましたので、9:10の9分後にすれ違うことがわかりました。
よって答えは、9:19です。
筑波大付属中学の算数は、直近数年の過去問に非常によく似た問題が出題されます。
過去問をやりこむことは当然として、その上で更に、塾のテキストなどで類似した切り口の問題が出ている際には、特に注目して学習を進めると良いです。
そのためにも、6年生の早い段階で、大まかな傾向については知っていた方がよいかもしれません。
どのような問題が出題されやすいのか知っていれば、普段の学習の際にもより一層真剣に取り組めるでしょう。
また、展開図に関する問題の解法テクニックなどは、通常の塾の授業ではそれほど力を入れて解説されない傾向にあります。
個々のセンスに頼った指導がなされがちですが、突き詰めていけば効果的な対策は存在します。筑波大付属中学の傾向を熟知し、その対策が出来るようにしましょう。
合否を分けた一題
紙を折り返して切り落とす問題です。類題としては2018年の大問8に、円形の紙を何度も折って切る問題が出題されています。
実際に紙を切ることなく、切断の様子をイメージするにはどのようにしたら良いでしょうか。紙を折り返した様子を立体的に作図出来ればそれでも良いですが、非常に難しいです。ここでは、平面上で、折り返しの様子、切断の様子を追うための方法をご紹介します。
手順は二つあります
①折り目の線を書き入れる
②切れ込みの線を書き入れる
です。具体的に解説していきます。
まず、1回折ってから切った際の様子を例にとります。
1回折ったとき、折り目の線は下図のようになります(青い線が折り目です)。

次に、切り口の線は下図のようになります(赤い線が切り口です)。

よって、下図の赤い部分が切り落とされます。

このように、まず折り目がどこに付くかを考えて図に書き入れ、そのあとで、ハサミがどこを切るのかを図に書き入れていきます。
この考え方を基に、5回折った時の様子を図示していきます。
折り目の線は、下図のようになります。

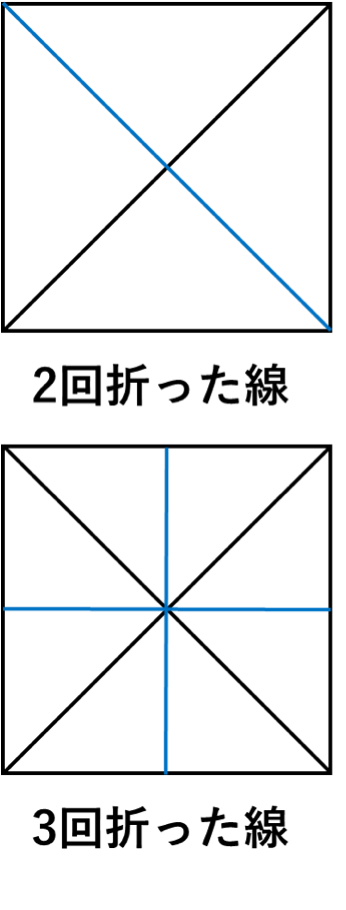
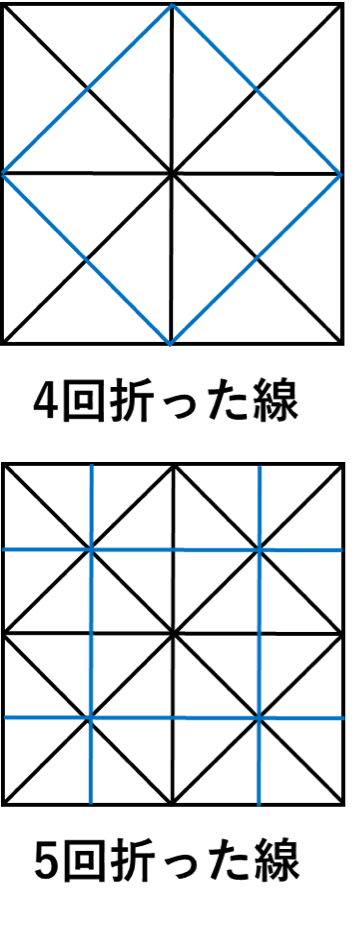
次にこの線に、切込みの線(ハサミが切る線)を書き入れていきます。

上の図のようになります。どこに赤い線を引けばよいかの基準としては

上の図のように、直角三角形の、この位置関係に全て線を引くようにします。
よって、直角に等辺三角形8枚、正方形4枚、くりぬかれたフチ1枚に分かれるので、答えは13枚です。
立体図形の複雑な問題は、できるだけ平面化して考えることが基本です。
頭の中で立体の複雑な動きをイメージすることは非常に難しいです。
そのような能力には頼らず、誰でもできるように、立体を平面化するテクニックを身につけることが大切です。
筑波附属中入試対策・関連記事一覧
筑波附属中入試対策・同じ教科(算数)の記事
筑波附属中入試対策・同じテーマ(合否を分けた一題)の記事
- 算数の合否を分けた一題(2016年度)
- 国語の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2017年度)
- 国語の合否を分けた一題(2017年度)
- 社会の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2018年度)
- 国語の合否を分けた一題(2018年度)
- 理科の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2018年度)
- 理科の合否を分けた一題(2019年度)
- 国語の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2021年度)
- 社会の合否を分けた一題(2021年度)
- 理科の合否を分けた一題(2021年度)


 (3 votes, average: 3.67 out of 5)
(3 votes, average: 3.67 out of 5)