算数の合否を分けた一題（2019年度）

算数の合否を分けた一題

豊島岡女子中入試対策・算数の合否を分けた一題（2019年度）

難易度分類

［１］	(1)A　(2)A　(3)A　(4)A
［２］	(1)A　(2)B　(3)A　(4)C
［３］	(1)A　(2)B
［４］	(1)A　(2)C
［５］	(1)A　(2)A (3)B
［６］	(1)A　(2)B　(3)C

Ａ：豊島岡合格を目指すなら必ず得点したい問題
Ｂ：着眼点や解法ツールにより正答率・かかる時間に差がつく問題
Ｃ：難易度や処理量から判断して、部分点狙いで答案を作成すべき、もしくはとばすべき問題

出題総評

今年も、大問１・２は計算および各単元からの小問集合が計８問、大問３～６は４つの単元にわかれて、という昨今の形式が踏襲された入試となりました。
詳細については大問１が計算１問＋小問３問（場合の数・割合・数の性質）、大問２は文章題が３問と平面図形が１問、大問３は規則性の問題、大問４は２点の移動の問題、大問５は場合の数の問題、大問６は立体図形の応用問題でした。

問題別寸評

［１］

(1)　答　７．６
分数や小数の混合計算。工夫は特にないので、分数に統一して慎重に・順番に計算していきましょう。

(2)　答　１０個
カードを並べる場合の数の、典型的な一行問題。偶数なので、一の位は使えるカードのうち０か２です。０の場合は百の位、十の位、一の位と３×２×１＝６個、２の場合は２×２×１＝４個できます。（４種類の数字、ではなく４つの数字ということにも注意しましょう）

(4)　答　２１１９
～でわると～あまる、という倍数の典型問題。余りがバラバラ→不足数もバラバラなので、両方の条件に合うものを書き出して重なるところを調べます。
１１で割ると７余る→７、１８、２９、４０、５１、６２、７３…
３１で割ると１１余る→１１、４２、７３…
となり、最小は７３です。その次は、割った数である１１と３１の最小公倍数＝３４１ずつを足していくことになり、式に表すと７３＋３４１×□＝１９５０にもっとも近い数、おちうことになり答えが求まります。

［２］

(1)　答　３１枚
和と差の文章題で、差集算の問題です。
合計金額が６２円切手で８２円切手よりも１０３０円少ないといっていますが、８２円切手が６２円切手よりも５枚多いことから、両方とも枚数を６２円切手にそろえると、８２×５＝４１０円分の差が縮まることとなり、１０３０－４１０＝６２０円の差になります。１枚当たりの差が８２－６２＝２０円なので、ここから答えが求まります。

(2)　答　５時間

(3)　答　A２６個、B１４個

(4)　答　１６４０㎡
３頭の牛の動ける範囲を考える平面図形の問題。それぞれの牛が互いに重なり合うところ・そうでないところをしっかり作図して捉える必要があり、かなりの難問です。各々の牛が動ける範囲を作図すると以下のようになります。

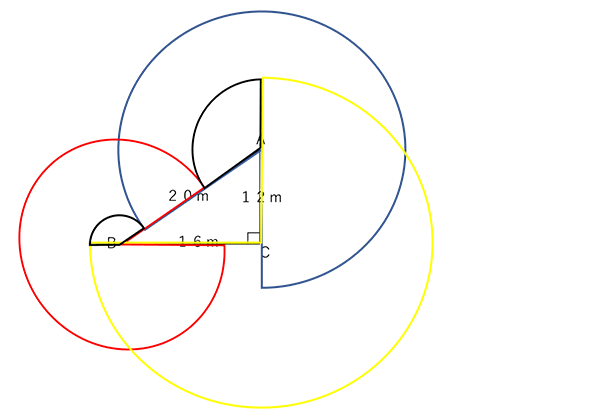
続いて、Aの牛（つな１６ｍ）とBの牛（つな１２ｍ）がぎりぎりで重なるところを考えると、上図の青い円弧と赤い円弧が交わる部分になります。（下図の太い点線の部分）

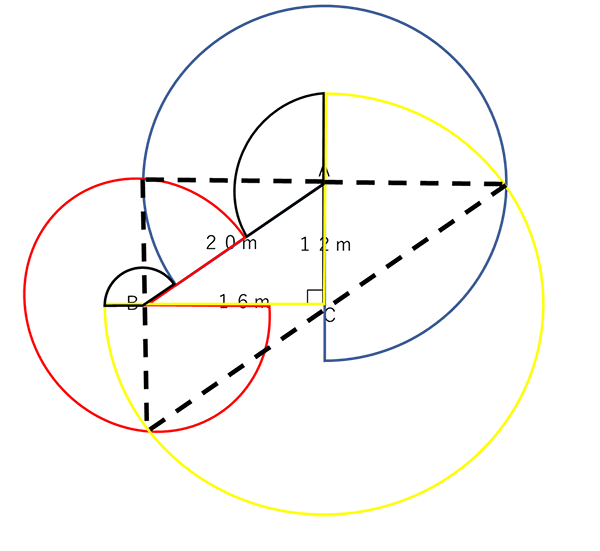
同様にＡとＣ、ＢとＣで同じように考えると以下のようになります。

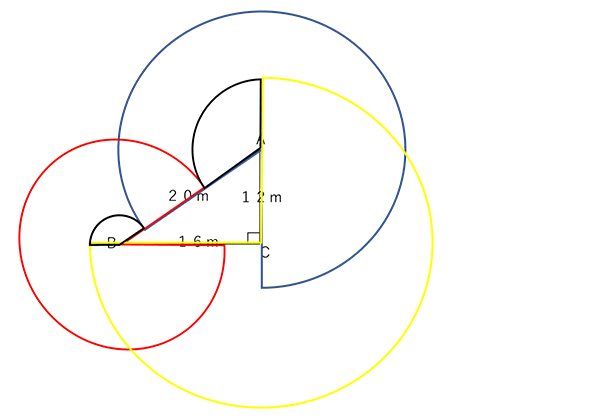
よって、牛が動ける部分の面積の合計は以下のような半径が１２ｍ、１６ｍ、２０ｍの半円の面積と、縦が１２×２＝２４ｍ・横が１６×２＝３２ｍの直角三角形の面積の合計となります。

［３］

ここからは大問になります。５の倍数を並べた数列をテーマにした規則性の問題。
(1)　答　５
７で割った…とあるので、５と７の倍数の最小公倍数である３５までを１周期として考えます。５、１０、１５、２０、２５、３０、３５までを７で割ったときの余りはそれぞれ５、３、１、６、４、２、０となり、この７個の数字の繰り返しが４０以降の５の倍数でも続いていくことになります。１２７番目なので１２７÷７＝１８グループ…１となり、余りから答えが求まります。

(2)　答　５７５１
さきほどと同じように、５～３５、４０～７０…と３５を１周期として考えます。５、１０、１５、２０、２５、３０、３５までを７で割ったときの商はそれぞれ０、１、２、２、３、４、５で合計は１７です。次に４０、４５、５０、５５、６０、６５、７０までを７で割ったときの商はそれぞれ５、６、７、７、８、９、１０で合計は５２です。なお、１周期が３５なのでそれぞれの商は３５÷７＝５増えるため、１７＋５×７＝５２としても構いません（例えば、７で割ったときの商は５→０、４０→５で５増えている）。ここから、この数列の１～７番目までの和は１７、８～１４番目までの和は５２、１５～２１番目までの和は８７（＝５２＋３５）…と３５ずつ増えていくことがわかります。１２７番目を問われており、１２７÷７＝１８…１なので１２７－１＝１２６、１２０～１２６番目までの和を考えます。下線を引いた部分が７の倍数となっていることに着目すると、７＝７×１、１２６＝７×１８なので１２０～１２６番目までの和は１７＋３５×（１８－１）＝６１２です。したがって、１～１２６番目までの和は１７＋５２＋８７＋…＋６１２＝（１７＋６１２）×１８÷２＝５６６１です。１２７番目の数については、数列上で１番目の数→０、８番目の数→５、１５番目の数→１０となっており、番目が７増えるごとに数が５増えていきます。（１２７－１）÷７＝１８、０＋５×１８＝９０とわかります。先程計算したものと合わせれば答えが求まります。

［４］

２点が動き、そうしてできた三角形と台形の面積の大小を考えていく点の移動と平面図形（相似）の問題。
(1)　答　図形イの方が１２㎠大きい
実際に１２秒後の様子を作図すると以下のようになります。

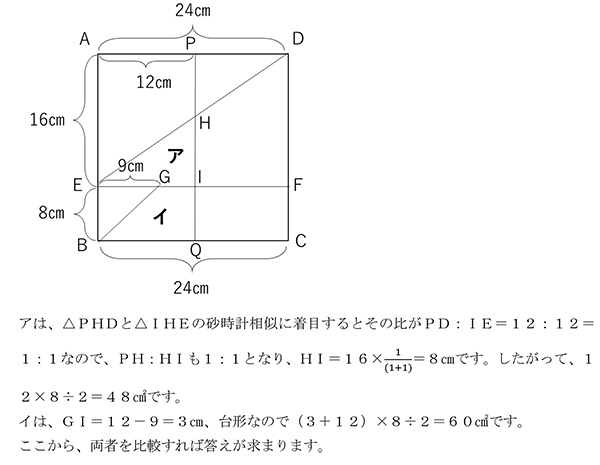
(2)　答　１８秒後
(1)の１２秒後と比較しながら、図形アと図形イの各々の面積について考えていかなければならない難問です。まずは本問で考えなくはならない情況について作図してみます。

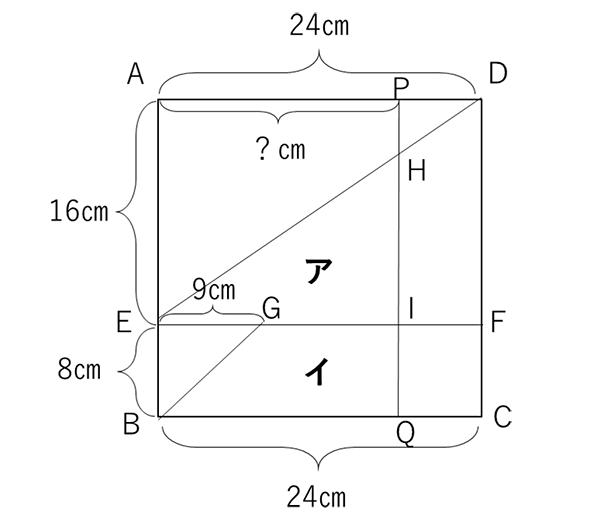
次に、図形イを下図のように２つの三角形にわけてみると、△ＧＩＱの面積が（１２－９）×８÷２＝１２㎠となり、(1)の答えになっていることがわかります。ここから、△ＥＨＩと△ＧＢＱは面積が等しいことになります。

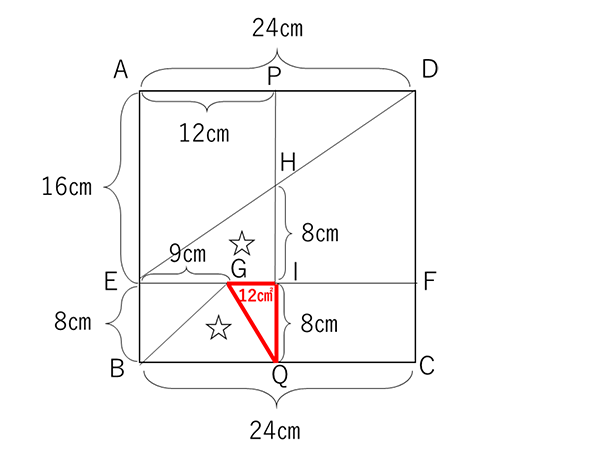
では、この図に最初の図を重ねあわせてみましょう。

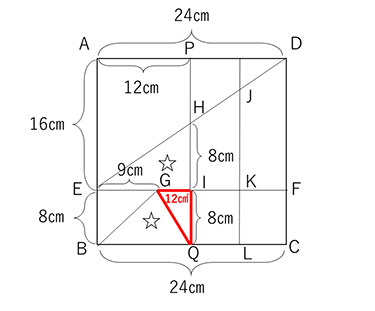
図形ア（△ＥＪＫ）と図形イ（台形ＧＢＬＫ）の面積が同じですが、このうち☆の部分がお互い等しいです。ＨＩ＝ＩＱ＝８㎝であることに着目し、さらに共通部分を探すべくＨからＪＫに向かって垂線を引きます。

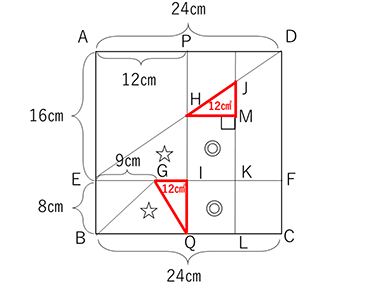
すると長方形ＨＩＫＭも長方形ＩＱＬＫも、縦が共に８㎝・横の長さも等しいので面積が等しいことになります（図の◎の部分）。したがって、残りの部分である△ＨＭＪは、△ＧＩＱと同じで１２㎠ということになります。この三角形は△ＤＥＦと相似で、その比は縦：横＝ＤＦ：ＥＦ＝１６：２４＝２：３です。ＪＭ×ＨＭ÷２＝１２で、ＪＭ：ＨＭ＝２：３になるようなＪＭは４㎝、ＨＭは６㎝だけです。ここから、Ｐ・Ｑが移動した距離がわかり、答えが求まります。（実際にここまでを本番の試験中で考えるのは困難です。(1)の答えである１２秒後から、Ｐ・Ｑが到着する２４秒後までで大体の見当をつけて答えを求める方が現実的でしょう）

［５］

円周上の点を２人がじゃんけんをしながら動いていき、その様子を考えていく場合の数の問題。今年は本問を、合否を分けた一題として後述いたします。
(1) 答　Ｄ
(2) 答　１回
(3) 答　Ｂ、Ｅ、Ｇ

［６］

最後の大問であり、昨今の入試で良くテーマとして扱われる立体図形の問題。水そうを傾けて、水面が立方体のどの点を通るのかイメージが湧きづらい受験生も多くいたと思われます。最終問である(3)は相当な難問と言えるでしょう。
(1) 答　１５１２㎤
真上から見たときにＢＣとＥＨが重なるということは、ＥＨを軸として左の向きに４５°傾けたということです。そのときの水そうを正面から見た図は以下のようになります。

水のある部分の底面積は１２×１２－６×６÷２＝１２６㎠となり、水の体積はこれに高さの１２㎝をかければ求まります。

(2)答　１４４０㎤
ＣとＥを直線で結んだときに、水面を考えた場合にその垂線はＤを通ることになります。作図をすると以下のように、垂線はＧも通ります。（正面から見た図がＣＥを対称軸として線対称になるため）

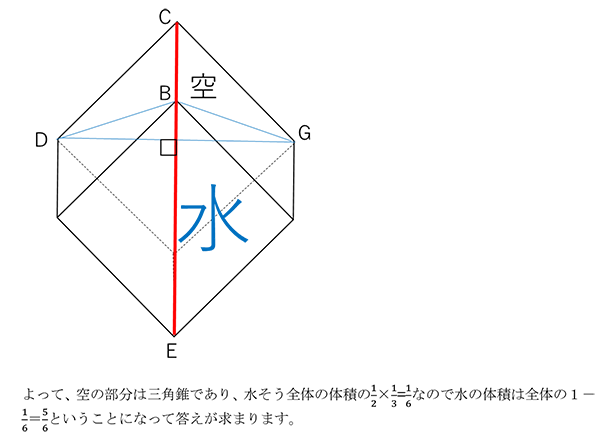
(3) 答　１６０６．５㎤
(2)でDを通ったので、本問でのKを通る場合と比較した図を描いてみます。

合否を分けた一題

今回は、後半の大問群の中で場合の数である大問５について合否をわけた一題として紹介しましょう。決して平易な典型題などではなく、問題文の条件を一つ一つ整理して情況を丁寧に考えていかなければならず、差がついた問題と言えそうです。

［５］場合の数

(1) 花子さんが３回勝ち続けたとしても、右回りに６マス進むのでＨにくることはできません。したがって、３回じゃんけんを終えて合計で左回りに１マス進んだということです。花子さんの場合、勝つと右回りに２マス、負けると左回りに１マス、あいこだと右回りに１マス進むので、例えば（←１、←１、→１）のような場合になります。（１回勝ってしまうと、Ｈまで左に３マスを２回で進むのは不可能です）このとき、花子さんは（負け、負け、あいこ）なので豊子さんは（勝ち、勝ち、あいこ）となり、豊子さんの場合、勝つと左回りに２マス、負けると右回りに１マス、あいこだと左回りに１マス進むので、（←２、←２、←１）と進むのでＤにいることになります。
答え：Ｄ
(2) すべての場合を試験時間内で考えるのは理論的に不可能です。(1)と問題文の条件をよく比較して考えてみると、２人のスタート地点が同じ・じゃんけんをした回数も同じです。さらに、先程では花子さんがＨ、豊子さんがＤにいて４つ離れているということも合致しています。よって、(1)よりあいこは１回です。
答え：１回
(3) １回の勝ち負けで２人は２－１＝１マスだけ離れます。（例えば、２人が同時にＡからスタートしたとして、花子さんが勝って豊子さんが負けた場合は、花子さんはＡから→に２マス、豊子さんはＡから→に１マスで２人は１マスの差がつくということです）１回のあいこで２人は１＋１＝２マスだけ離れます。(1)で３回のじゃんけんが終わった時点で４マス離れていました。全てのじゃんけん後に２人が同じ点にいるということは、全部で２人は１周分＝８マス分離れたことになります。よって、後半３回のじゃんけんで８－４＝４マス分の差がついたことになります。４＝１＋１＋２なので、片方の人のじゃんけんの結果が（勝ち、勝ち、あいこ）（勝ち、負け、あいこ）（負け、負け、あいこ）のどれかであるということです。豊子さんの場合で考えると、
①（勝ち、勝ち、あいこ）のとき…Ｄ→Ｂ→Ｈ→Ｇとなり、Ｇです。
②（勝ち、負け、あいこ）のとき…Ｄ→Ｂ→Ｃ→Ｂとなり、Ｂです。
③（負け、負け、あいこ）のとき…Ｄ→Ｅ→Ｆ→Ｅとなり、Ｅです。
なお、相手の花子さんの場合でそれぞれを考えた場合も、同じ答えとなります。
答え：Ｂ、Ｅ、Ｇ

著者：受験Dr. (受験ドクター)

この記事は役にたちましたか？