算数の合否を分けた一題（2018年度）

算数の合否を分けた一題

豊島岡女子中入試対策・算数の合否を分けた一題（2018年度）

難易度分類

［１］	(1)A　(2)A　(3)A　(4)A
［２］	(1)B　(2)A　(3)A　(4)A
［３］	(1)A　(2)B
［４］	(1)A　(2)B　(3)C
［５］	(1)B　(2)B
［６］	(1)B　(2)B　(3)C

Ａ：豊島岡合格を目指すなら必ず得点したい問題
Ｂ：着眼点や解法ツールにより正答率・かかる時間に差がつく問題
Ｃ：難易度や処理量から判断して、部分点狙いで答案を作成すべき、もしくはとばすべき

出題総評

今年も、大問１・２は計算および各単元からの小問集合が計８問、大問３～６は４つの単元にわかれて、という昨今の形式が踏襲された入試となりました。
詳細については大問１が計算１問＋小問３問、大問２は文章題が３問と平面図形が１問、大問３は場合の数の問題、大問４は２人あるいは３人の動きを追っていく速さの文章題、大問５は比を利用する平面図形の問題、大問６は立体図形と平面図形の応用問題でした。

問題別寸評

［１］

(1)　答　１２３４５

足し・引きの計算問題。工夫は特に考えず、慎重に計算していきましょう。

(2)　答　７個

割合の概念を含んだ、典型的な一行問題。一つ一つ求めるべきものを計算していきましょう。ここでの失点は許されません。

(3)　答　４９５

概数と規則性の問題。もともとの整数の範囲と、等差数列の和の公式を利用すれば答えが求まります。こちらも落とせません。

(4)　答　５個

ある図形の中に、何枚まで図形を並べられるかという問題。正方形の１２㎠は、およそ１辺が３．４㎝（３．４×３．４＝１１．５６㎠）ですので、長方形の横の全長が２０ｃｍということから答えが求まります。

［２］

(1)　答　８問

和と差の文章題。不定方程式と鶴亀算が絡みます。
まず、豊子さんの条件から５×□＋４×△＝５２点となり、あてはまる□と△の組み合わせは８，３か４，１３が考えられます（不定方程式）。
次に、花子さんの条件から失点が１００－６７＝３３点となり、５点の問題と４点の問題を合わせて７問間違えたので５点は５問、４点は２問間違えたことがわかります（鶴亀算）。
ところが、豊子さんが５点の問題を４問すべて正解したとなると、花子さんの５点の問題を５問間違えたという条件が矛盾してしまいますので、残った組み合わせが答えとなります。

(2)　答　６４秒

最小公倍数を利用した周期の典型題。Aは５＋３＝８秒間、Bは４＋８＝１２秒間を１周期とするので、最小公倍数である２４秒後まで〇×を使いながら整理をして調べます。本問は落とせません。

(3)　答　１４％

消去算と割合が絡んだ食塩水の典型題。問題文の２つの条件から、B１００ｇに６ｇの食塩が含まれることがわかります。そこから、A１００ｇに１８ｇの食塩が含まれることも導けます。本問も落とせません。

(4)　答　９２．８㎝

弧の一部を移し替える扇形の平面図形の典型題。半径が等しいことを利用し、補助線を引いて正三角形を作る考え方は本校を受験する生徒としてはしっかり持っておきたいところ。直線である６㎝×５つ分も足し忘れることのないように。

［３］ここからは大問になります。約束記号を含んだ、場合の数の問題。

(1)　答　１５通り

百の位の数字＋十の位の数字＋一の位の数字＝５になる和分解を考えます。００５、０１４、０２３、１１３、１２２となります。一番大きい位に０が来てはいけないことに注意し（(2)も同様）、あとはそれぞれの個数を考えれば答えが求まります。

(2)　答　２２通り

奇数なので、一の位によって場合分けをします。
・１の場合→千の位の数字＋百の位の数字＋十の位の数字＝５　⇒　(1)より１５通り
・３の場合→千の位の数字＋百の位の数字＋十の位の数字＝３　⇒　００３、０１２、１１１の組み合わせがあり、個数を合計して６通り
・５の場合→千の位の数字＋百の位の数字＋十の位の数字＝１　⇒　００１のみの組み合わせがあり、１００だけなので１通り

［４］特殊算が絡む、速さの文章題。今年は本問を、合否を分けた一題として詳細後述していきます。

(1)　答　２５分

(2)　答　１２分

(3)　答　１．８㎞

［５］補助線を引きながら、面積比を考えていく三角形を題材とした平面図形の問題。

どのように、補助線を引いて比を活用していけば良いのか、迷ってしまった受験生もいたのではないでしょうか。

(1) 答　２：１

まず、△BHDと△AFHが等しく、□HDEFを共通部分として各々に足して考えると、△ADEと△BEFも等しいことになります。△ADEの高さを辺AE、△BEFの高さを辺EFとしてとらえると問題文の条件からAE：EF＝２：１ですので、底辺比は逆比となってDE：BE＝１：２です。
そのことから、BD＝DEとなり、このこととAF＝FEであること、高さの同じ三角形同士は面積比＝底辺比であることを利用し、点Eから点Hにむかって直線を引いて三角形をわけてみると以下のようになります。
2018_gouhi_sansu
よって、BH：HFは△BHEと△HEFの面積比から導き出せます。

(2) 答　３：５

(1)でわかったことを整理すると以下のようになります。
2018_gouhi_sansu2
三角形全体の面積は２０㎠なので、△AECは２０－（４＋２＋２＋２＋２）＝８㎠です。ここから、BD：DE：EC＝△ABD：△ADE：△AECであり、６：６：８＝３：３：４となります。さらに、点Cから点Fにむかって直線を引いて△CEFを考えます。BE：EC＝（３＋３）：４＝６：４＝３：２なので、△BEFと△CEFの面積比も３：２となり、△CEFは４㎠と求まります。あとはAG：GC＝△ABF：△FBCとなるので、計算すれば答えが求まります。

［６］最後の大問であり、昨今の入試で良くテーマとして扱われる立体図形および平面図形の問題。“交わる”という表現に戸惑った受験生も多くいると思われます。(1)～(3)を通じてかなりの難問と言えます。

(1) 答　２㎝

実際に問題文の情況を作図してみると、以下のようになります。
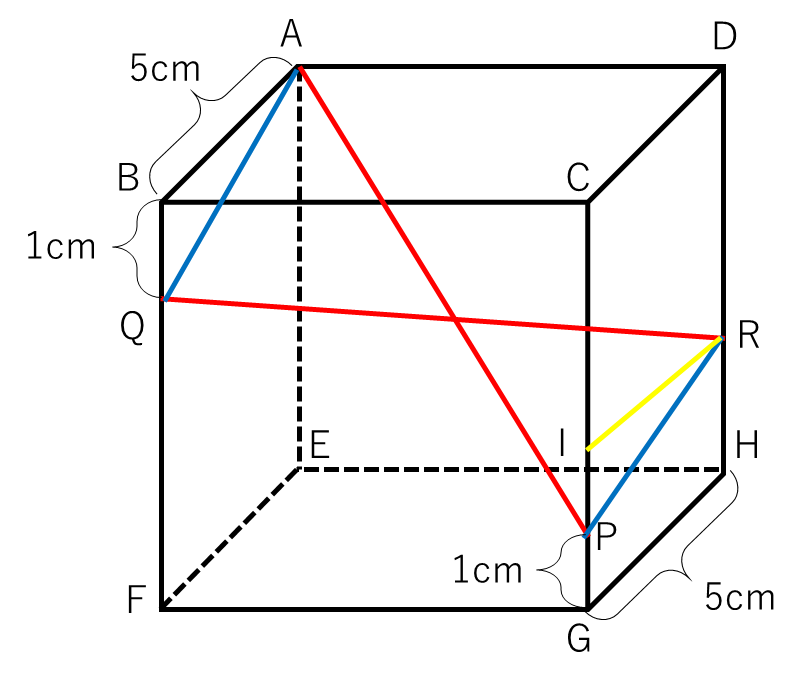
2018_gouhi_sansu3
AP、QRが交わるということは、上図の青線で示したAQとPRが平行になるということです。AQに着目してみると、上に１㎝上がり（BQ）、横に５㎝伸びています（AB）。同じ動きをPRで考えてみると、Pから上に１㎝上がり（IP）、横に５㎝伸びています（IR）。ここから、HRの長さが求まります。

(2)答　２５㎤

(1)と同じ情況であることがわかります（点Rは点Tと一緒、点Qは点Sと一緒）。
問題の四角すいU-EFGHは以下の黄色い立体です。
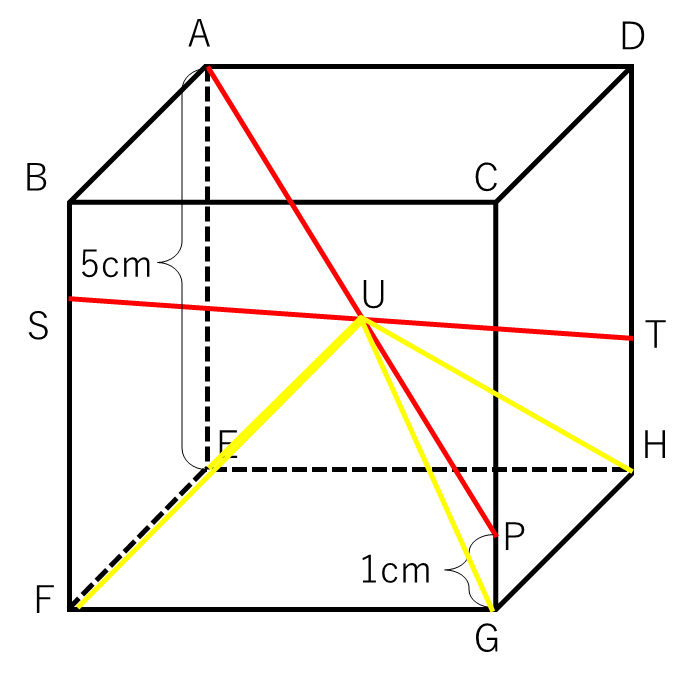
2018_gouhi_sansu4
底面積は正方形EFGHなので５×５＝２５㎠。高さは、辺AEと辺PGの平均を求めれば
良いので、（５＋１）÷２＝３㎝となります。ここから、体積が求まります。

(3) 答　㎤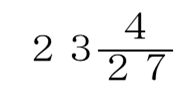

本入試、最後にして相似を使ったかなり高難易度の問題です。
まず、AからPに向かって引いた線を延長し、砂時計相似（図の△AVXと△WJX）を作ると以下のようになります。
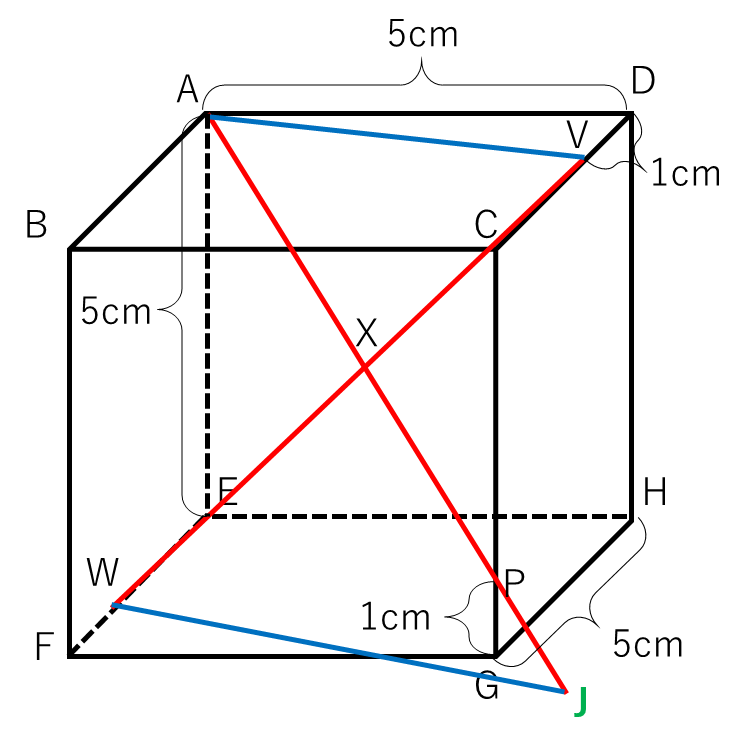
2018_gouhi_sansu5
その相似を利用し、VA：JWを求めれば、高さ比を利用して四角すいX-EFGHの高さが求まります。
△AEJと△PGJのピラミッド相似を利用すると、EG：GJ＝４：１となります。
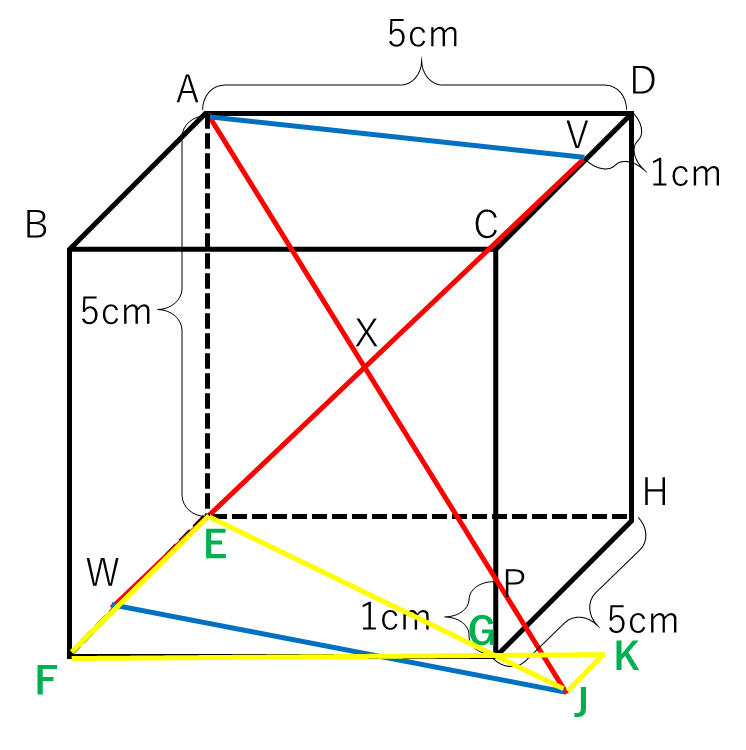
2018_gouhi_sansu6
続けて、△EFGと△GJKの砂時計相似を利用すると、FG：GK＝４：１となり、辺FKを計算すると６．２５㎝と求まります。
以上のことから、相似の考え方を活用し、VA：JWは各々の辺が対応する横の長さであるAD：FKと同じであり、５：６．２５＝４：５とわかります。このことから、問題となっている四角すいの高さが求まり、体積が導き出せるわけです。

合否を分けた一題

今回は、後半の大問群の中で速さの単元である大問４について合否をわけた一題として紹介しましょう。決して易しい典型題などではなく、様々な考え方を複合して考えていかなければならず、差がついた問題と言えそうです。

［４］速さ・鶴亀算

(1)

問題文後半の条件から、Aが家から公園までかかる時間とBが家から公園までかかる時間の合計は２２＋２３＝４５分となります。よって、Bが家から公園までかかる時間はAのそれを除くので、４５－２０＝２５分となります。

答え：２５分

(2)

家から公園までかかる時間は、A…２０分、B…２５分となるので、時間比はA：B＝４：５となり、速さ比はA：B＝５：４となります。ここでAの速さを５／分、Bの速さを４／分とおくと、家から公園までの距離は５×２０分（４×２５分）＝１００となります。家から図書館までAが５／分の速さでかかった時間と、図書館から公園までBが４／分の速さでかかった時間の合計が２２分であり、合計の距離が１００なので鶴亀算を使います。したがって、答えを求めると１２分となります。（もちろん、２３分の条件を使ってもかまいません。）
答え：１２分

(3)

３人目の人物であるCが登場し、３人旅人算を考えていく難問です。全員の動きを線分図にすると、以下のようになります。
2018_gouhi_sansu7
上図から、AとCが２０÷５(１６÷４)＝４分後に出会ったことがわかります。また、CはAと出会うまでに３６０×４＝１４４０ｍ進んだことになり、Aは家から公園まで２０分かかるので、この距離を２０－４＝１６分かかって進んだことになります。ここから、Aは１４４０÷１６＝９０ｍ／分となり、家から公園までの距離は（３６０＋９０）×４分＝１８００ｍ＝１．８㎞となります。
答え：１．８㎞