算数の合否を分けた一題
豊島岡女子中入試対策・算数の合否を分けた一題(2016年度)
難易度分類
| [1] | (1)A (2)A (3)A (4)B |
|---|---|
| [2] | (1)A (2)A (3)B (4)A |
| [3] | (1)A (2)B |
| [4] | (1)B (2)B |
| [5] | (1)A (2)B (3)B |
| [6] | (1)A (2)B (3)B |
A…豊島岡女子合格を目指すなら必ず得点したい問題
B…着眼点や解法ツールにより正答率・かかる時間に差がつく問題
C…難易度や処理量から判断して、部分点狙いで答案を作成すべき、もしくはとばすべき問題
出題総評
計算問題と一行問題が8問、大問4題の出題構成は例年通りです。難しいレベルの出題はほとんどありませんが、平面図形・立体図形でやや難しい問題が出題されています。昨年はサンデーショックの影響で得点率が下がりましたが、今年は例年並まで上がるものと思われます。
問題別寸評
計算と一行問題から成る小問集合でした。
(1)
小数と分数の混じった四則計算です。確実に正解したいです。
(2)
分数の計算問題です。そのままでも解けますが、計算の工夫を用いれば短時間で解答することもできます。
(3)
仕事算の問題です。基本レベルの問題ですので確実に正解したいところです。
(4)
数の性質の問題です。小数第1位で割り切れる、という条件から3÷□の答えも0.1から0.9まで絞られますので、一つずつ調べていってもよいでしょう。もちろん、□が30の約数のうち3の約数でない数である、という条件を導いても良いです。
[1]に続いて一行問題4問から成る小問集合です。速さ・食塩水・調べ上げ・角度の4問が出題されました。
(1)
速さの問題(旅人算・つるかめ算の融合)です。2人の出発地点と進行方向を確認し、確実に正解したい問題です。
(2)
3つの食塩水を混ぜ合わせる問題です。それぞれの混ぜ合わせは難しくありませんので、こちらも確実に正解したい問題です。
(3)
数字の組合わせを調べる問題です。合計が等しいところから数字の差に注目していくことがポイントです。答えが複数ありますのでしっかり調べて回答できたかがポイントです。
(4)
平面図形の角度の問題です。2つの部分の角度を比で表し、式を立てられたかどうかがポイントです。
規則性・数の性質の問題です。(1)で求めた結果から規則を見つけ、その規則を用いて(2)を解く、という設問の流れをおさえられたかがポイントです。
(1)
いろいろ解き方を考えるよりも、実際に計算して求めたほうが早かったようです。問題としては難しくありませんが、この結果から「2を並べた個数から2個減らした数だけ3が並ぶ」という規則を見つけられたか、が(2)につながります。
(2)
(1)の結果から、かけ算の答えが、27333……33306、となることがわかります。
ここに並んでいる各位の数の和が100の倍数になることから、3が何個並んでいるかを求めていきます。規則性の問題は、規則性をしっかり把握してから解くようにしていきましょう。
平面図形の折り返しと面積に関する問題です。直角三角形の相似を見つけられたかが大きなポイントです。
(1)
折り返しの問題では、同じ角度がいくつも出てきます。それらに記号を付けていき、相似形を見つけるといいた解法が問われる問題です。
(2)
今度は平行直線が出てきます。そこから分かる等しい角度にやはり記号をつけていくことで、新たな相似形が見つけられたかがポイントです。相似である全ての直角三角形は、三辺の長さが3:4:5の関係になっていますので、相似形が見つかればその後の計算は難しくはなかったと思われます。
峠を使った旅人算と比の問題です。最初に2人の動く様子をしっかり図にし、速さの比を道のりの比に置き換えて図に数値を書き込んでいけたかがポイントです。
(1)
2つの区間の道のりの比を求める問題です。2人がC地点ですれ違ってから、B町と山頂に到着するまでの時間が等しいことがわかれば、速さの比と道のりの比が等しいことにはすぐ気が付けたのではないでしょうか。
(2)
問題文の中では触れられていない、「豊子さんが山頂についた時」の図を考えるのがポイントです。(1)で求めた道のりの比を用いて、各区間の道のりも比で表わしていくことがポイントです。
(3)
2回目に出会った地点を求める問題です。ただし、ここまでの誘導が丁寧に作られていますので、(2)①が解けた受験生であれば、最後まで完答することができたものと思われます。
影の面積についての問題です。光源が移動する問題は、女子校の出題としては珍しく、難しい問題でした。ただし、自分で作図をして考えるための図も与えられており、(2)①できちんと作図が出来ていれば、その後の②も解きやすかったものと思われます。
(1)
点光源が地面にうつす影の長さを求める問題です。しっかりと横から見た図を描き、相似形を見つけられれば正解できたのではないでしょうか。
(2)
①点光源が地面にうつす影の面積を求める問題です。類題を解いたときにきちんと作図も練習できていたかがポイントです。
②点光源が動いたときに影にならなかった部分の面積を求める問題です。点光源Pが移動する辺の両端にあるときの影の図を描くことで、影にならなかった部分の面積を求めることができます。
合否を分けた一題
昨年はサンデーショックのため、2月2日に豊島岡女子ではなく女子学院を受験した受験生も多く、全体の平均点が下がる傾向にありました。今年は例年通り、1日に桜蔭または女子学院→2日豊島岡女子、と受験した生徒も多かったため、基本レベルを確実に正解し、やや難しい図形問題を取れたかが合否の分かれ目になったものと思われます。図形の折り返し、直角三角形の相似、影の作図など、幅広い知識や解法を習得し、しっかり使いこなせるまで演習しておかないと、今後も高得点勝負になりやすい豊島岡女子の算数に対応できません。注意しておきたいところです。
では、2016年度の合否を分けた一題として、[6](2)を取り上げたいと思います。
(2)
相似と影の問題
① Pから出た光が、地面に垂直に立てた棒に当たって作る影の関係を図にします。
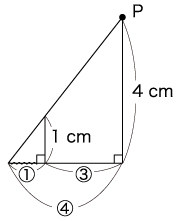
ここで底面において、光源から棒までの距離と影の長さの比は、常に3:1になることがわかります。そこで、点Pが頂点Aから1cmの位置にあるとき、底面にできる影は次のようになります。
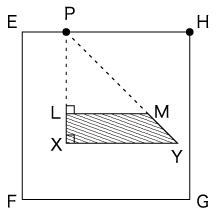
LM=2cm、XY=2×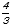 =2
=2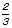 cm、LX=
cm、LX=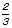 ㎝ になりますので、
㎝ になりますので、
影の面積は、(2+2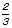 )×
)×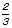 ÷2=1
÷2=1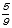 ㎠になります。
㎠になります。
② 点Pが頂点Aにあるときの影と、頂点Dにある時の影の2つを図にします。
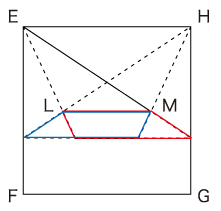
点Pが頂点Aから頂点Dまで移動するときに、少なくとも一度は影出会った部分は2つの影が重なる次の図の部分になります。
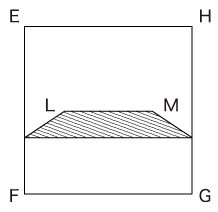
この面積は底面からひいて求めます。
影の面積は、(2+4)×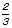 ÷2=2㎠となりますので、答えは
÷2=2㎠となりますので、答えは
4×4-2=14㎠です。
豊島岡女子中入試対策・関連記事一覧
豊島岡女子中入試対策・同じ教科(算数)の記事
豊島岡女子中入試対策・同じテーマ(合否を分けた一題)の記事
- 理科の合否を分けた一題(2012年度)
- 算数の合否を分けた一題(2015年度)
- 国語の合否を分けた一題(2015年度)
- 国語の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2016年度)
- 理科の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2017年度)
- 国語の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2017年度)
- 社会の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2018年度)
- 理科の合否を分けた一題(2018年度)
- 国語の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2019年度)
- 理科の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2020年度)
- 社会の合否を分けた一題(2020年度)
- 国語の合否を分けた一題(2020年度)
- 理科の合否を分けた一題(2020年度)
- 算数の合否を分けた一題(2021年度)
- 国語の合否を分けた一題(2021年度)
- 社会の合否を分けた一題(2021年度)
- 理科の合否を分けた一題(2021年度)