算数の合否を分けた一題（2015年度）

算数の合否を分けた一題

豊島岡女子中入試対策・算数の合否を分けた一題（2015年度）

難易度分類

［１］	（１）Ａ　（２）Ａ　（３）Ａ　（４）Ｂ
［２］	（１）Ａ　（２）Ａ～Ｂ　（３）Ａ　（４）Ｂ
［３］	（１）Ａ　（２）Ａ
［４］	（１）Ｂ　（２）Ａ　（３）Ａ
［５］	（１）Ａ　（２）Ｃ　（３）Ｂ
［６］	（１）Ａ　（２）Ｃ

Ａ：豊島岡女子合格を目指すなら必ず得点したい問題
Ｂ：着眼点や解法ツールにより正答率・かかる時間に差がつく問題
Ｃ：難易度や処理量から判断して５分以内に解き切る腕力がなければ一旦とばすべき問題

問題別寸評

冒頭の［１］は小問集合

（１）は何の変哲もない順算の計算問題。

（２）速さと比の問題。
距離の比２：１、時間の比５：１から、速さの比を求めればよいだけです。

（３）数の性質の問題。
ある数でわると余りが等しくなるという、上位生にとっての典型題です。差の公約数を求めましょう。

（４）数の性質の問題。
単位分数の和で表すという、こちらも典型題です。できるだけ大きい単位分数を引いていくという手法により、単位分数の和で表すことができます。
ただし、今回は分母がすべて１けたの整数という条件に注意が必要です。をひいたあと、できるだけ大きい単位分数をひくと残りがになってしまうので、、と順番に試してみると、をひいたとき残りがとなります。

［２］も小問集合

（１）つるかめ算。
面積図を利用し、りんごの代金４００円分を除き、面積が等しい２つの長方形において逆比で処理してもよし。
もしくは、全部りんごを買ったときの代金差４２００円から代金差４００円まで、３８００円を縮めるにはみかんを何個買えばよいのかと考えてもよし。

（２）割合と比の文章題。
２つの式を立て、消去算に持ち込むのが一般的です。今回は数値がいずれも５％と８％なので、和差算に持ち込むことも可能です。いずれにしても、文字や丸数字を含んだ式を操作する力が求められます。昨年の合否を分けた一題として取り上げた２０１４年度第１回［５］も、文字や丸数字を含んだ式を操作する力がないと解き切れない問題でした。豊島岡女子を目指す受験生にとって必須の力といえます。

（３）約束記号の問題。
【２１】～【３０】は０になることを考えると、工夫の余地を考えるより、地道に計算した方が速いでしょう。

（４）平面図形と比の問題。
まずは△PAEと△PBGのピラミッド相似に気づくかどうか。
その後、正方形PQRSの１辺の長さを求めようとはせずに、４つの合同な直角三角形と正方形ABCDの面積をたすという方針を立てられたかです。

前半戦［１］［２］の小問集合に続いて、［３］からは大問が続きます。

［３］数列の問題

１・２・３だけを使うことから、「ホテルの部屋番号で４と９を除く問題」のようにN進法の問題だと早とちりした受験生がいたようです。N進法の位取りと少し似ていますが、別物です。

（１）１けたの数、２けたの数、３けたの数と場合分けして数え上げるとすっきりします。全部で３９個しかないので、書き出して確認した受験生が多かったことでしょう。

（２）これも設問（１）と同様に、１けたの数、２けたの数、３けたの数と場合分けして和を求めましょう。２けたの数の和１１＋１２＋１３＋２１＋２２＋２３＋３１＋３２＋３３＝１９８は、３けたの数の和を求めるときに利用できます。たとえば百の位が１の３けたの数の和は、百の位だけ別にして
１１１＋１１２＋１１３＋１２１＋１２２＋１２３＋１３１＋１３２＋１３３＝１００×９＋１９８
と計算するのがラクでしょう。

［４］流水算のダイヤグラムの問題

途中でエンジンが止まって流される問題は流水算の典型題です。ただ、今回はダイヤグラムでの出題なので、必要な情報をダイヤグラムから読み取れたかどうかでしょう。
また、設問（１）を落とすと連鎖的に３つの設問とも失点するという、速さの大問特有の怖さがあります。しかも３つの設問のうち、（１）が最もつまずきやすいという、受験生泣かせの大問です。

（１）比を利用して計算できたかがポイントです。
R地点から流されて再びR地点までもどるのにかかった時間が８７.５－１５０００÷４００＝５０分なので、４０分流されて１０分でもどったことがわかります。ここから、距離一定、時間４：１なので、川の流れの速さと上りの速さの比が１：４と求められます。

（２）AとBの静水時の速さが同じという、問題文冒頭の条件を見落とさなければ大丈夫でしょう。

（３）下りの速さと川の流れの速さで１５ｋｍ進むのに５０分かかったことから、つるかめ算であることを見抜きましょう。といっても、途中でエンジンが止まって流される問題を解いた経験がある受験生は、つるかめ算が念頭にあったはずです。

［５］正三角形のマス目を利用した正六角形の問題

正多角形を好んで出題する豊島岡女子対策として、男子校の過去問（正三角形のマス目の図形問題は麻布が定番）で訓練してきた受験生にとっては力を発揮できた問題ですが、図形を苦手とする受験生にとっては厳しい問題です。ただ、設問ごとの関連性がなく、それぞれが独立した問題なので、（２）だけ、（３）だけ得点することが可能です。

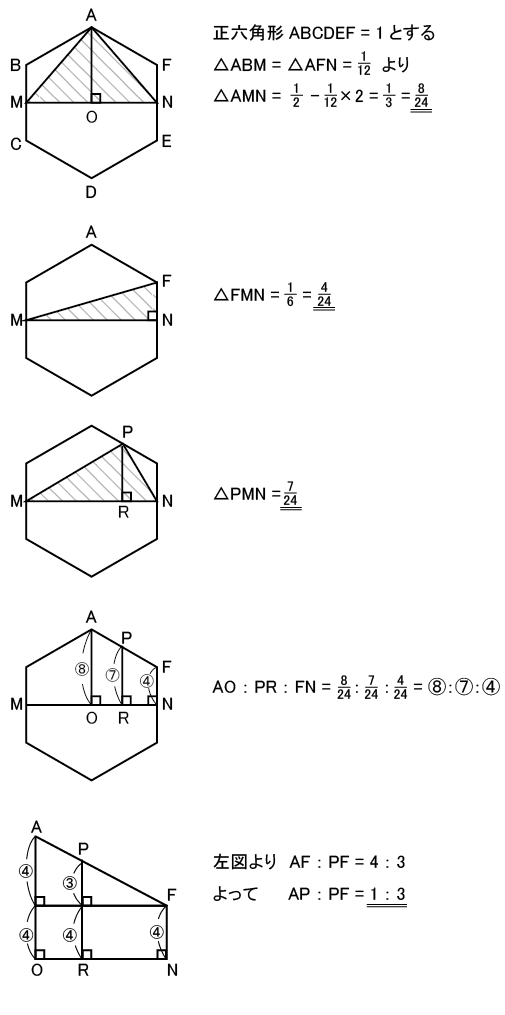
（１）様々なアプローチの仕方が考えられます。１つの考え方に固執せず、複数の解法を探ってみてください。ここでは解法例として１つ挙げておきます。
△PFNは正六角形ABCDEFの
△PMNを分割すると、△PFN６個分なので、＝

（２）後ほど詳述します。

（３）同様の問題を解いた経験があるかないかで正答率に差がついたことでしょう。Nから真上に直線を引き、初めて斜めの点線と交わった点をQとします。このときPN＝PQとなるので、MQとAFの交点がPであるときMP＋PQが最小、つまりMP＋PNが最小になります。

［６］立体図形の問題

立方体を積み重ねてできた直方体において、対角線との交点が何か所あるかを求める問題です。
平面図形において、１辺１ｃｍの正方形をしきつめてできた長方形に対角線をひいたときに、交点が何か所あるかという問題は典型題なので、どの受験生も解いたことがあるはず。それを生かせたかどうかです。

（１）は真上から見た図、正面から見た図を利用し、交点をとらえましょう。立体図形の問題を解く際に、立体を平面化してとらえるのは定石です。

（２）は設問（１）を利用して考えます。２０ｃｍ・３０ｃｍ・６０ｃｍという３辺の長さから、対角線上に設問（１）の直方体がちょうど１０個あることがわかります。１つの直方体につき交わりは４か所ずつ、でも最後の直方体はBにあたる点を除く必要があることを忘れずに。

合否を分けた一題

今年度の第１回入試の算数は、受験者平均点５１.２７、合格者平均点６４.８７。
第２回入試（受験者平均点６４.０９、合格者平均点８２.８３）、第３回入試（受験者平均点５５.８８、合格者平均点７７.７６）と比べても、また例年と比べても、平均点が低いといえます。

その大きな要因として挙げられるのが、サンデーショック。
例年であれば２/２に豊島岡女子を受験して平均点を一気に引き上げるはずの最上位層が、今年度は女子学院を受験して不在だったため、平均点が上がらなかったといえます。２/１桜蔭・２/２女子学院・２/３豊島岡女子と３戦３勝の受験生が多数いたことから、２/３第２回入試の平均点が高いのもうなずけます。

出題形式・問題数・配点は例年通りです。頻出の「作業を伴う条件整理」、「点の移動」は出題されませんでした。
総じて上位生にとっての典型題からの出題が多く、幅広い知識・解法を習得し、それらを使える状態にまで仕上げていないと得点できないセットです。特に［５］正三角形のマス目を利用した正六角形の問題では、３つの設問が関連せずに独立しており、平面図形の幅広い知識・解法を持ち合わせている受験生ほど有利でした。

では、２０１５年度の合否を分けた一題として、その［５］（２）を取り上げます。

［５］（２）