算数の合否を分けた一題
東海入試対策・算数の合否を分けた一題(2020年度)
難易度分類
| 大問1 | (1)A (2)A、A (3)A |
|---|---|
| 大問2 | A |
| 大問3 | (求め方)B (答え)B、B |
| 大問4 | (1)C (2)C |
| 大問5 | (1)A (2)C (3)C |
| 大問6 | (1)B (2)B |
| 大問7 | (1)A (2)A (3)B |
A・・・東海中合格を目指すなら、確実に正解したい問題
B・・・知識、解法次第で、得点に大きく差がつく問題 ⇒ 合否を分けた問題
C・・・難易度、処理量から判断して、正解できなくても合否に影響しない問題
問題別寸評
(1)四則演算
一般的な四則演算です。確実に正解しましょう。
(2)場合の数、数の性質
場合の数の方は、0が先頭にきても良いという条件さえ見落とさなければ平易な問題です。確実に正解しましょう。
答えは22、202、220、2002、2020、2200の6個となります。
次に、これらから2つの数を選び、積が444400になるもの2種類を答える問題です。
まず、22は残りの5つのうち、どれをかけても6けたにならないので、除外できます。
この数字の中で2つの数をかけて6けたになる組み合わせは、3けたの202か220を4けたの2002か2020か2200にかけたときです。
すると、202×2200と220×2020の積が444400になると分かります。
この問題も難しくはないので確実に正解しましょう。
(3)平均に関する問題
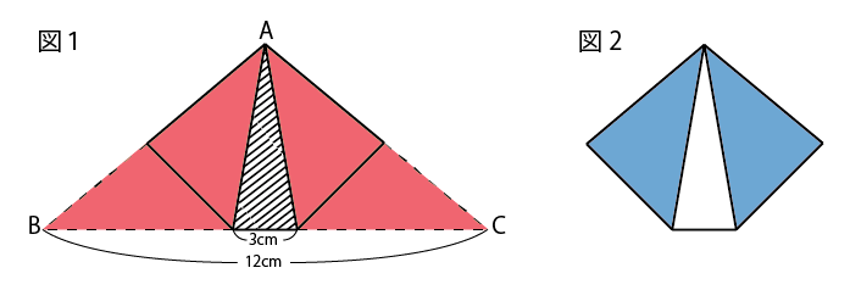
よくある平均に関する問題です。合格者は全体の40%なので、不合格者は全体の60%です。つまり、合格者の人数:不合格者の人数=2:3となります。
面積図で表すと、下の図のようになり、赤い部分と青い部分は面積が同じなので、赤い部分と青い部分の高さの比は③:②となります。⑤=16点なので、③は9.6点と分かります。
よって、合格者の平均点は54.6+9.6=64.2より、64.2点と分かります。

この問題は、電車の車両の数が多くなると進む速度も遅くなるという、あまり見かけない設定の問題でした。ただ、進んだ距離の差さえ出すことができていれば、すんなりと解けたのではないでしょうか。
情報量が少し多いので、まず情報整理をします。
・1両(=48m)だと、トンネルに入り始めてから完全に出るまでに56秒かかる・・・①
・3両(=144m)だと、トンネルに入り始めてから完全に出るまでに69秒かかる・・・②
・3両だと、1両で走るときよりも1秒あたりに進む距離が2m短くなる。・・・③
①、②より、3両だと1両のときより、96m多く走らなければトンネルを通過できないことが分かります。
②、③より、3両だと1両のときより、69秒で138m進む距離が短くなると分かります。
よって、トンネルを通過するのに3両だと1両のときより(96+138=)234m多く進まなければいけないことが分かります。
つまり、234mの差が(69-56=)13秒でできるということは、234÷13=18より、1両のときの速さは秒速18mと分かります。
トンネルの長さは56×18-48=960より、960mと分かります。
(1)
合同な図形やクロス型相似から辺の長さを求め、クロス型相似から比合わせをし、最後は「Aをねらえ」という根本原理を用いて求めます。
解答にたどり着くまでの手順も多いですし、何度も複雑な計算をする必要があるので、正しい解答にたどり着けた受験生は少なかったかもしれません。
では、まずは相似比を求めるのに必要な情報を手に入れるために図に書き込まれている以外の辺の長さを求めます。すると、三角形ADEと三角形CEBはこの図を角出しすると、合同であることが分かります。

次にクロス型相似から辺の長さを出していきます。


次に三角形EGHの大きさを求めるのに必要な辺の比を求めていきます。
HG:GF、HE:EIの比が分かれば三角形EGHが三角形HFIの何分の何かが分かるのでそれらを求めるのに必要な辺の比を求めていきます。
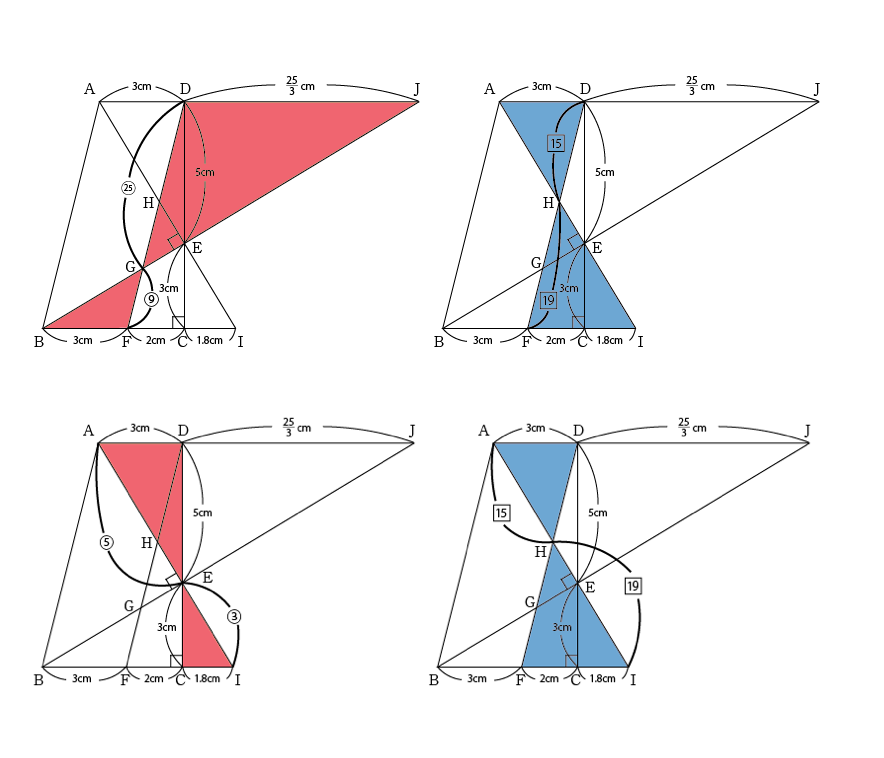
上図より、比合わせをするとHG:GF、HE:EIが分かります。下の図にまとめます。
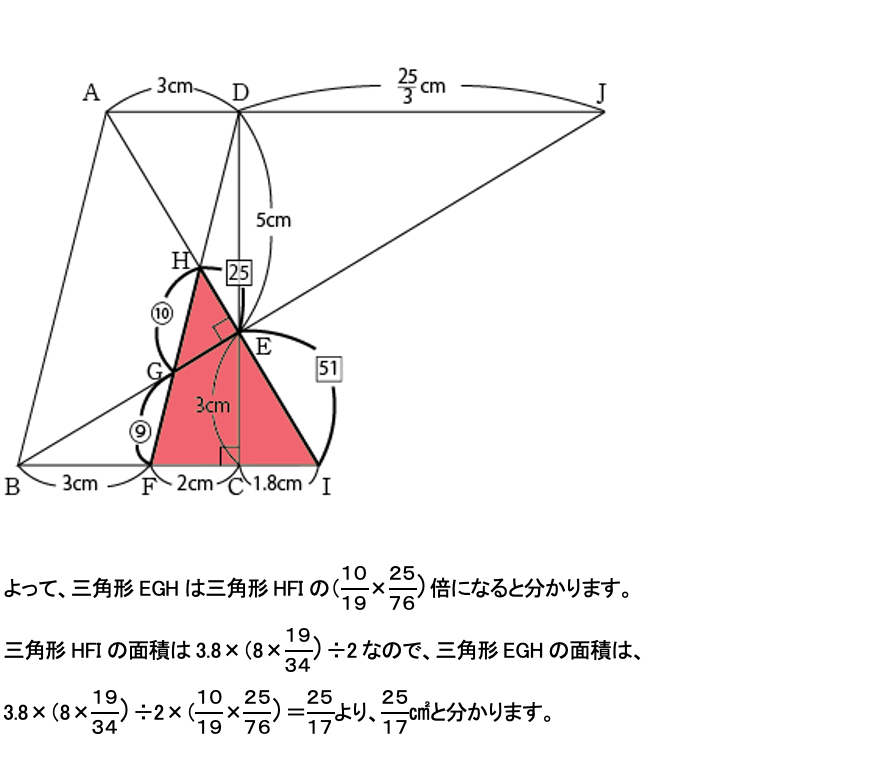
(2)も(1)で求めた情報を用いて同様に考えれば正解が導き出せます。
(1)

(2)(3)

(1)

(2)
太郎君と次郎君が2度目に同時にP地点に着いたのは太郎君が7周、次郎君が5周したときとあるので、最初に同時にP地点に着いてから太郎君も次郎君も2周したと分かります。どちらも2周で同じ時間になる組み合わせは太郎君がBコースとCコースを1周ずつし、次郎君がAコースとBコースを1周ずつしたときのみです。そのとき、両者ともに5分なので、9+5=14より、2人が走り始めてから14分たったときと分かります。この問題も大問5の(1)同様、2枚目の問題が難しい東海の中では簡単な問題なので、確実に正解したいところです。
(3)

合否を分けた一題
この問題は解法さえ知っていれば、3分以内には解けてしまいます。逆に知らなければ10分、20分では解けなかったでしょう。そのため、解法を知っているか知らないかで大きく差がついた問題となります。よって合否を分けた一題とさせていただきました。
(1)
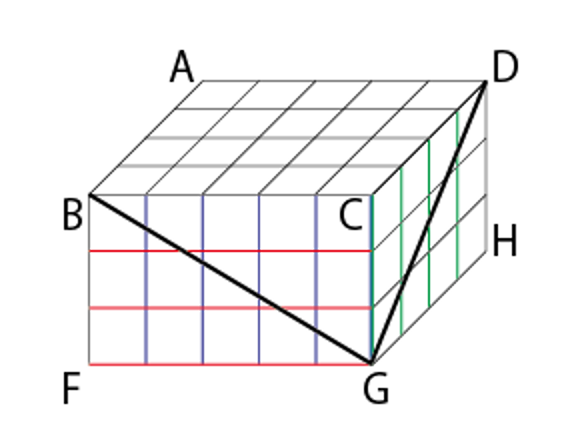
対角線AGが通る立体の個数を求める問題です。このような立体図形の通過の問題は2平面で相互的に考えることが多いですが、この問題の場合、通過する立体の数が多いので、かなり正確に図を書かなければいけません。そのため、解法は合っていたが、正解には至らず、という受験生も多かったのではないでしょうか。では、一瞬でかつ正確に解く方法を説明します。
2平面で捉えるところまでは同じです。あとは直線を引き、目で見て線の数を数えるだけです。
まずは、正面から見たBCGF平面で考えます。すると、BからGに直線が引けます。このとき、BからGにたどり着くまでに縦と横に何本の線を通るかを数えます。すると、縦に3本、横に5本通ると分かります。そして、縦線と横線が交差しているところをBGが通っていないかを確認します。BGは縦に3本と横に5本進むので、最後のG以外縦線と横線が交差しているところは通りません。
次に、真横から見たCDHG平面で考えます。すると、DからGに直線が引けます。このとき、DからGにたどり着くまでに縦と横に何本の線を通るかを数えます。すると、縦に4本、横に3本通ると分かります。そして、縦線と横線が交差しているところをBGが通っていないかを確認します。BGは縦に3本と横に4本進むので、最後のG以外縦線と横線が交差しているところは通りません。
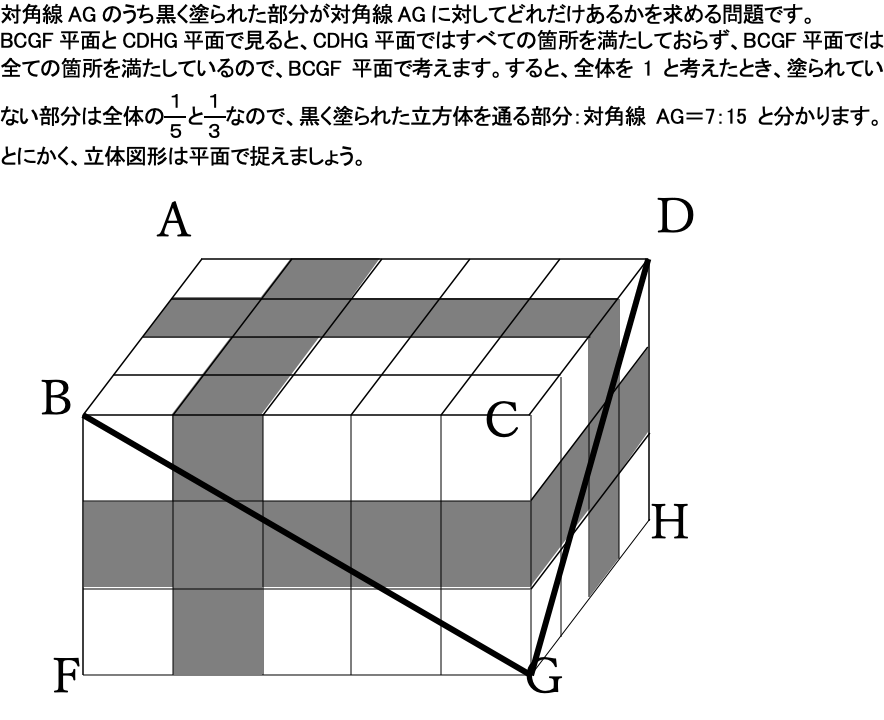
よって、下の図のように3辺で考えると、(3+5+4−1−1=)10個の立体を通ると分かります。
この方法を知っていれば、赤、青、緑の本数と、2平面それぞれで黒い直線と縦横の交差しているところと交わっていないかを確認するだけです。2平面を相互的に書いた図で解くより圧倒的に早く解けるので、知らなかった方は是非覚えてください。
(2)
総評
今年度の入試は大問数、小問数ともに例年通りの範疇でしょう。
算数は点数の面で見ると、ほぼ例年通りですが、受験者平均と合格者平均の差がこの10年で2番目に大きかったです。大問3、6、7の出来に大きな差があったと考えられます。
出題構成としては、大問7つのうち、4つが図形問題、2つが速さの問題でした。残りの1つは計算問題を含む3問の小問集合です。例年、図形問題と速さが出題のウェイトの多くを占めますが、今年はさらに顕著だったのではないでしょうか。時折、数の性質や規則性なども見かけるので全体的に対策は必要ですが、東海中学の合格を勝ち取るには言うまでもなく図形問題と速さの完成度を上げることが大切です。