国語の合否を分けた一題
東海入試対策・算数の合否を分けた一題（2016年度）
難易度分類
| １ | （１）Ａ （２）Ａ |
|---|---|
| ２ | （１）Ａ （２）Ｂ |
| ３ | （１）Ｂ （２）Ｂ |
| ４ | Ｂ |
| ５ | （１）Ａ （２）Ｂ |
| ６ | （１）Ｂ （２）Ｂ～Ｃ |
| ７ | （１）Ｂ （２）Ｂ （３）Ｂ |
| ８ | Ｂ～Ｃ |
A…東海中合格を目指すなら必ず得点したい問題
B…着眼点や解法により正答率・かかる時間に差がつく問題
C…難易度や処理量から判断して、後回しにしてもよい問題
問題別寸評
（１）
小数・分数混合の計算問題です。ここは落ち着いて確実に正解しなくてはなりません。
（２）
和のほうはいくつかの解法が考えられますが、個数が２×２×２＝８個しかありませんから、仮に全て書き出したとしてもたいした計算量ではありません。しっかり正解しておきたい問題です。
（１）
図に表れている三角形は、全て正三角形ですね。ＤＥ＝ＥＦ＝ＥＣとなりますから、ＡＢ：ＤＥ＝7：4より、ＢＥ：ＥＣ＝3：4です。あとは相似比と面積比の関係を用いて答えが得られるでしょう。
（２）
折り返しの問題は本校でも頻出です。通常は、折り返す前の図形が図に点線で描かれていることが多いのですが、本問のように描かれていない場合には、まずは自分で元の図形を補っておくことが大切な作業です。
図２に、折り返す前の三角形ＧＨＩを点線で補ってみましょう。すると図２の角Ｐが６０度であることが容易に分かります。さらに、図２において、角Ｐ＋角Ｉ＋角Ｈ＝角㋐であることを用いて考えてみると良いでしょう。
立体の入った水そうに水を注ぐという設定の、本質的には頻出問題に過ぎないのですが、与えられた図がやや目新しく、とまどった受験生もいたでしょう。
（１）
㋐、㋑、㋒の底面積は、それぞれ50㎠：200㎠：78.5㎠＝100：400：157です。高さの比は1：3：4と表せますから、体積の比は(100×1)：(400×3)：(157×4)＝25：300：157と求められます。
この合計が2410㎤であることから答えを求めましょう。
（２）
水そうの底面積のうち、㋐㋑㋒の底面積を除いた部分を㋓とします。
グラフと（１）の結果から、㋓に2.5cmの水が入るのに5分、㋓＋㋐に5cmの水が入るのに12分かかったことが分かります。このことから、㋓：㋐を求めることによって、答えを出しましょう。
一見、よくありそうな売買算ですが、受験生にとってはやや解きにくかったかもしれません。
仕入れ値を⑩とすると、定価は⑳、割引後の売値は⑭と表すことが出来ますね。
仮にすべてが定価で売れたとすると利益は36000円、実際の利益は22500円です。
定価で売った時の利益は1個当たり⑩、割引後の1個当たりの利益は④となりますから、つるかめ算の考え方を用いて解くのがスマートです。
この発想に至らなかったとしても、仕入れた個数を1とし、定価で売れたのが30個ですから、割引後に売ったのは1－30個と表して、
⑩×1＝36000円
⑩×30個＋④×(1－30個)＝22500円
という2つの式から強引に求めていくことも可能です。
（１）
まずはルール通り、周期がはっきりするまで書き出していきましょう。
7,2,4,8,2,6,2,2,4,8…
となって、1番目の「7」を除いて2番目からの「2,4,8,2,6,2」が繰り返していることが分かります。
1番目を除いて考えるので、個数の処理ミスに注意が必要ではあるものの、東海中の出題としては基本的な周期算と言えます。
（２）
やはり初めは（１)と同様に、100番目が2になるのはどういう場合か調べます。2番目の数をいくつにすべきかを考えていくことになりますが、2番目の数が奇数であると、並ぶ数はすべて奇数になってしまうので、問題の条件に合いません。
（１）の場合に加え、2番目の数が「4」「6」「8」の場合を調べれば充分です(「0」にした場合は、3番目以降もすべて「0」になってしまいます)。
（１）
Ｋ寺では30秒ごと、Ｔ寺では40秒ごとに鐘をつきますから、同時につくのは最小公倍数の120秒ごとになります。Ｋ寺とＴ寺ではそれぞれ108回ずつ、計216回の鐘がつかれますので、120秒ごとに同時につかれた鐘の回数を求め、216から引いて求めるのが良いでしょう。
その際に注意すべき点が2つ。
①開始時刻である午後11時30分にも同時につかれていること
②Ｋ寺で108回目の鐘がつかれる30×107＝3210秒以降は、Ｔ寺のみで鐘をついているので、同時につかれることはないこと。
このあたりでのミスも生じそうなところで、試験場ではそれなりに手ごわい問題だったはずです。
（２）
午後11時30分の1回を除くと、以後120秒を周期として6回の鐘が聞こえることを確認してください(30,40,60,80,90,120秒)。すると、88回目の鐘の音が聞こえるのは、周期算の考え方から、
87÷6＝14あまり3
120秒×14＋60秒＝29分後
であることが求められます。
鐘をついた時刻については、解法次第で解答時間に差が出そうです。
「Ｔ寺では、30秒ごとに1人訪れて、40秒ごとに1人が鐘をついて…」とニュートン算のように考えたくなる受験生もいたでしょう。しかし、もっとシンプルに考えることができます。
88回目の鐘を聞いた後、Ａ君がＴ寺に到着するまでにかかる時間は、400÷60＝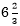
分→6分40秒ですから、（１）の結果と併せると、Ａ君がＴ寺に到着した時刻は午前0時5分40秒であることが分かります。
Ｔ寺には午後11時20分に1人目が訪れた後、30秒ごとに1人ずつ訪れていたのですから、
午前0時5分40秒－午後11時20分＝45分40秒
45分40秒÷30秒＝91あまり10秒
より、Ａ君が到着するよりも前に91＋1＝92人が訪れていました。すなわちＡ君はＴ寺で93人目に鐘をついたことになりますね。
あとは、「Ｔ寺では午後11時30分に1人目がついた後、40秒ごとに1人ずつ鐘をつく」ということから、Ａ君が鐘をついた時刻が計算できます。
７
うまく整理することができれば、少なくとも（１）（２）は難しくなく、（３）も正解するのに無理のない設問でしたが、条件の整理の仕方に戸惑った受験生も多いでしょう。詳しくは、「合否を分けた一題」として後述します。
８
平面図形が得意な生徒の演習問題としては興味深い設問ですが、試験場で正解までたどり着くのは、多くの受験生にとって難しかったであろうと思われます。解法がひらめけばラッキー、そうでなければ試験中に深入りすべきではない問題でした。
「与えられた図を、大きく長方形で囲む」というのが、おそらく受験生にとって最も分かりやすい解法でしょう。
図形が得意であれば、「2つの正方形の間に挟まれた、上下の2つの三角形の面積は等しい」という事実に納得できるかどうか研究してみるとよいでしょう。
合否を分けた一題
大問７～８題、小問１５題程度のうち１題で求め方の記述を要求するという形式は本年も踏襲されています。総合的な難易度も例年並みといってよいでしょう。
受験者平均点は５割前後で推移しています。標準的な合格者にとって、正解するのが困難なレベルの難問は多くありませんが、すんなりと不安なく解ける設問もせいぜい３～４題程度。2014年度から試験時間が60分に延長されていますが、すべての問題に本格的に手を付けていくというよりも、出来そうな問題を見極め、まずは６割あたりの得点を目標とする立ち回りが重要な試験です。
冒頭の難易度分類でＢやＣをつけたすべての問題が合否を分けかねない出題と言えますが、中から［７］を取り上げます。
７
（１）
まずは、「5人それぞれの合計得点は」「連続した5つの整数でした」という条件から、どのようなことが分かるでしょうか。
1回のゲームでの5人の得点の合計は、1～3回目までは1＋2＋3＋4＋5＝15点、4回目は2＋4＋6＋8＋10＝30点です。よって、4回のゲームでの5人の合計得点は、15×3＋30＝75点になります。
「連続した5つの整数」の合計が75点という事ですから、平均点は75÷5＝15点。すなわち、5人の得点は1位から順に、17点、16点、15点、14点、13点であったことが分かりました。Ａ君は合計得点で4位であったことから、合計得点は14点です。
（１）自体はこれで解決済みですが、この後のために、Ａ君について分かることをもう少し整理しておきましょう。
4回の順位が1位、2位、3位、5位でしたから、仮に4回目の得点が2倍にならないとすると、合計得点は、5＋4＋3＋1＝13点であったはずです。実際には14点だったのですから、2倍になったのは14－13＝1点のときだったことになります。
| 合計得点 | 名前 | 1～3回目の得点 | 4回目の得点 | |||
|---|---|---|---|---|---|---|
| 1位 | 17点 | |||||
| 2位 | 16点 | |||||
| 3位 | 15点 | |||||
| 4位 | 14点 | Ａ君 | 5点 | 4点 | 3点 | 1×2＝2点 |
| 5位 | 13点 | |||||
このように、分かったことを表にまとめながら解き進めていくのが定石です。
（２）
同じようにＥ君について考えます。
最後の条件から、Ｅ君の4回の順位は2位、3位、4位、5位でしたから、仮に4回目の得点が2倍にならないとすると、合計得点は、4＋3＋2＋1＝10点であったはずです。
さて、2倍になったのは何点のときだったのでしょうか。
合計得点は最低でも13点ですから、3点または4点が2倍になって、合計得点は13点または14点であったはずですね。しかし、（１）からＡ君の得点が14点であることが分かっていますので、Ｅ君の合計得点は13点しかあり得ません。
したがって、Ｅ君の4回目の順位は3位であったと分かりました。
| 合計得点 | 名前 | 1～3回目の得点 | 4回目の得点 | |||
|---|---|---|---|---|---|---|
| 1位 | 17点 | |||||
| 2位 | 16点 | |||||
| 3位 | 15点 | |||||
| 4位 | 14点 | Ａ君 | 5点 | 4点 | 3点 | 1×2＝2点 |
| 5位 | 13点 | Ｅ君 | 4点 | 2点 | 1点 | 3×2＝6点 |
（３）
Ｂ、Ｃ、Ｄ君についても、得点状況を整理してみましょう。
Ｃ君は、1位、3位、4位、5位だったので、2倍にならないとすると、5＋3＋2＋1＝11点。
Ｄ君は、1位、2位、4位、4位だったので、2倍にならないとすると、5＋4＋2＋2＝13点。
ここまで整理したことから、Ｃ君の2倍になった得点が求められます。
すでに4位と5位はＡ君とＥ君であることが分かっていますから、Ｃ君の合計得点は15点以上でなくてはなりませんね。そうすると5点が2倍になっていて、合計得点は11＋5＝16点であったことになります。
Ｄ君については、4点が2倍になって合計得点が13＋4＝17点であったか、2点が2倍になって合計得点が13＋2＝15点であったかの2通りの状況が考えられます。
ここからは、いくつかの方針が考えられますが、高々2通りの状況に絞れたので、両方の状況について調べてみるのが有力です。
①Ｄ君の4回目の得点が4点であったとき
| 合計得点 | 名前 | 1～3回目の得点 | 4回目の得点 | |||
|---|---|---|---|---|---|---|
| 1位 | 17点 | Ｄ君 | 5点 | 2点 | 2点 | 4×2＝8点 |
| 2位 | 16点 | Ｃ君 | 3点 | 2点 | 1点 | 5×2＝10点 |
| 3位 | 15点 | Ｂ君 | 計11点 | 2×2＝4点 | ||
| 4位 | 14点 | Ａ君 | 5点 | 4点 | 3点 | 1×2＝2点 |
| 5位 | 13点 | Ｅ君 | 4点 | 2点 | 1点 | 3×2＝6点 |
5人の4回目の得点に注目してみましょう。Ｂ君以外の4人が10点(1位)、8点(2位)、6点(3位)、2点(5位)と分かっているので、Ｂ君は残りの4点(4位)であったと分かります。
すると、Ｂ君の1～3回目の得点の合計は、15－4＝11点。4回目で4位になっているので、5点(1位)、4点(2位)、3点(3位)、1点(5位)のうちから異なる3つを選んだ和が11点になっているはずですが、そのような組み合わせはありません(実は、Ｂ君以外の1～3回目の得点に注目すると、表の網かけ部分のように2点が4回現れていることから、すぐに矛盾であることが分かります。余裕があれば考えてみましょう)。
②Ｄ君の4回目の得点が2点であったとき
| 合計得点 | 名前 | 1～3回目の得点 | 4回目の得点 | |||
|---|---|---|---|---|---|---|
| 1位 | 17点 | Ｂ君 | 計9点 | 4×2＝8点 | ||
| 2位 | 16点 | Ｃ君 | 3点 | 2点 | 1点 | 5×2＝10点 |
| 3位 | 15点 | Ｄ君 | 5点 | 4点 | 2点 | 2×2＝4点 |
| 4位 | 14点 | Ａ君 | 5点 | 4点 | 3点 | 1×2＝2点 |
| 5位 | 13点 | Ｅ君 | 4点 | 2点 | 1点 | 3×2＝6点 |
①と同じように考えると、Ｂ君の4回目の得点は8点(2位)、1～3回目の得点の合計は9点であることが分かります。
5点(1位)、3点(3位)、2点(4位)、1点(5位)のうちから異なる3つを選んだ和が9点になっているはずで、これは5＋3＋1＝9点という組み合わせが存在し、問題の条件にすべて合っています。
以上のことから、1位：Ｂ君 2位：Ｃ君 3位：Ｄ君と答えを求めることができました。
(1 投票, 平均値/最大値: 5.00 / 5)
Loading ...
東海入試対策・関連記事一覧
東海入試対策・同じ教科（国語）の記事
東海入試対策・同じテーマ（合否を分けた一題）の記事
他校の同じ教科（国語）の記事
