算数の合否を分けた一題（2020年度）

算数の合否を分けた一題

桐朋中入試対策・算数の合否を分けた一題（2020年度）

難易度分類

１	（１）Ａ　（２）Ａ　（３）Ａ
２	（１）Ａ　（２）Ａ　（３）Ａ
３	Ｂ
４	Ｂ
５	（１）Ａ　（２）Ａ　（３）Ｂ　（４）Ｂ
６	（１）Ａ　（２）Ｂ　（３）Ｃ
７	（１）Ａ　（２）Ｂ　（３）Ｃ

Ａ…桐朋中学校合格を目指すなら、確実に得点したい問題
Ｂ…知識、解法次第で、得点に大きく差がつく問題
Ｃ…難易度、処理量から判断して、部分点を拾えれば良しとする問題

出題総評

出題傾向に大きな変更はありませんでした。図や表による整理を要求する問題や、(1)や(2)を基にして後半の小問を考えさせる形式の誘導問題など、良問がそろっています。
典型問題の解法に習熟することは当然として、さらに一歩踏み込んだ算数学習を行っていることが必要となります。
桐朋中学を志望する受験生が過去問学習を行う際には、間違え直しを重視してください。なぜその問題を間違えてしまったのか。どのような視点を持っていれば、正しい解法に気づくことができたのか。そんなことを考えながら、過去問学習に取り組んでください。

2020年度　問題別寸評

大問１

計算問題です。
（１）（２）（３）数字の並びから、頑張れば工夫できる問題もありますが、そのまま計算してしまったほうが早いかもしれません。

大問２　小問集合

（１）割合の問題。線分図は描かず、計算のみで短時間で解きたいところです。
（２）仕事算の問題。仕事算やニュートン算は桐朋中学で頻出の単元のため、確実に抑えておきたいところです。
全体の仕事量を「8人×12日＝96」とおいて解く解法が一般的です。仕事算の問題には、全体の仕事量を最小公倍数で置く場合や、１と置く場合や、本問のように「人数×かかった時間」でおく場合もあります。
人が1種類なのか2種類（「大人と子供」など）なのか、人が1人なのか複数人なのか。問題の設定ごとに、どの解法の使うのか、明確に分けて認識しておくことが必要です。

（３）余白に、下のような簡単な図を描いて考えると良いでしょう。
桐朋中学を受験する生徒ならば、テキストの典型問題で学習済みだとは思いますが、それでも図を描くことでケアレスミスを減らすことができます。
素早く作図できるよう、普段から図を描くことでコツをつかんでおきましょう。
赤い円の部分は、3つの中心角を足すと360度になることを利用します。

大問３

売買損益・差集め算の問題です。

解き方は何種類かあります。そのうちの1つ、下のような図を描いて考える方法を紹介します。
個数がかかわる売買損益で、値段に変化がある場合、何が起きているのかを把握することが大変です。簡単な図を描くことで認識しやすくします。

一日目の売り上げは、〇×270です。
二日目の売り上げは（〇－18）×450＝〇×450－8100です。
二日目は一日目より5940円多いことから、これらの差を取ります。

「二日目」－「一日目」＝5940円
（〇×450－8100）－〇×270＝5940
〇×180＝14040
より、〇＝78円と分かります。

〇は一日目のお茶の値段であるため、この78円は一日目のお茶の値段です。
問題で問われていることは二日目のお茶の値段のため
78－18＝60　が答えとなります。

大問４

　
下図のように、与えられた条件を、丁寧に表で整理して考えることがコツです。問題文中の表は小さく、変化後の数値を書き入れるスペースがありません。自分でもう1つ表を書き、変化後の個数を目で見て分かりやすい形にまとめると良いでしょう。

すると、和と比がわかっていることから、求めることができます。
例えば、袋Aの、赤玉と青玉の比は90：105＝6：7　であり、また赤玉と青玉の個数の和は221－52＝169個と分かるので、それぞれの個数を求めることができます。
計算自体は難しくありませんが、短時間で表書き、条件を可視化できるかどうかが分かれ目となる問題でした。

大問５

　
約束記号やルールに関する問題は、桐朋中学の頻出です。もちろん過去問と同じ問題は出ませんが、作業手順や頭の使い方に深い共通点のある問題が毎年出題されています。
（１）や（２）の「やるだけ問題」を通じて、後半の問題を解くためのカギを見つける思考法のトレーニングを積むことが、合格への道です。その問題が何を求めているのか、どのような手順の施行を要求しているのか、出題者の気持ちを読みとる視点を持ちながら、過去問に取り組めると良いです。

（１）（２）

いわゆる「やるだけ問題」です。問題を通じて、設問分の意味を理解し、後半の（３）や（４）を考えるためのヒントを得ることが目的です。
この（１）と（２）の結果をもとに、規則や一般化された法則を探していくことになります。

（３）

2つの数を入れ替えたところ、30大きくなったとあります。（１）の問題で、3と4を入れ替えると10増えたところから、4と1を入れ替えると30大きくなることに気付けると良いでしょう。
闇雲に探すのではなく、「（１）か（２）のどちらかがヒントになっているのでは？」という思考法を持てると良いでしょう。

（４）

２つの数を入れ替えたところ182小さくなったとあります。
さて、（３）の問題では（１）がヒントとなっていました。ということは、この（４）は（２）がヒントとなっているのでは？　と予想を立てます。
（２）では、5と6を入れ替えると91大きくなりましたが、「それはなぜか？」と考えていきます。
角の数字と辺の数字を入れ替えた場合の数の変化を、ある程度一般化できれば（完全な一般化はできなくても大丈夫です）、正解の予想もつきやすくなります。

例えば、「182」の1の位が2であることから、「もし辺と角の数を入れ替えるなら、差が2の数を入れ替えれば良いのでは？」くらいの予想が立てられれば十分です。

（１）や（２）で行った作業を基にして、「どうしてそうなるのか？」といった発想・好奇心を大事にしながら、日々の学習を進めていくのが良いでしょう。

合否を分けた一題

大問６

点の移動と面積の変化の問題です。桐朋中学は速さと旅人算の問題が頻出ですが、本年は点の移動という形で出題されました。
典型的な解法パターンを知っていることはもとより、その注意点、利用できる範囲などを深く理解しているかどうかを問う良問でした。

（１）

まずは、丁寧に作図して考えましょう。大問５もそうでしたが、桐朋中学の（１）については、まずは作業するだけで答えが出る問題も多く出題されています（当然、後半の問題を解くためのヒント、誘導になっています）。

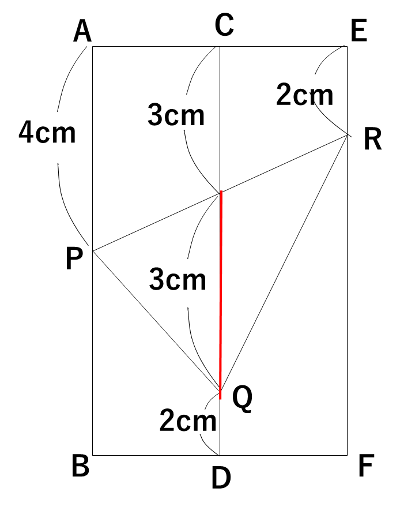
問題用紙にある図を利用して、下のように長さを書き込んでみます。
すると、赤い線の部分が3cmだと分かるので、底辺が3cm、高さが6cmの三角形の面積と同じになります。

（２）

点の移動の問題では、面積と時間の比例関係を利用する解法がよく用いられます。
（１）より、2秒後の面積が9㎠であることが分かっています。
ここで0秒後、つまり出発地点から動いていない時の三角形PQRの面積を求めると
6×8÷2＝24㎠　であることが分かります。これを表のようにまとめると

のようになります。ここから、2秒で面積が　24－9＝17㎠　減少していることが分かるので、1秒経つごとに8.5㎠　減少することがわかります。

これを利用して計算していきます。
「3点PQRが一直線に並ぶ」という表現を「三角形PQRの面積がゼロになる」と読み替えることがコツです。
24÷7.5＝3.2　より、3.2秒後に、三角形PQRの面積はゼロになり、したがって3点PQRは一直線に並びます。

（４）

この問題も、（３）と同じ考え方を利用して解くことができます。
注意が必要なのは、「考えられるもの全て」という点です。点PがBに到着して折り返すと、面積の変化が変わります。ここに注意すれば、2回とも答えを求めることができるでしょう。

大問７

（１）

いくつか試してみて、うまくいく組み合わせを探すという手法が良いでしょう。
答えは（1cm、11cm）と（5cm、7cm）に切った場合で、77㎠です。

（２）

18cmを（1cmと17cm）のように二つに分けるのですが、この際「互いに素」になるように切り分ければ良いです。この「互いに素」を利用した問題は、上位校でよく見かけます。頭の中で、すぐに引き出せるようにしておきましょう。
互いに素となる組み合わせは（1cm，17cm），（5cm，13cm）と（1cm，17cm），（7cm，11cm）と（5cm，13cm），（7cm，11cm）の3通りです。よって答えは　221㎠，187㎠，143㎠　の3つです。

（３）

Dの値が225とあるので、素因数分解してみましょう。
225＝17×5×3　ですので、17×15ではないかと予想を立てます。
一辺の長さとして、18から順に調べていくと、一辺が22cmの時に、互いに素の条件を満たすことが分かります。
よって答えは22cmです。

桐朋中学の算数入試問題は、作図による状況整理が必要な問題や、その場での思考力が必要な誘導問題などが特徴です。
これらの出題に対しては、通常の「問題を解く」とは少し違った思考法が必要となります。

通常は、問題が今まで勉強したどの解法に当てはまるか見分ける　→計算する
というような手順が一般的ですが、誘導問題などの場合は、

初めて見る問題設定を元に、いくつか具体例を書き出してみる　→規則・法則を見つける　→見つけた規則・法則を使って計算する

のように、試験のその場で法則を見つけるという手順が1つ加わります。
これは、典型問題の反復演習の延長線上にはない思考法で、過去問や、似た問題を出す他校の過去問などで、練習する必要があります。
通常の大手塾の模試では測りにくい能力です。
このような問題が解ける生徒に入学してほしいという、学校の先生たちからのメッセージを感じる出題です。例年出題の大筋は変わらず、学校としての軸がぶれていない証拠です。
きちんと対策し、入学したいという熱意を持った受験生には有利に働きます。是非過去問を入念に分析し、桐朋中学に必要な力を身に着けていきましょう。

著者：受験Dr. (受験ドクター)

この記事は役にたちましたか？