算数の合否を分けた一題（2019年度）

算数の合否を分けた一題

桐朋中入試対策・算数の合否を分けた一題（2019年度）

難易度分類

１	（１）A　（２）A　（３）A
２	（１）A　（２）A　（３）A
３	A
４	（１）A　（２）B
５	（１）A　（２）B　（３）B
６	（１）A　（２）A　（３）B
７	（１）A　（２）C

A…桐朋中合格を目指すなら、確実に得点したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難易度、処理量から判断して、部分点を拾えれば良しとする問題

問題別寸評

１

（１）～（３）分数・少数の計算問題です。

２

（１）

「15で割っても24で割っても」というところから、最小公倍数の120を利用することに気づくでしょう。気を付けるべきは、2019÷120＝16・・・119　から、
120×16＋7＝1927　と解答してしまわないようにすること。2019に「最も近い」なので、答えは　120×17+7＝2047です。

（２）

シャツが120枚ある。定価で売ったのは、その85％なので、120×0.85＝102枚になる。　2割引きで売ったのは、120-102＝18枚となる。　102枚を定価で売り、18枚を2割引き（0.8倍の価格）で売った場合の売上げ総額が93120円と問題文で示されている。
ここでは、シャツ1枚の値段を①とおくことで計算していきます。
108×①+18×①×0.8＝①×116.4　この①116.4＝93120円なので、　93120÷116.4＝800より、シャツ1枚の価格は800円です。

（３）

問題としては消去算の考え方を使います。消去するためには式を2本書く必要がありますが、2本目の式をどう書くか、で少し迷ったかもしれません。
男×1/5+女×3/14＝115人
上の式は比較的容易に書けますが、もう一本は　「ある中学校には560人の生徒がいる」というところから　男+女＝560　とすることがポイントです。次に、男の人数を1/5で揃えたいので、全体を1/5にした式を書きます。　男×1/5+女×1/5＝112人　とし、一本目の式と比べて消去することで解きます。

３

（１）

ニュートン算の問題です。この問題では、「牛1頭が1日で食べる草の量」を①と置くと考えやすいです。（似た問題ですと「チケット売り場1か所が1分で処理する人数」や「ポンプ1台で1分にくみ出す量」や「1人が1日でする仕事量」などがあります）
牛30頭が30日で食べた草の量は①×30×30＝〇×900　の草を食べています。
一方で、牛20頭が50日で食べた草の量は①×20×50＝〇×1000　です。
この差の〇×100の草は何かというと、30日で生えた草の量と50日で生えた草の量の差です。つまり、20日で生える草の量が、〇×100に相当するということです。　ここから、1日で生える草の量は〇×100÷20＝〇×5となります。（つまり牛が5頭までなら永遠に草牧草はなくならない計算になります）
さて、草を75日で食べつくすのに牛を何頭離せば良いかを計算するためには、あと「初めにはえていた草の量」を計算する必要があります。
牛30頭が30日で食べる草の量＝初めにはえていた量＋30日間で新たに生えた草の量
という式が成り立ちます。ここから計算すると
.①×30×30＝【初めにはえていた草】＋⑤×30
.①×900＝【初めにはえていた草】＋①×150
より、初めにはえていた草の量は①×750だと分かります。

よって、①×750＋5×75＝①×【牛の数】×75
となるため、計算して15頭となります。

４

(１)

平行四辺形BEFDの面積は、三角形BDCの面積の2倍に当たります。よって、
7×10÷2×2＝70㎠　です。

(２)

四角形BEFDは平行四辺形なので、 BDの長さとEFの長さは同じです。よって、BD：EC＝5：3です。相似を利用して、三角形AEDのADを底辺としたときの高さは、7㎝の8/5倍です。
よって　10×7×8/5×1/2＝56㎠　です。

５

合否を分けた一題で詳しく解説します。

６

（１）

問題文んの条件から、A列の1とC列の2を塗りました。この状態から3の列はどこに塗ることが出来るか考えていきます。
3は、「B,D,E,F」の4か所に塗ることができます。隣り合う2マスを塗らないように気を付けながら組み合わせを書き出していくと（B-D）（B-E）（B-F）（D-F）の4通りがあります。
よって考えられるNは（132300、132030、132003、102303）です。

（２）

Nを大きくするためには、なるべく左の位に大きな数を配置すれば良いです。そのためには、下の表のように塗れば良いです。

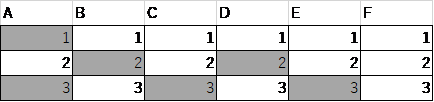
よってNは423230です。

（３）

A列の2が塗られているとき、Nが奇数になるためには①F列の1が塗られている②F列の3が塗られている。の2通り考えられます。
まず①のから検討していきます、この場合は下の表のようになります。

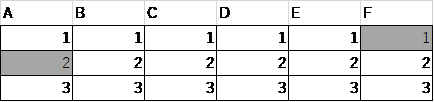
さて、3を3か所塗っていきますが、AとFに塗ることはできません（Aは2と隣り合ってしまうため。Fは塗るとNが偶数になってしまうため）
すると、B～Eの4か所に隣り合わないように3つ塗ることはできません。よって、このパターンは存在しません。
次に②を検討します。この場合は、下の表のようになります。

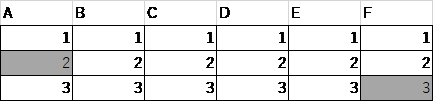
この表に、1を1か所、3を2か所に入れていきます。
まず先に3の塗り場所を考えます。隣り合わないように塗るには、BとDに塗るほかありません。
次に、1の塗り場所を考えます。1は、AとF以外どこに塗っても構いません。よって

ここまでが確定であり、後は1の塗り場所がB～Eの4か所から選べるので4通りあります。それぞれのNを計算すると（240303、231303、230403、230313）の4通りです。

７

（１）

図1の展開図の周りの長さは、a×4+3×8+2×2＝a×4+25
図2の展開図の周りの長さは、a×4+3×4+2×6＝a×4+24
よって差は1㎝です。

（２）①

周囲の長さが最も長くするためには、一番長い辺であるaが8本、次に長い3㎝が4本、最も短い2㎝が2本となる展開図にすればよいです。
よって　a×8+3×4+2×2＝44　となります。aは3.5㎝です。

（２）②

展開図の周の長さの組み合わせは、（8.4.2）（6,4,4）（4,4,2）の3通りあります。そのそれぞれにつき、長さを計算していきます。

合否を分けた１題

５

流水算の問題です。エンジンが停止しまた進み始めるなど変化の回数が多いですが、少しずつ変化を捉え、計算を進めていきましょう。

（１）

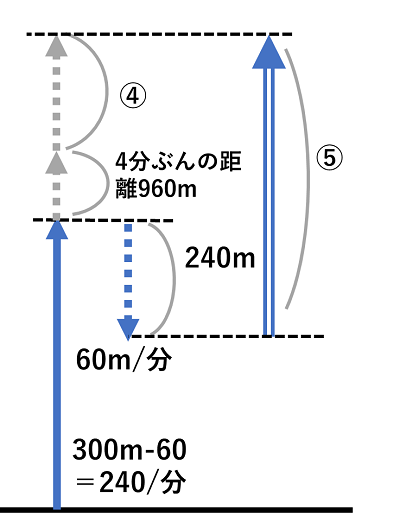
問題文を読んでいくと、船のエンジンが4分止まったために240m流されたということが分かります。この間は、流速のままに流されているので、流速は4分で240mです。よって、240÷4＝60

答え：毎分60m

（２）

線分図を描いて考えていきます。

図のように、④と⑤の差の①が240+960＝1200にあたるので、④は4800mです。
よって、エンジンが停止したのは、Q地まであと　4800+960＝5760mのところです。

答え：5760m

（３）

静水時の速さを分速300mにしてQ地からP地に戻ります。流速が分速60mなので、下りの速さは分速360mになります。
行きにかかった時間は、「はじめの速さで進み続けた場合と同じ」とあるので、300-60＝240　より、分速240mで進み続けたときと同じです。よって、上りと下りの速さの比は240：360＝2：3　となり、同じ距離を進むのにかかる時間の比は3：2になります。この2と3の差の1が時間の差の9分に当たります。よって、上りにかかった時間が9×3＝27分　下りにかかった時間が9×2＝18分です。　よってP地からQ地までの道のりは　360×18＝6480m　（別解：270×27＝6480m）

答え：6480m

著者：受験Dr. (受験ドクター)

この記事は役にたちましたか？