算数の合否を分けた一題（2016年度）

算数の合否を分けた一題

桐朋中入試対策・算数の合否を分けた一題（2016年度）

難易度分類

１	(1)　A　　(2)　A　　(3)　A
２	(1)　A　　(2)　A　　(3)　C
３	(1)　A　　(2)　B
４	(1)　A　　(2)　B　　(3)　B
５	(1)　A　　(2)　B
６	(1)　B　　(2)　B　　(3)　C
７	(1)　A　　(2)　①　A　②　B　③　C

A…桐朋中を目指すなら、確実に得点したい問題
B…知識・解法次第で得点に大きく差がつく問題
C…難易度・処理量から判断して、部分点を拾えれば良しとする問題

問題別寸評

１

(1)(2)(3)いずれも、基本的な計算問題です。ケアレスミスに十分に気を付け、確実に得点しなければならないところです。

２　小問集合

(1)

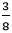男子× ＝女子×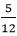 から、男子としかく女子の比は⑩：⑨をわかります。⑲が228人とわかれば、あとは男子の⑩にあたる人数をだせばおしまいです。

(2)

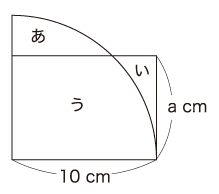
図のように、あ＝い　なので、あ＋う＝い＋う　となります。
あ＋うの面積は四分円で、その面積が　い＋うの面積と同じになります。

(3)

少し手間のかかる小問です。桐朋中は平成25年以降毎年、少し手間のかかる問題、かつ途中の過程を書かせる問題が出題されています。ここで、時間を取りすぎないように気をつけましょう。

等式の性質である、「＝」の左右で、同じものを付け加えたり、消したりしても、等式の関係はくずれないということを利用して考えていきましょう。
男子を□人、女子を〇人とした場合、
〇＋×＝31　…①
７×□＋８×〇―１＝鉛筆の本数　…②
６×□＋９×〇＋２＝鉛筆の本数　…③
と３つの式がつくれます。
②と③の式はともに鉛筆の本数ですので、②＝③といえます。

つまり、
　７×□＋８×〇―１＝６×□＋９×〇＋２
少し考えづらいので、等式の性質を利用し、「＝」の左右に＋１をして、
　７×□＋８×〇＝６×□＋９×〇＋３
と考えると、やりやすくなります。ここでまた等式の性質を利用し、「＝」の左右から６×□と８×〇を消してしまえば、
　１×□＝１×〇＋３　さらに、□＝〇＋３といえ、ここで①の式で□＋〇＝31でしたから、あとは和差算ですね。□＝17、〇＝14とでてきます。
よって男子の生徒は17人。
鉛筆の本数は②の式、③の式、どちらに式に□＝17、〇＝14をあてはめても、230本とでてきます。

平成22年の４でも似た問題が出題されていましたから。過去問をやりこんでいた生徒は断然有利だったといえるでしょう。

３　速さと比の問題

同じ距離すすむときは、「速さの比」と「かかる時間の比」は逆比になることを利用して解けば、容易にとけた問題です。

(1)

Aさんが16分ですすむところを、Bさんは車で２分ですすんだ、と気づけばあとは逆比の関係です。

(2)

BさんがAさんに２分で追いついてから８分でQ地に着いたので、P地からQ地までの4000ｍの距離を車だと10分で進んでいるので、車の速さは分速400ｍとなります。車と歩きの速さは８：１ですので、歩きの速さは分速50ｍとなります。

４　平均と面積図

面積図を書いて考えれば、（1）は容易にでてきます。（2）で少し混乱してしまうかもしれませんが、うまく切りぬければ、（3）は和差算で、この大問は（1）のみ正解だった生徒、（1）～（3）まですべてできた生徒と二分される問題だったかもしれません。この問題の（2）が合否をわけた問題の１つかもしれません。

(1)

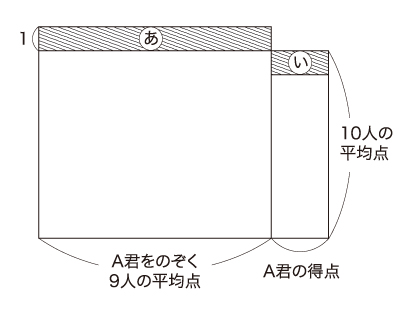
図のようにの部分の面積との部分が同じですので、１×９＝□×１。□＝９

(2)

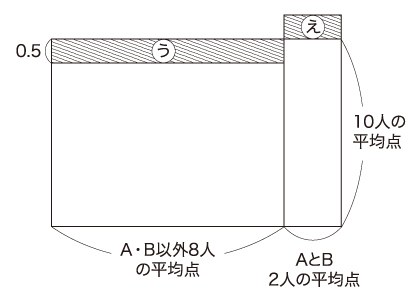
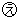(1)と同様に面積図を用いて考えます。の部分の面積との部分の面積が同じですので、の面積は0.5×８＝４。よっての部分の面積も４になります。

この４は10人の平均点よりA君とB君の得点の和が４点高いことを表しています。そして、A君は10人の平均点より９点低いことを（1）で求めたので、B君は10人の平均点より13点高くなければ、A君とB君の和が10人の平均点より４点高くなりません。
よって、B君とA君の得点の差は９＋13＝２２点となります。

(3)

(2)でA君とB君の差が２２点とだせれば、２人の平均点が７７点、つまり２人の得点の和は154点。和差算になりますね。

５　条件整理

(1)

カードの表面をA、　裏面aとします。どのような場合でも、A＋a＝18になるわけですので、

　表面　　A　B　 C　 D　 E　　…　　和は93
　裏面　　a　 b　 c　 d　 e　 …　　　和は177
　　　　　18　18　18　18　18　… 和は93+177＝270

よって、　270÷18＝15。15枚ならんでいることがわかります。

(2)

状況をしっかり書いていきましょう。単なる和差算になります。

　A　B　 C　　和は23
　　　　↓
　a　B　 C　　和は27
　　　　↓
　a　B　 c　　和は41　

上の式から、Aとaの差は４であることがわかります。また、Aとaの和は18ですので、すぐにでますね。　A＝７、a＝１１
さらに、Cとcの差は14であり、また、Cとcの和も18ですので、C＝2、c＝16。

よって、B＝14、b＝４とわかります。

一見、難しくみえる問題も、しっかり読んで、図にするなどすることにより、解法が見えてきます。

７　水量の問題

(1)

まずは入れた水の量を出しておきましょう。毎分24㎤の割合で、12.5分ですので、300㎤の水が水そうに入っています。
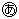と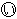の仕切りの高さ（仕切りア）の高さを□cmとしたとき、
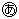の部分には、５×５×□　㎤
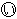の部分には、　３×５×５＝75㎤　
あといの部分で合わせて水は300㎤あるわけですので、
５×５×□＝225

よって□＝９　これが仕切りアの高さです。

(2)

①　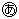、、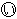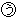の部分が同じ高さになったわけですので、仕切りをないものと考えましょう。水の量はこぼれていませんので、（1）のときと同じです。
②　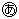、、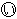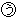の部分の入っている水の量は、底面積の比に等しいので、５：３：２となります。よって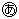の部分の水の量は150㎤。あとは底面積を台形のとみた四角柱の体積として考えていきましょう。（上底をa cm、下底は(1)で求めた仕切りアの高さです。）
③　最後の問題はなかなか難しい問題です。時間との兼ね合いでは、とれなくてもよい問題です。この問題を解ききるよりも、１などの見直し、各解答のチェックに時間をあてた方が得策といえるでしょう。

合否を分けた一題

６　図形の性質と場合の数

（1）

台形にとは「１組の向かい合う辺が平行になる四角形」ですので、ABとCDが平行、あるいはADとCBが平行になればいいわけです。そうすると、下の図のように４通りの台形がつくれることがわかります。△ABOと△CDOが相似、あるいは△ADOと△CBOが相似になるようにつくりあげる考え方でもよいと思います。

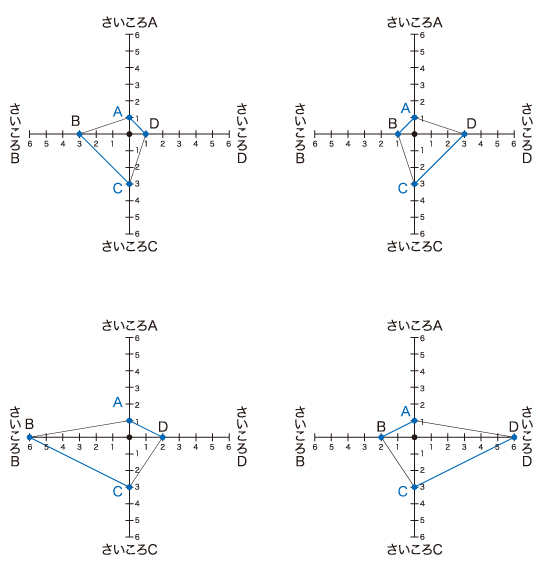
(2)

四角形の各頂点をABCDとしたとき、それぞれの四角形をBDで２つにわけ、上下の三角形でわけて考えてみましょう。）
面積を大きくするには、BD（底辺）をより長く、AO＋CO（AC）のそれぞれの高さもより長くしなればいけません。
それぞれの点は1,3,4,6ですので、考えられる組み合わせは

	BD	AC		□ABCD（△ABD＋△BDC）の面積
あ	１，３	４，６	→	４×10÷２＝20
い	１，４	３，６	→	５×９÷２＝22.5
う	１，６	３，４	→	７×７÷２＝24.5
え	３，４	１，６	→	７×７÷２＝24.5
お	３，６	１，４	→	５×９÷２＝22.5
か	４，６	１，３	→	４×10÷２＝20

の６通りしかありません。それぞれの面積をだせば、「う」と「え」の面積が最大になることがわかります。
また、ここで、□ABCDの面積がBD×AC÷２で求められることに気がつけば、（3）をうまく解くことができます。

（3）

（2）で使った考え方を利用しましょう。「うまく誘導にのる」。桐朋中だけに限りませんが、いわゆる誘導問題の代表的なパターンの１つです。身に着けておきたい発想です。

さて、いま与えられている条件がA＝１、B＝２となっています。また、面積が12cm2ですので
　BD×AC÷２＝12　つまり、BD×AC＝24になるような組み合わせを考えましょう。
さいころの目ですので、長さは必ず整数です。したがって、
１×２４、２×１２、３×８、４×６、６×４、８×３、１２×２、２４×１が考えらます。
そのうち、BDの長さは少なくとも３ｃｍ、（ＢＯが２cmなので、少なくともOBは１cmになるので。）同様に、ACの長さは２cmになるので、上のかけ算のうち、
　３×８、４×６、６×４、８×３、１２×２の５通りしか考えられません。
ここで、表にまとめてみますと、

	BDの長さ	ACの長さ		ODの長さ	OCの長さ	条件に…
あ	３	８	→	１	７	×（さいころの目は６まで）
い	４	６	→	２	５	○
う	６	４	→	４	３	○
え	８	３	→	６	２	○
お	１２	２	→	１０	１	×（さいころの目は６まで）