算数の合否を分けた一題（2015年度）

算数の合否を分けた一題

桐朋中入試対策・算数の合否を分けた一題（2015年度）

難易度分類

１	(1)　A　(2)　A　(3)　A
２	(1)　A　(2)　A　(3)　A
３	B
４	B
５	(1)ア　A　イ　B　(2)　A　(3)　C
６	(1)　B　(2)　B
７	(1)　A　(2)　B　(3)　C

A…桐朋中を目指すなら、確実に得点したい問題
B…知識・解法次第で得点に大きく差がつく問題
C…難易度・処理量から判断して、部分点を拾えれば良しとする問題

平成２７年　問題別寸評

１

(1)(2)(3)いずれも、基本的な計算問題です。ケアレスミスに十分に気を付け、確実に得点しなければならないところです。

２　小問集合

(1)　「３つのつるかめ算」と思い、解き始めた生徒は多いかもしれません。しかし、条件をしっかり読み取れば、１円玉、５円玉、10円玉の枚数の比が連比で求められることがわかります。１円玉：５円玉：１０円玉の枚数の比は⑬：⑨：①となり、その枚数を１セットにします。金額は1×⑬＋5×⑨＋10×①＝68円となり、1972÷68＝29セットつくれます。１セットの中に10円玉は１枚ですから、29セットで29枚とわかります。
(2)　等積変形の基本となる部分の問題です。Eを通るAD、ECに平行な線を入れて、ABCDの面積の半分が17＋13＝30㎠であることに気がつけば、あとは容易ですね。
(3)　通過算の典型的な基本問題です。２つの条件の距離と時間の差に注目し、まず、電車の秒速を出しましょう。秒速がでれば、あとは（電車の秒速）×（秒数）で電車の進んだ距離をだし、電車の進んだ距離―鉄橋の長さで電車の長さを出せます。

３　倍数変化算

倍数変化算を同じものに注目し、その比をそろえるのが鉄則です。また、分数がでてくると、解きづらくなる生徒も多いので、整数化して考えていくことが、より速く、より確実に解けることでしょう

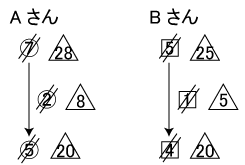
Aさんの最初の所持金を⑦、Bさんの最初の所持金を５とすると、下の図のような状況図が書けます。

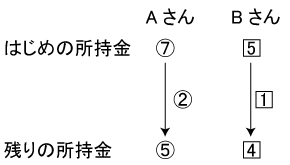
②＝ノート８冊分、１＝ノート5冊分ですか、ノート１冊は0.25＝0.2となりますので、この比をにそろえると、さらに下のようになります。

＝2650円ですから、＝50円とわかり、Aさんの所持金が求まります。

４　３人の仕事算

AとB、BとC、CとAの１分あたりの仕事量をだすと、∶∶となり、８：７：９となります。そこから、１分あたり、A＝５、B＝３、C＝４の仕事量と求められ、全体の仕事量を504と表せられます。あとは３人で１分あたり12できるので、504÷12＝42（分）、と出てきます

５

(1)　円周を12等分しているので、中心角１つ分は30度となりますね。は∠BOD＝60°なので、△BODは正三角形ですので、60°とわかります。はOKに補助線を入れてあげれば、△OKBは直角二等辺三角形となりますね。△KLBに注目しすぎて、苦戦してしまった生徒もいるかもしれません。
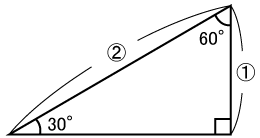
(2)　30°、60°、90°の直角三角形は下の図のような、辺の長さに関係があります。

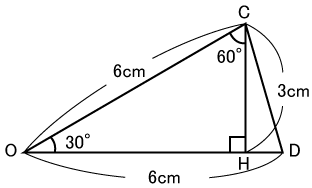
そうすると、下の図のように、Cから辺ODに垂直な線分を入れると、30°、60°、90°の直角三角形ができます。いま、CはODにひいた垂直な線との交点をHとすると、CHは３cmとわかります。

よって三角形CODは６×３÷２＝９㎠とわかります。

(3)　「合否をわけた１題」に詳しく記載します。

６

ろうそくの燃え方の問題ですが、速さと比の問題としてとらえられれば、難しくはない問題です。
(1)　がｘcmの部分がすべて燃えたとき、の素材Bの部分がまだ５cm残っているということは、の方はｘcmの部分が燃え尽きるまであと30分かかることがわかります。また、素材Aの部分を進む火の速さ：素材Ｂの部分をすすむ速さの比は③：②になりますので、かかる時間は逆比の２：３。その差の１が30分にあたりますので、がxcm燃えるのに60分、がxcm燃えるのに90分かかることがわかります。つまり、の方は４分で１cm燃えるので、60分で15ｃｍ。（同様にの方は６分で１cm燃えるので、90分で15cmと同じ答えが出てきます。）
(2)　ycmの方も同様に考えていけば、ろうそくの方が30分先に燃え始め、14分早く燃え尽きたということは、30－14＝16分の差が縮まったことになります。
(1)と同じく、素材Aの部分を進む火の速さ：素材Ｂの部分をすすむ速さの比は③：②になりますので、かかる時間は逆比の２：３ですので、今度は1＝16分となり、のろうそくがｙcmの部分を燃やすのに48分、のろうそくがｙcmの部分を燃やすのに、32分かかります。のろうそくは素材Bの部分なので、48分で48÷6＝８cm。（同様に、のろうそくは素材Aの部分なので、32分で32÷4＝8cmと同じ答えが出てきます。）

このような初めて見るような問題、あるいはふだん見慣れた問題とは少し違うというときに、冷静に「これはどのような解法で解いていくか」を考える力を求めています。桐朋中に限らず、身に着けておきたい力です。

７　立方体の展開図の関する問題

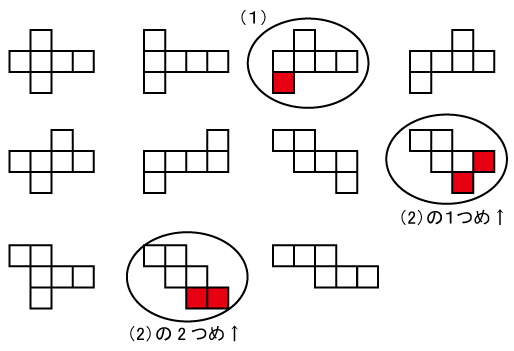
立方体の展開図は下の図のように11種類あります。
(1)　〇で囲んだの展開図の(1)を選び、赤でぬった部分を付け加えればOKです。
(2)　すでにぬられている４カ所の和は８ですので、あと２つの面で７をつくればよいです。７は３＋４と２＋５のいずれかが可能ですが、５の部分を利用した展開図はつくれませんので、３と４の２つの面を利用した展開図を考えます。そうすると、〇で囲んだ展開図(2)の２つがつくれます。赤でぬった部分を付け加えればOKです。の２つあるので、どちらかが思いつきづらいかもしれません。

(3)はまず、どのような展開図が可能か、さらに、太い線が重なるかを考えていかなければならない、処理する量が非常に多く、この問題は見送ってしまってもよいでしょう。

合否を分けた１題

今年度の入試問題も例年通り大問７題の構成でした。また、構成も１の計算問題、２の小問集合、３以降の大問は、速さ、平面図形、割合等の文章題、整数問題、思考力系の問題となっており、傾向も難易度も例年通りでした。見た目簡単に見える問題でも、いざ解いてみると、素直に難しい問題もあり、よく練られた入試問題といえるでしょう。

さて、今年度の入試問題でこの問題がまさに合否をわけたと思われる問題を紹介します。
５の(3)です。　桐朋中のお家芸ともいえる良問です。

△LOBの面積も、△LKBの面積も出せないけれど、差は出せるという問題です。
過去にも、四角形の４辺の長さが一部何cmか出せないけれど、２つの四角形の４辺の長さの差なら出せるという問題が出題されました。（平成18年の６）過去問をよく研究した生徒なら、解法の糸口がみつけられたかもしれません。

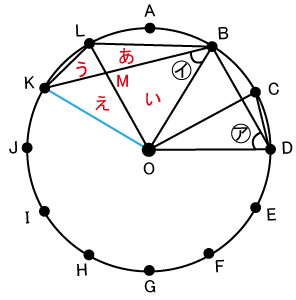
toho-6

いま、ＯＫに補助線を入れてみましょう。そうすると、△ＯＢＫは直角二等辺三角形だとわかります。また、△ＯＢＬは正三角形、△ＯＫＬは二等辺三角形とわかります。さらに、△ＯＫＬは(2)で求めた△ＯＣＤと合同ですので、面積は9cm2とわかります。

さて、本題に入ってきましょう。上の図のように、あ、い、う、えと４つの三角形にわけたとき、△LOBはあ＋い。△LBKはあ＋うになります。つまり、△LOBと△LBKの面積の差は「い」と「う」の差になります。
また、△OBKは直角二等辺三角形は６×６÷２＝18cm2で、△OKLは(1)で求めた△OCDと同じですので、９㎠。△OBKはい＋え。△OKLはう＋え。２つの三角形の差は、いとうの部分であり、差は18―9＝９cm2。よって、△LOBと△LBKの差も９㎠とわかります。

著者：受験Dr. (受験ドクター)

この記事は役にたちましたか？