算数の合否を分けた一題
早実中等部入試対策・算数の合否を分けた一題(2021年度)
難易度分類
| [1] | (1) A (2) A (3) B (4) B |
|---|---|
| [2] | (1) ① A ② A (2) A |
| [3] | (1) A (2) A (3) B |
| [4] | (1) ① A ② B (2) C |
| [5] | (1) B (2) ① B ② C |
A:早稲田実業合格を目指すなら必ず得点したい問題
B:着眼点や解法ツールにより正答率・かかる時間に差がつく問題
C:難易度や処理量から判断して、後回しにすべき問題
出題総評
いわゆる「難問」というものはほとんどありませんでしたが、典型的な問題に関する解法知識やコツを知らないと時間が掛かってしまう問題が数多く見られました。
また、最初の計算問題では、2018年度以降4年連続で、分母が8である分数と見間違えやすい小数を式の中に入れており、過去問をしっかりやってきた受験生ならすぐに気づくようなひっかけ問題になっています。これは、併願校として受験する生徒ではなく、本校を第一志望として受験する生徒が欲しいという学校側の意思の表れでしょう。
それだけに、問題数や基本的な構成も例年を踏襲しており、過去問を練習してきた受験生にはおなじみの出題だったと思います。
問題別寸評
人気校の受験生にとっては基本的な問題を、少しずつひねり、視点を変えて出題している印象の小問集合です。特に(3)や(4)については、人によって所要時間にかなり大きな差ができたと思います。ここでの所要時間の差は、後半で使える時間の差となったり、計算に使える時間の差になったりして、間接的に入試問題全体の出来不出来に影響を及ぼすおそれもあります。
短時間で正確に解ける解法を身につけておきましょう。
(1)
一昨年の「1.675」、昨年の「0.675」に続き、今年もうろ覚えを許さない数字を入れてきました。過去問をしっかりやってきた受験生にはおなじみ……とすることで、第一志望校として受ける生徒が有利になるように工夫しているのかもしれません。
「1.325」を「1と8分の3」(1.375)と間違わないように気をつけてください。
(2)
連比を使ってBとCの歯数の比を求め、その逆比をとるだけの基本問題です。
(3)
正方形の対称性に気づけば非常に易しい問題なのですが、その視点が持てなかった受験生には「どうしてもそこだけ求まらない」という印象になったかもしれません。テスト序盤で解けない問題に遭遇するとかなり動揺しますので、精神的なものも含めると、これが「合否を分けた一題」になってしまった可能性もあります。
(4)
立体的な影の形を正確に想像できたでしょうか。同じ立体でも、これが回転体の体積として出題されたなら多くの受験生にとって見慣れた問題になりますので、解法の違いによって正答率や所要時間に差が出たかもしれません。
大問[2]全体としては小問集合のような体を取っていますが、実質的には(1)だけで一つの大問というような構成です。
また、(2)は、今年の西暦年である「2021」を、連続する「20」「21」という2つの整数に分けてとらえたところまでは、同じく今年の駒場東邦中学の大問[4]で出題された問題とも似ていましたが、その後の切り口はかなり異なっています。
いずれも、実質的にはそれほど難しいわけではありませんが、先入観にとらわれずに問題の本質を見抜けるかどうかが鍵となる問題でした。
(1)
一見すると、通過算と流水算を融合させた問題でした。しかし、①では、速さ差を考える場合も、速さの和を考える場合も、流れの速さは相殺されてしまうので影響しません。また、②では、同じ距離を上る場合の速さの比だけで考えることができるので、船の長さが影響しません。つまり、本質的には①がただの通過算で、②がただの流水算だったと言えます。
(2)
実際には数字を拾っていくだけなので、駒場東邦中学の問題よりもこちらの方が簡単です。
しかし、「1234(1と2と3と4)」を数え忘れなかったかどうかで明暗が分かれた可能性があります。また、数えもれがないよう丁寧に探すしか方法がないので、解く順序としては後回しにしても良い問題だったかもしれません。
国語と算数の複合表になっていますが、表の見方さえ理解できていれば(1)は易問ですし、(2)の計算には算数の得点しか使いませんので、見慣れた問題とほとんど変わりません。
(1)
「算数より国語が高い」ですので、判明していないア,イの数値はいずれも不要です。
(2)
算数の得点だけで表を作り直せば、一度は解いたことのあるつるかめ算の典型題と変わりません。
(3)
本問を、「合否を分けた一題」として詳しく後述します。
数字ゲームの必勝法に関する問題は、様々な学校の入試で、論理思考の問題としてしばしば出題されています。当然、規則性はありますので、それを読み取れるかどうかが鍵となります。
(1)
①は、規則性に気づかせるための誘導問題です。調べ上げるしかないとはいえ、この問題を解かないと規則性がつかめず、後の問題も解けなくなってしまいます。小さい数なのでそれほど時間はかかりませんから、実際に書き出して調べましょう。①の結果から、フィボナッチ数列になっていることに気づけたでしょうか。
(2)
B君にとっての必勝法というのは、「3の倍数で終わらせること」です。論理思考に慣れていないと、必勝法の発見に時間がかかってしまうかもしれません。思いつかなければ早めに見切りをつけて後回しにしましょう。
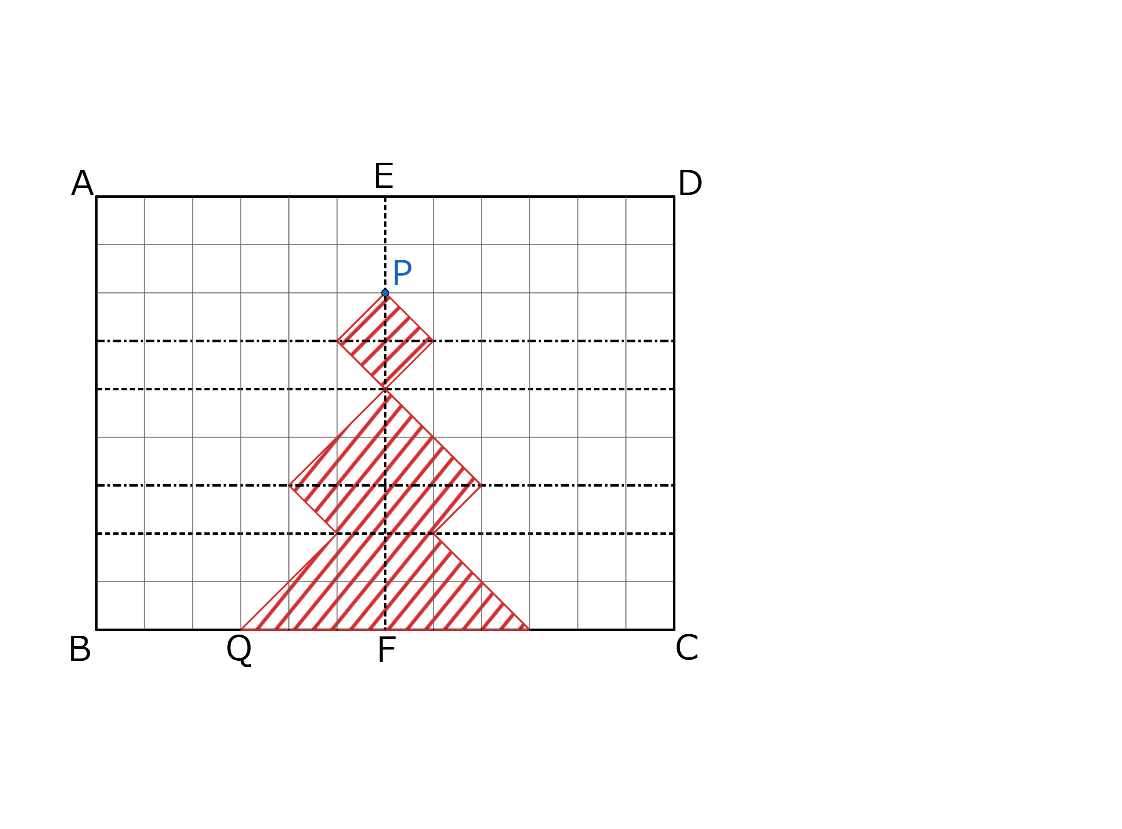
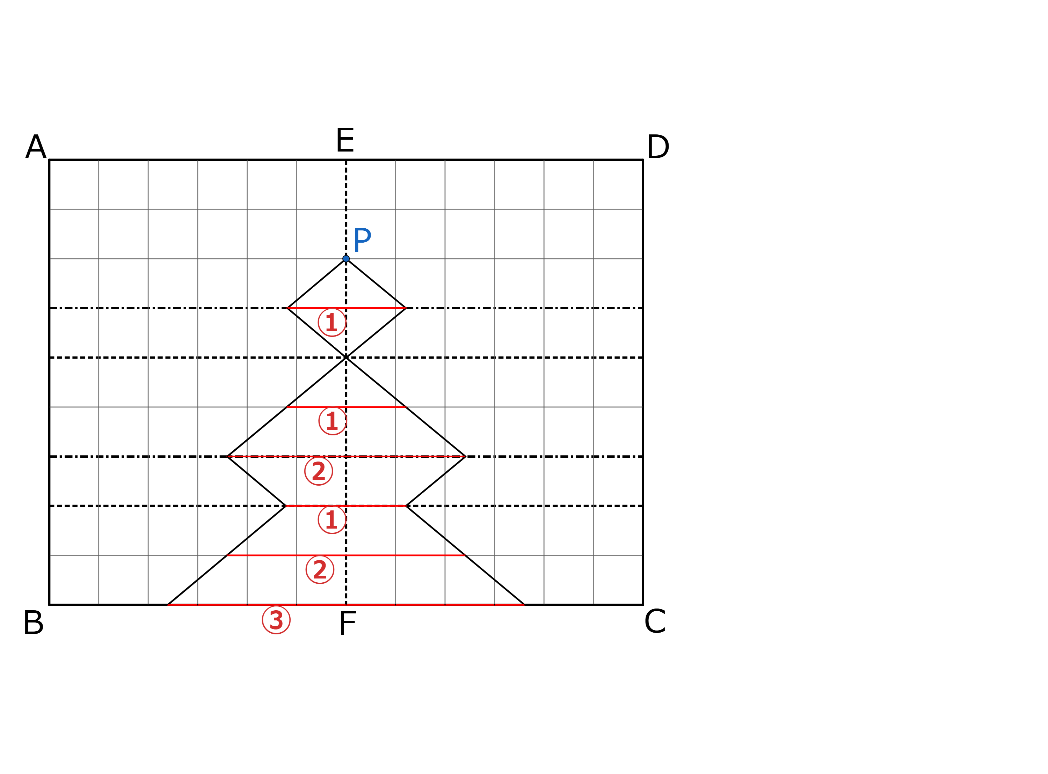
折り返しの問題を解くには、対称性を利用するのが定石です。イメージするのが難しい部分は、与えられた図を利用して考えましょう。
(1)
落ち着いて考えれば難しくありませんし、ここで間違えると(2)も全滅しますから、確実に正解してください。山折りでも谷折りでも、折り目を軸に、切断する場所は線対称になります。
(2)
対称性を利用して切り取られた部分を図示すると、①は左下の図のようになります。
また、②は、右下の図の部分の長さの比が1:2:3になることを利用して、たて1cmごとに区切った三角形または台形の面積比を求めます。
合否を分けた一題
気づいてしまえば、実際にはさほど難しくないのですが、論理思考に慣れていない受験生には難しく感じたと思います。
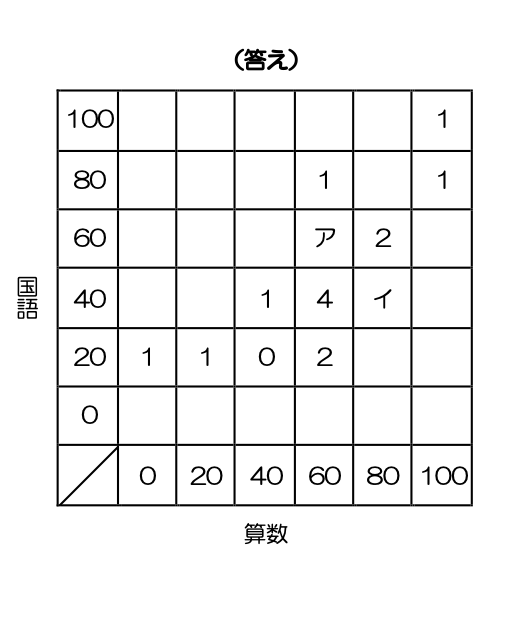
まず、再試験前に57点だった算数の平均点が62点になったことから、全員の合計点は
(62-57)×20=100点
と、100点増加したことが分かります。
ここで鍵となるのは、表1で1人だった「算数40点・国語20点」の人が、表2では0人になっていることです。
つまり、再試験で60点以上をとった3人のうちは1人がこの人だということになり、その場合は60点扱いになりますので、この一人だけで40点から60点へと20点分増加しています。
そうなると、残り2人であと80点分合計点が増えることになります。
さて、再試験を受けた40点以下だった人の得点の上がり方は、60点(0点→60点)、40点(20点→60点)、20点(40点→60点)のいずれかですので、2人で80点増加するためには、
① 40点 + 40点 = 80点
② 60点 + 20点 = 80点
の2通りしか考えられません。
しかし、最初の試験で算数が20点だった人が1人しかいないことから、2人の人が40点ずつ増加する➀のパターンは不可能であることが分かります。
また、最初の試験で40点だった人のうち、国語が40点だった人が2人、国語が20点だった人が1人いますが、表1で1人だった「算数40点・国語20点」の人が、表2では0人になっているという条件から、もう一人は国語が40点だった2人のうちの1人と確定できます。
つまり、下の表の●印の部分にあてはまる人が1人ずつ60点に変われば正解です。
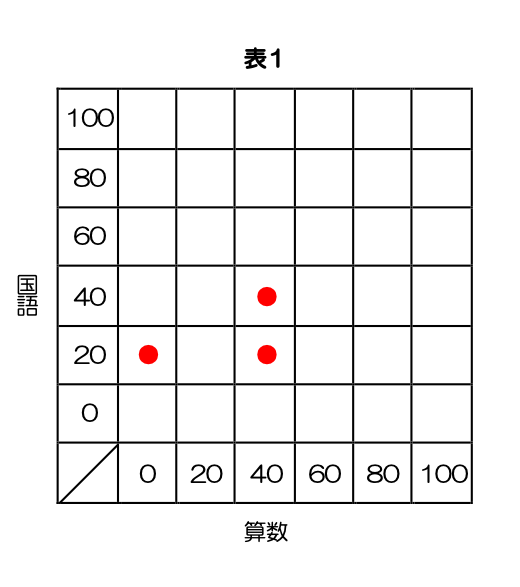
どの欄の数字がどのように変わるのか、ミスのないように埋めてください。
早実中等部入試対策・関連記事一覧
早実中等部入試対策・同じ教科(算数)の記事
早実中等部入試対策・同じテーマ(合否を分けた一題)の記事
- 算数の合否を分けた一題(2012年度)
- 算数の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2016年度)
- 国語の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2016年度)
- 理科の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2018年度)
- 国語の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2018年度)
- 国語の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2019年度)
- 社会の合否を分けた一題(2019年度)
- 国語の合否を分けた一題(2020年度)
- 算数の合否を分けた一題(2020年度)
- 理科の合否を分けた一題(2021年度)
- 国語の合否を分けた一題(2021年度)