算数の合否を分けた一題（2020年度）

算数の合否を分けた一題

早実中等部入試対策・算数の合否を分けた一題（2020年度）

難易度分類

［1］	(1)A　(2)A　(3)A　(4)A
［2］	(1)①A　②A　(2)①A　②A
［3］	(1)A　(2)B　(3)B
［4］	(1)A　(2)B　(3)C
［5］	(1)B　(2)B　(3)C

A：早稲田実業合格を目指すなら必ず得点したい問題
B：着眼点や解法ツールにより正答率・かかる時間に差がつく問題
C：難易度や処理量から判断して、後回しにすべき問題

出題総評

今年も例年通り、大問1は計算問題を含む小問が4つ、大問2は小問が2×2=4つ、大問3・4・5は各単元にわかれての形式でした。
詳細については大問1が計算1問＋小問3問（割合・場合の数・立体図形）、大問2は速さ・割合2問と規則性2問、大問3は速さとダイヤグラムの問題、大問4は割合の応用問題、大問5は平面図形の応用問題でした。

問題別寸評

［1］

どの問題も本校に合格するためには落とすことは出来ません。時間の目安としては7分ほどです。

(1)

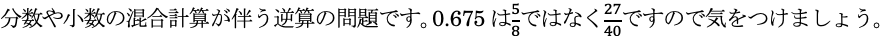
(2)

割合から、相当算の文章題です。仕入れた商品の個数を①個とおき、線分図を描いて整理をしていくようにしましょう。

(3)

場合の数から、道順の問題です。全部の道順の場合の数から×印のある部分を通る場合の数を引くより、×印を通らない場合の数を直接求める方が効率的です。

(4)

EGとFCを延長した時に交わる点をIとし、DとIを結んだ直線がACと交わる点をHとします。Aを含まない立体は、三角錐I-DEFから三角錐I-CHGを引いたものになります。各々の立体の体積を直接求めてもよいですし、体積比を用いてもかまいません。全体の三角柱から、Aを含まない立体を引けば答えが求まります。

［2］

どちらも各単元の標準的なレベルの小問群で、すべて正解したいところです。

(1)

②うの角度が18°であるので、短針が0分の状態から18÷0.5=36分進んだことになります。また、あの角度が①=6°であることから、長針の進み方を考えると6÷6=1分、36-1=35分から長針のすぐそばの文字盤は7であることも分かり、答えが求まります。

(2)

［3］

ここからは、単元ごとの大問になります。速さとダイヤグラムの問題です。今年は本問を、合否を分けた一題として詳細を後述します。

［4］

仕事算と食塩水の融合問題です。

(1)

問題文3・4行目の条件から仕事算として処理します。48と18の最小公倍数である144Lを水そういっぱいの量とすると、菅Aは1分あたりに144÷48=3Lの食塩水を入れ、菅A・Bの両方で1分あたりに144÷18=8Lの食塩水を入れることになります。ここから、菅Bが1分あたりに入れる食塩水の量がわかるので答えも求まります。

(2)

(3)

［5］

最後の大問にして、直角三角形の相似を利用する応用問題です。直角三角形相似は、互いに対応する辺を取り違えないよう、□(直角)・〇・×の記号を必ずふるようにしましょう。

(1)

まず、最も小さい半円の半径の長さを①とすると、AB=③、AC=④、AD=⑤となります。次に四角形ABCDは平行四辺形なのでBC=AD=⑤です。三角形ABCに着目し、角BACは直角なので□、角ABCを〇、角ACBを×とします。さらにEからABに向かって垂線をおろし、ぶつかった点をJとすると、三角形ABCと三角形JBEは相似、EA=EBであることから三角形JBEと三角形JAEも相似、三角形ABCと三角形JAEが相似であることがわかります。ここから角AEJは×であり、ACとJEが平行であることから錯角を利用すると角AEJ=角FAGなので×です。したがって角FGAは〇となり、三角形AFGも相似であることになります。対頂角を利用すると角FGA=角CGDなので〇です。三角形CDGに着目すると、角CDGは×となって相似となります。ここからCD:CGが求まります。
三角形ACD・三角形CDGを見てみるとDC:CA=3:4、GC:DC=3:4なのでDCを3と4の最小公倍数である12にそろえます（比を合わせます）。ここからCG:GAも求まります。

(2)

対応する辺同士を較べるとBC:AG=20:7なので、ここから相似の面積比を利用すると、2つの三角形の面積比が求まります。

(3)

合否を分けた一題

今回は、大問3について合否を分けた一題として紹介しましょう。歩数と歩幅、速さの関係の知識の整理から始まり、3人の動きを与えられたダイヤグラムから読み取って比を利用する重要な問題であると言えます。

［3］旅人算・ダイヤグラム

(1)

問題文1・2行目の条件から太郎君と次郎君の歩幅の比が4:3、歩数の比が5:6なので、歩幅×歩数=速さの知識を利用すると4×5:3×6=20:18=10:9となります。
答え：10:9

(2)

ダイヤグラムを見てみると、花子さんがAからBまで進む間に太郎君がABを往復しています。ここから、太郎君と花子さんの速さの比は2:1となります。時間一定であれば速さ比と進んだ距離比が同じになることを利用すると、3人とも同時に出発しているのでAC:BC=太郎君の速さ:次郎君の速さ=10:9、AD:BD=太郎君の速さ:花子さんの速さ=2:1です。ABの距離を10+9=19と2+1=3の最小公倍数である57とする（比を合わせる）と、AC:CD:DB=30:8:19となるのでAB=80×57/8 =570ｍとなります。
答え：570ｍ

(3)

答え：3分10秒後