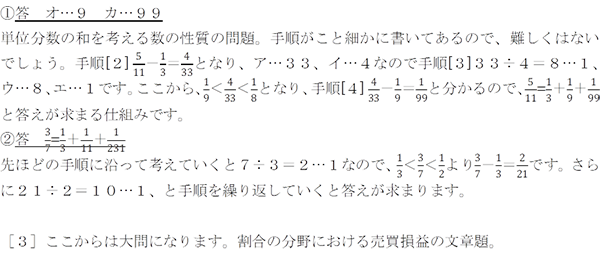算数の合否を分けた一題（2019年度）

算数の合否を分けた一題

早実中等部入試対策・算数の合否を分けた一題（2019年度）

難易度分類

［１］	(1)A　(2)A　(3)A　(4)B
［２］	(1)B　(2)A
［３］	(1)A　(2)A (3)B
［４］	(1)A　(2)A (3)C
［５］	(1)A　(2)B　(3)B　(4)C

Ａ：早実合格を目指すなら必ず得点したい問題
Ｂ：着眼点や解法ツールにより正答率・かかる時間に差がつく問題
Ｃ：難易度や処理量から判断して、後回しにすべき問題

出題総評

大問１は計算問題を含む小問が４つ、大問２は小問が２つ、大問３・４・５は各単元にわかれての形式でした。
詳細については大問１が計算１問＋小問３問（場合の数・植木算・年齢算）、大問２は立体図形１問と数の性質１問、大問３は割合（売買損益）の問題、大問４は平面図形（相似の応用）の問題、大問５は点の移動の応用問題でした。

問題別寸評

[１]

(1)　答　１５

分数や小数の混合計算を使う逆算の問題。１．６７５は15/8ではなく127/40であることに注意してください。工夫は特にないので、分数に統一して慎重に・順番に計算していきましょう。２分以内に終わらせるのがベストです。

(2)　答　１４個

カードを並べる場合の数の、典型的な一行問題。十の位の数字で場合分けすると□４□、□３□、□２□となります。それぞれ、３×３＝９個、２×２＝４個、１×１＝１個あります。なお、□１□は問題文の条件に反するのでありません。

(3)　答　２．４㎞

木の植え方を変える植木算の典型題。５０ｍおきと３０ｍおきとでは、それぞれの間隔の長さが５０：３０＝５：３です。どちらの条件でも池の周りは同じですので、間隔の数の比は逆比で３：５となります。よって、その比の差である５－３＝２が３２本となるので、５０ｍおきでは３２÷２×３＝４８本、３０ｍおきでは３２÷２×５＝８０本植えたことになります。ここから距離が求まります。（なお、５０と３０の最小公倍数である１５０ｍを仮の距離とすると、差は１５０÷３０－１５０÷５０＝２本となり、距離も３２÷２＝１６倍になる、と考えても良いでしょう。）

(4)　答　３４才

［２］

(1)　答　２８．８㎤

展開図が与えられており、それを組み立ててできる立体の体積を考える問題。展開図の真ん中にある五角形を底面とすると、下図のような立体になります。

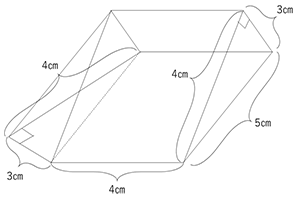
長方形を底面とする三角柱は、３×４÷２×４＝２４㎤です。また、図の左側にある三角すいですが、高さは三辺が３㎝・４㎝・５㎝の直角三角形の、５㎝を底辺としたときの高さと同じなので、３×４÷５＝２．４㎝です。三角すいの体積は４×３÷２×２．４÷３＝４．８㎤となります。先ほどの三角柱との合計で答えが求まります。

(2)

［３］

ここからは大問になります。割合の分野における売買損益の文章題。

(1)　答　８０個

(2)　答　８００円

Ａについて、定価は仕入れ値より４００円高く、問題文５～６行目より売値は仕入れ値より１６０円高いので、定価を４００－１６０＝２４０円値引きして売値をつけたことになります。問題文５行目の条件から、値引き額は定価×０．２＝２４０円となるので、Ａの定価は求まり、そこから原価も求まります。

(3)　答　４０個

Ｂは８０個すべて売れたので、利益の合計は３００×８０＝２４０００円です。問題文６～７行目の条件から、Ａの利益の合計は２４０００÷５×８＝３８４００円です。Ａについて、定価で売った場合は１個当たり４００円の利益があり、売値で売った場合は１個当たり１６０円の利益があるので、全体の個数が１２０個であることからつるかめ算を用いれば答えが求まります。

［４］

補助線を引きながら、面積比や図の中の相似を考えていく三角形を題材とした平面図形の問題。

(1)　答　６：１

Ａ、Ｃから正面の辺に向かって線が引いてあり、交点がＲとなっています。そのＲを通るようにＢからも線を引くと、以下のようになります。

△ＡＢＲ、△ＡＲＣ、△ＢＲＣの３つにわかれます。（自動車のベンツのマークや三ツ矢サイダーのマークに似ているので、このテクニックを「ベンツ切り」と呼ぶことがあります。）
ＢＤ：ＤＣ＝２：１なので、△ＡＢＲ：△ＡＲＣ＝２：１です。ＡＦ：ＦＢ＝２：１なので、△ＡＲＣ：△ＢＲＣ＝２：１です。ここから連比をとると△ＡＢＲ：△ＡＲＣ：△ＢＲＣ＝４：２：１となります。ＡＲ：ＲＤは（△ＡＢＲ＋△ＡＲＣ）：△ＢＲＣと同じですので答えが求まります。

(2)　答　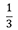倍

(1)の答えから、△ＡＲＣ：△ＣＲＤも６：１です。両者を合計した７が△ＡＤＣとなり、ＢＤ：ＤＣ＝２：１であることから、全体の面積である△ＡＢＣは７×（１＋２）＝２１ということになります。△ＡＲＣ、△ＢＰＡ、△ＣＱＢは全て６なので、△ＰＱＲは２１－６×３＝３ということなります。△ＡＰＥは△ＣＲＤと合同ですから、答えが求まります。

(3)　答　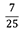倍

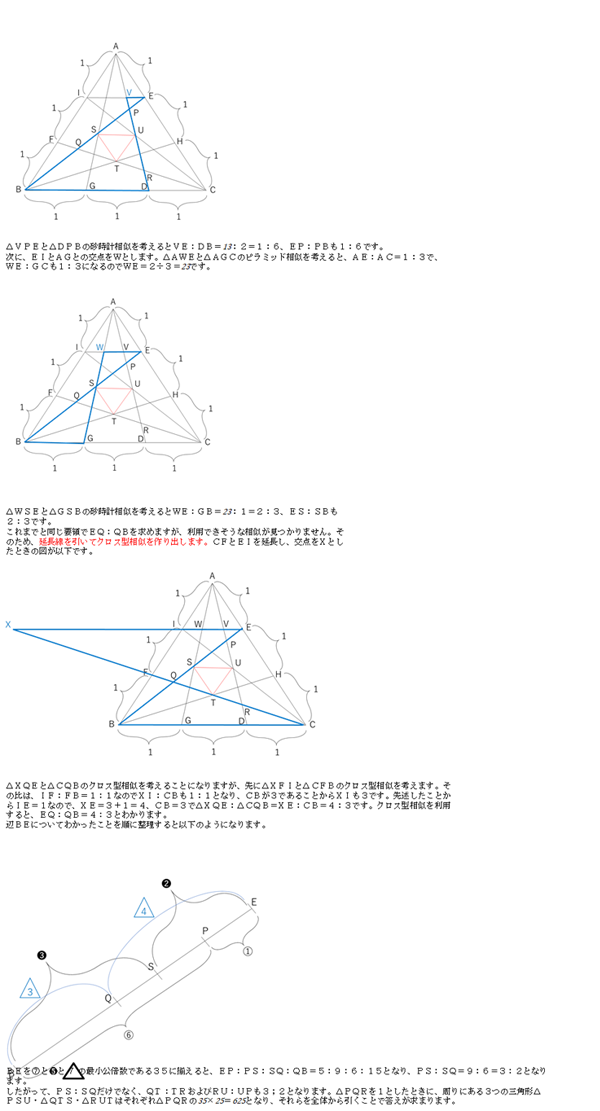
補助線を引いてクロス型相似を作り、さらに比を合わせていくことを考えねばならない難問です。△ＳＴＵが△ＰＱＲの何倍であるかを問われているので、△ＰＱＲから周りの三角形である△ＰＳＵ・△ＱＴＳ・△ＲＵＴを引くことを考えます。そのために、ＰＳ：ＳＱを、相似を使って求めます。（なお、ＰＳ：ＳＱもＱＴ：ＴＲもＲＵ：ＵＰも図形の対称性から全て同じ比となります）
まず、ＥからＩに向かって直線を引き、ＡＤとの交点をＶとします。△ＡＶＥと△ＡＤＣのピラミッド相似を考えると、ＡＥ：ＡＣ＝１：３で、ＶＥ：ＤＣも１：３になるのでＶＥ＝１÷３＝です。

［５］

最後の大問であり、２点が円周上を移動する点の移動および周期算の問題。今年は本問について合否を分けた一題として後述します。
(1)答　１９２°
(2)答　２４°
(3)答　４倍
(4)答　１３回

合否を分けた一題

今回は、最終問でありながら、得点するべき箇所のあった大問５を、合否をわけた一題として紹介しましょう。２点の動きについてしっかりと進む方向をイメージしなければならず、点の移動の応用的な考え方として良い問題と言えます。

［４］点の移動・規則性

(1) ＡＣ＝ＢＣとあるので、円の中に二等辺三角形を作ることを考えます。円の中心であるＯからＣに向かって線を引くと

円の半径でＯＡ＝ＯＢ＝ＯＣ、さらにＡＣ＝ＢＣなので△ＯＡＣと△ＯＢＣはどちらも合同な二等辺三角形であることがわかります。角ＡＣＢが８４°なので、角ＯＣＡ＝角ＯＣＢ＝８４÷２＝４２°です。さらに、角ＯＣＡ＝角ＯＡＣ＝４２°なので角ＡＯＣ＝１８０－４２×２＝９６°となり、同様に角ＢＯＣも９６°となるので９６×２＝１９２°と求まります。
答え：１９２°
(2) 毎回のPとQの重なり方について、各々の点の動き方も踏まえながら、規則がないか調べてみます。１回目…P：時計回り Q：反時計回り　⇒出会い　２回目…P：時計回り Q：時計回り　⇒追いこし　３回目…P：時計回り Q：反時計回り　⇒出会い　４回目…P：時計回り Q：時計回り　⇒追いこし　……といった形で、２回ごとを１周期として出会いと追いこしを繰り返すことになります。(1)で、２回目に重なるまでにPはAから１９２°進みました。本問では４回目を問われているので、PがAから出発して１９２×２＝３８４°進んだことになります。これは３８４－３６０＝２４となり、１周と２４°進んだことになるので、２４°と求まります。
答え：２４°
(3) ４回目に重なったのが(2)よりDで、５回目に重なったのが図２のCです。つまり、４～５回目の間でPはDからCまで動いたことになります。(1)より角AOCは９６°、(2)より角AODが２４°なので、角DOCは９６－２４＝７２°となり、これがPの進んだ角度となります。一方、Qは４回目に重なった後は反時計回りに動いてPと出会うので、３６０（PとQが合計で進む１周分の角度）－７２＝２８８°進むことになります。よって、QはPの２８８÷７２＝４倍の速さで動いていることになります。
答え：４倍
(4) これまでで分かったことを踏まえ、PがAから進む角度を整理すると以下のようになります。

点A上で重なる、ということは上記の表の角度が３６０の倍数にならなければいけません。表の赤字の部分は、一の位が０になる箇所です。また、奇数回目・偶数回目ともに１９２°ずつ増えていくことになり、上記の表を奇・偶で分割してみると以下のようになります。

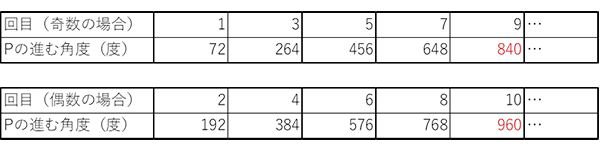
奇数回について見てみると、９回目の８４０°は３６０の倍数になっていません。そこで、８４０＋１９２×□を計算して出た答えの一の位が０になる□を考えると５になり、８４０＋１９２×５＝１８００°、これは９＋２×５＝１９回目のことです。１８００は３６０で割り切れるので、これは条件に適することになります。１９回目の次は、１９２×５＝９６０と３６０の最小公倍数である２８８０°を足すことになり、これは２８８０÷１９２＝１５、１９＋２×１５＝４９回目のことです。以降、３０回ずつ足していくことになるので、問われている２００回目までに１９、４９、７９、１０９、１３９、１６９、１９９の７回が点A上で重なることになります。
続いて、偶数回について見てみると、１０回目の９６０°は３６０の倍数になっていません。そこで、９６０＋１９２×□を計算して出た答えの一の位が０になる□を考えると５になり、９６０＋１９２×５＝１９２０°、これは１０＋２×５＝２０回目のことです。１９２０は３６０で割り切れないので、これは条件に当てはまりません。先ほどの式に戻って計算すると９６０＋１９２×１０＝２８８０°、これは１０＋２×１０＝３０回目のことです。２８８０は３６０で割り切れるので、これは条件に適することになります。　　　　　　　　　　　この次は１９２×５＝９６０と３６０の最小公倍数である２８８０°を足すことになり、これは２８８０÷１９２＝１５、３０＋２×１５＝６０回目のことです。以降、３０回ずつ足していくことになるので、問われている２００回目までに３０、６０、９０、１２０、１５０、１８０（もちろん、３０の倍数と考えても構いません）の６回が点A上で重なることになります。
よって、全部で７＋６＝１３回重なることになります。
答え：１３回

著者：受験Dr. (受験ドクター)

この記事は役にたちましたか？