算数の合否を分けた一題
早実中等部入試対策・算数の合否を分けた一題(2018年度)
難易度分類
| [1] | (1)A(2)A(3)A(4)A |
|---|---|
| [2] | (1)A(2)A(3)B |
| [3] | (1)A(2)①B②B |
| [4] | (1)A(2)A(3)B |
| [5] | (1)A(2)B(3)C |
A:早稲田実業中等部合格を目指すなら必ず得点したい問題
B:着眼点や解法ツールにより正答率・かかる時間に差がつく問題
C:難易度や処理量から判断して一旦とばした方が良い問題
総評
今年度の問題も、例年通り大問が5つあり60分で100点満点の構成になっています。難易度も例年通りで、標準~やや難レベルの問題がほとんどです。まずは標準レベルの問題で確実に得点することが必須になります。平面図形と立体図形の問題は必ず出題されているので、基礎から応用まで幅広く問題演習を行いましょう。また、場合の数や規則性の問題も頻出なので、いろいろなパターンに慣れていきましょう。
問題別寸評
(1)
逆算の問題です。 答 30
小数を分数に変えて計算しましょう。
(2)
(3)
(4)
場合の数の問題です。 答 2通り
1から19までの連続した10個の奇数の和は、1+3+5+・・・+19=(1+19)×10÷2=100になります。つまり、選んだ8個の数と残りの2個の数の和が100、差が40になります。このような2個の数の和は(100-40)÷2=30となります。したがって、和が30になる組み合わせは(11,19)、(13,17)の2通りになります。
(1)
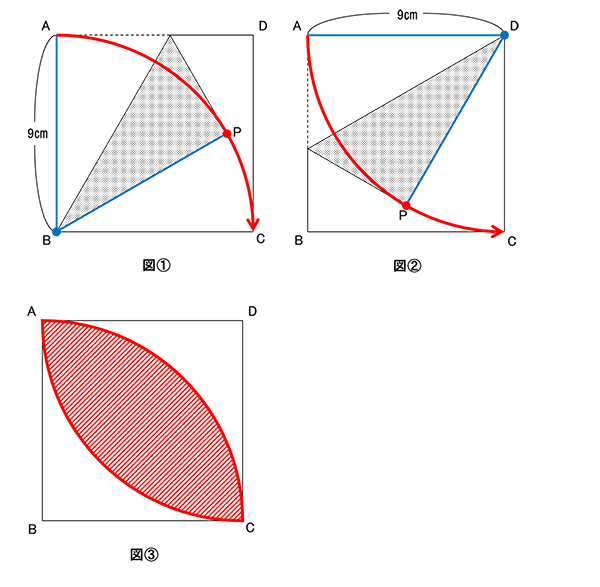
面積から長さを求める問題です。 答 9㎝
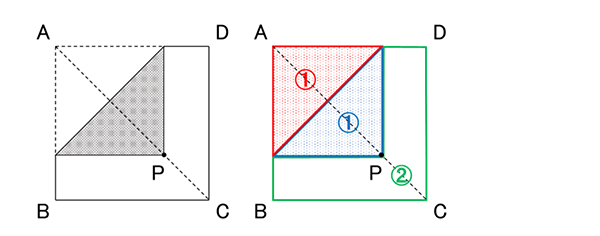
折り返された黒の部分と、折り返される前の部分は合同になるので、面積は等しくなります。黒の部分と白の部分の面積の比が1:2になるので、下の図のように面積の比が1:1:2になるように分けることができます。折り返された部分と折り返される前の部分を合わせると小さい正方形になり、小さい正方形と白い部分の面積の比は2:2=1:1になります。つまり、小さい正方形の面積は、正方形ABCDの半分の9×9÷2=81/2㎠になります。小さい正方形の面積を、対角線APを使って表すと(AP)×(AP)÷2=9×9÷2となるので、AP=9㎝だとわかります。
(2)
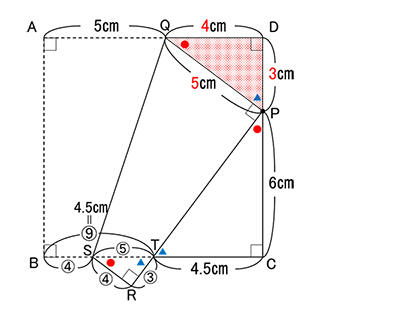
台形の面積を求める問題です。 答 31.5㎠
直角三角形の相似を利用します。三角形PDQ、三角形TCP、三角形TRSは相似形になり、辺の比は3:4:5になります。下の図のように、BTの長さは4:5に分けることができるので、⑨=4.5㎝になり④=4.5÷9×4=2㎝となります。つまり、RS=2㎝になりPR=9㎝なので、求めたい台形の面積は、(2+5)×9÷2=31.5㎠になります。
(3)
作図の問題です。 答 図③を参照のこと
図①のように、点Bを固定しながら点Pを動かすと、必ず黒い図形が三角形になります。点Pの範囲は赤い部分の半径9㎝の四分円までとなります。同様に、点Dを固定しながら点Pを動かすと、図②のようになります。この2つの範囲を組み合わせた図③が答えになります。
(1)
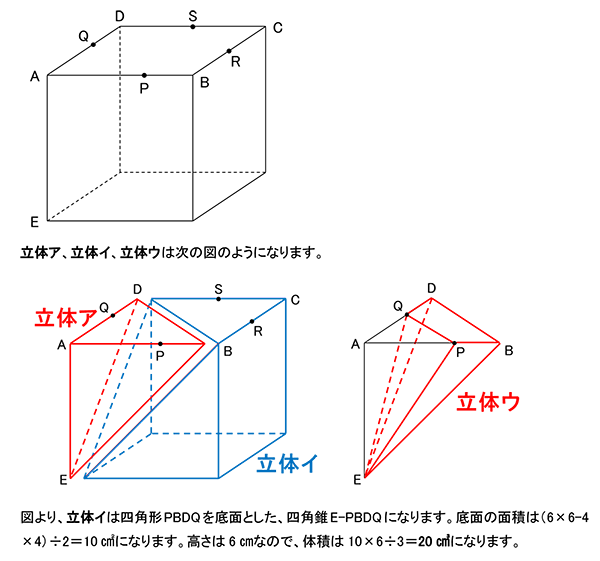
四角錐(すい)の体積を求める問題です。 答 20㎤
(2)
①面積の和を求める問題です。 答 31.5㎠
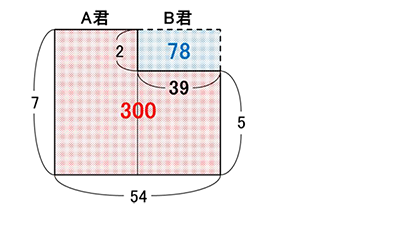
赤色に塗られた部分は下の図のようになります。立方体の辺を延長して、点Fと点Gを作ります。三角形の相似を利用して、BH=DI=2㎝、BF=DG=3㎝になることに着目しましょう。
三角形BEH=三角形DEI=2×6÷2=6㎠
三角形BHR=三角形DIS=2×3÷2=3㎠
三角形BCDと三角形RCSの相似を利用して、
四角形BRSD=3×3÷2×3=13.5㎠
したがって、赤色に塗られた部分の面積は6×2+3×2+13.5=31.5㎠になります。
②立体の体積を求める問題です。 答 39㎤
四角錐E-BFGDから三角錐H-BFRと三角錐I-DGSを引いて求めます。
四角錐E-BFGD=(13.5+3×3÷2×2)×6÷3=45㎤
三角錐H-BFR=三角錐I-DGS=3×3÷2×2÷3㎤
したがって、立方体エの体積は45-3×2=39㎤になります。

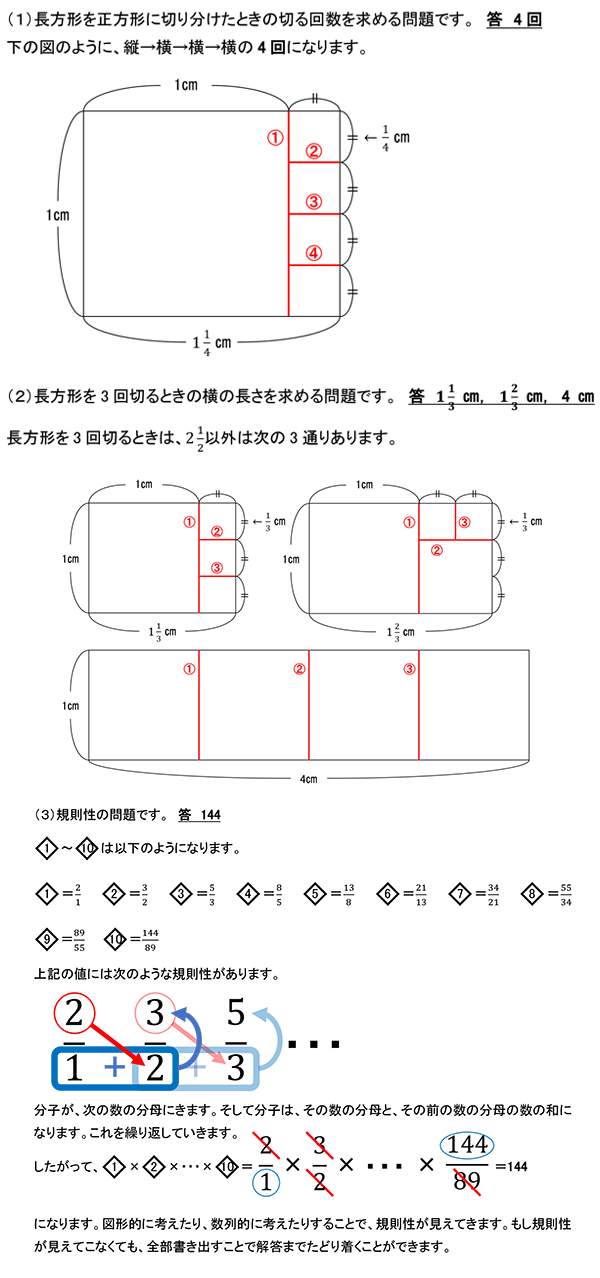
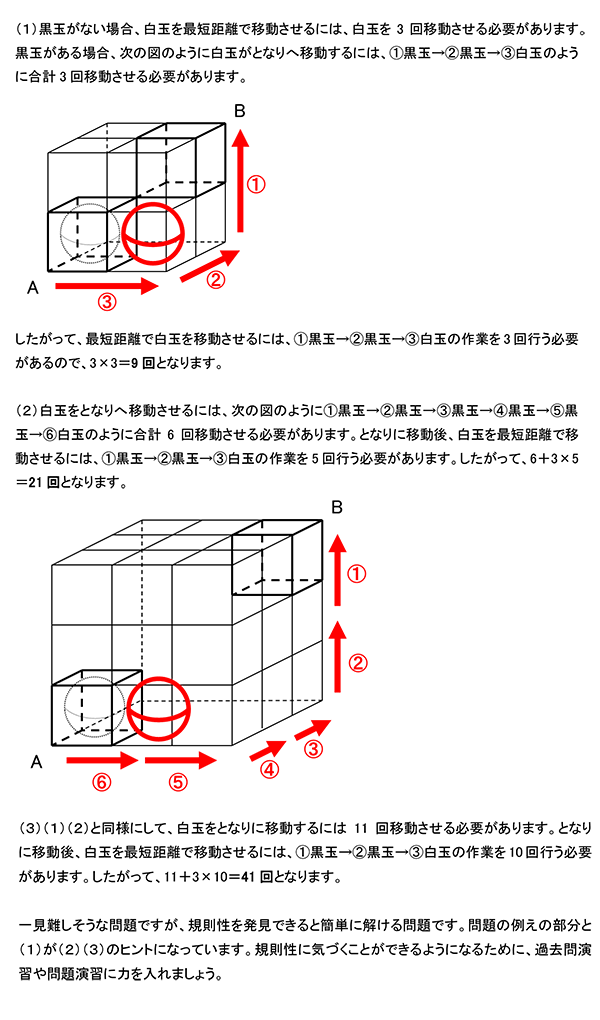
立体図形の規則性の問題です。 答 (1)9回 (2)21回 (3)41回
詳細は合否を分けた一題として後述します。