算数の合否を分けた一題（2015年度）

算数の合否を分けた一題

早実中等部入試対策・算数の合否を分けた一題（2015年度）

難易度分類

大問１	（1）Ａ　　（2）Ａ　　（3）Ａ　　（4）Ａ　(5)Ａ
大問２	（1）Ａ　　（2）①B　②C
大問３	（1）Ａ　　（2）Ｂ　　(3)B
大問４	（1）Ａ　　（2）Ａ　　（3）B
大問５	（1）A　　（2）①B　②B　③C

Ａ：雙葉中学を目指すなら落とすことの出来ない問題
Ｂ：着眼点や解法ツールにより正答率・かかる時間に差がつく問題
Ｃ：難易度や処理量から判断して５分以内に解き切る腕力がなければ後に回すべき問題

問題別寸評

［１］

(１)分数計算です。確実に得点しましょう。

(２)2種類の比が登場するので、線分図を書いて整理⇒式をたて消去残でOKです。

(３)塩の量に注目すると、容器A12g、B36gがA24g、B24gに変化しています。
容器BのがBに入れた水の量です。

(４)平行四辺形を縦に区切る線が、1：1で切断ことがポイントですね。
ア、イ、ウ、エは全て高さの等しい台形です。上底＋下底で面積比を求めましょう。

(５)三角形、四角形の内角の和から追いかけていくだけで求まります。正五角形の１つの内角は108度はもちろん暗記していますね？

［２］図形の移動と条件整理

(１)円すいの半径と母線の比から、展開図の中心角が全体に占める割合がより、二度重なるのは円のつとなります。

(２)この条件整理は曲者です。４つの範囲の重なりなので、線分図で順に絞り込んでゆく必要があります。①は比較的スムーズですが、②は分析に時間がかかりすぎるので、この手の問題がよほど得意でない限り、飛ばす判断が正解です。

［３］平面図形

場合の数と絡んだ良問です。合否を分けた一題として後述します。

［４］速さ

内容としては簡単ですが、文章が長く、条件の数が多いので、混乱してしまった受験生から脱落してゆきます。あわてず丁寧に時間ごとに誰がどこにいるのか調べてゆけましょう。数値も複雑ではありません。
(１)和差算を使って縦と横を求めます。マラソンコースが長方形の道２周分であることに注意。

(２)三郎と次郎が同じ速さで移動している間、つまり次郎がＧについてから次郎がゴールするまでの時間に揃えるのがポイント。

(３)(２)まで出来たのなら、解ききりたい問題です。出来事の順に時間を求めれば終了。

［５］立方体の構成

早実らしい良問です。難易度はかなり高めですが、(１)からはじまる枝問が誘導になっていますので、前の問題を利用しながら解き進めれば(２)②までは得点可能です。

(１)立方体Ｔのなかで最も外に露出する回数の多い「頂点」と「辺」にあたる32個は0が書かれたブロックを使用。残りは24個は、極力１がかかれたブロックを優先し、１のブロック16個、2のブロック8個となります。外に出ている数字の和は32となります。

(２)
①和を36にするとあります。(１)で最も少ない場合32になることから、(１)の状態を少し変化させ和を36にすることを考えましょう。頂点Ａにある2のブロックと、もともと頂点Ａにあった0のブロックの位置を入れ替えると、和は4増え、丁度36になる事がわかります。

②(１)の状態から２のブロックと０のブロックの位置を1組入れ替えれば和が36であることより、今回は点Ｅの２のブロックと、面ＡＢＣＤ上の０のブロックが入れ変わったことがわかります。
どの面も和が６になるには中央４枚が全て１のブロックになればＯＫ。

③捨て問と判断するのが正解でしょう。
(１)の状態から１のブロックを頂点の位置に移動すると、面の和は２増え34となります。
あと２をどのように増やせば良いかに絞って考えましょう。
Ｙに含まれる１のブロックをＸの「辺の位置」に２つ持ってくれば、和が36となります。

合否を分けた一題

今年度も早実らしい良問でしたが、平面、立体図形、速さどれをとっても「比」を使う必要がなく、細かい「条件を考えさせる」問題構成でした。一般的な受験算数では太刀打ちできない、難易度の高い構成です。細かい条件を追っていく問題は、時間がかかり、ミスが生じやすくなります。
分析力、処理力が問われただけでなく、どの問題に時間をかけ、どの問題を捨てるかといった「判断力」が要求されます。
特に序盤の［２］(２)で時間を費やしてしまった受験生は多かったのではないでしょうか。
さて、合否を分けた一題として［３］の平面図形を解説します。
比も登場せず、面積を考えるだけではありますが、誘導にしたがってミスなく状況を分析できるかどうかで合否が別れたでしょう。

［３］平面図形

４つの三角形の面積の条件を踏まえつつ、点Ｐを長方形ＡＢＣＤの内部や外部におく問題です。
（１）ここで問題の設定の意味を理解しておきましょう。ＡＤＰの面積が６であることはすぐに気づきますね。

(２)長方形の内部に点を置き、４つの三角形の面積を考える問題は、多くの受験生が経験したことがあるでしょう。大切なのは「向かい合う三角形の面積の和が長方形の面積の半分である」という基礎知識を知っていたかどうか。
本問は長方形の面積が32㎠ですので、向かい合う三角形の面積の和は16㎠となります。
よって8㎠となる三角形と向かいあう三角形の面積も8㎠であることが解ります。
6㎠の三角形と向かい合うのは10㎠の三角形です。
そのようなペアの作り方は、ＰＡＢとＰＣＤが8㎠の場合に2通り。
ＰＢＣとＰＡＤが8㎠の場合に2通り。
合計4通りとなります。

(３)(１)と(２)を組み合わせて８個、と早とちりしないよう注意。
早実の問題がそんなに簡単なわけがないと、疑いつつ分析しましょう。
(２)の「向かい合う三角形の面積の和が長方形の面積の半分である」が有効なのは点Pが長方形の内部にあるときのみです。外側にあるときは、6㎠、8㎠が1つずつしか存在しない場合もあります。そこで、等積変形を利用し、三角形が6㎠、8㎠となる点Pのラインをイメージして解きます。
例えば三角形PADの面積が6㎠となるのは点Pが辺ADから1.5cm離れた直線上にあるときです。また、三角形PABの面積が8㎠となるのは、点Pが辺ABから4cm離れた直線上にあるときです。つまり図の点線が交わる位置に置いて、三角形PADが6㎠、PABが8㎠となります。
これを内側、外側及び、三角形PBCが6㎠、PCDが8㎠も含めて作図を行うと、下図の右のようになり、点Pは１２個。

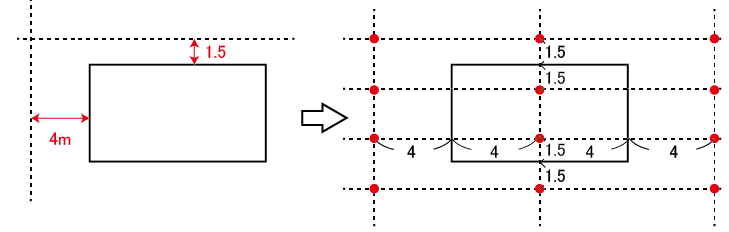
同様に、三角形PADが8㎠、PABが6㎠になる場合、三角形PBCが8㎠、PCDが6㎠になる場合の作図を行うと、点Pは12個。

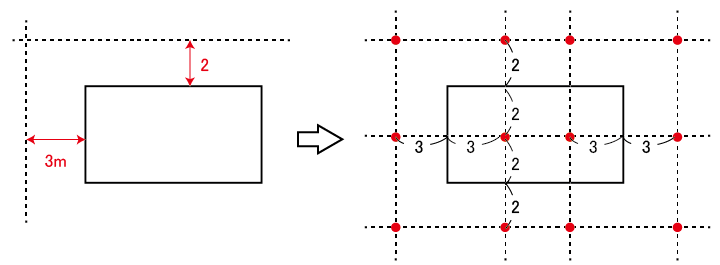
合計12＋12=24個と求まります。