算数の合否を分けた一題（2019年度）

算数の合否を分けた一題

早大学院入試対策・算数の合否を分けた一題（2019年度）

難易度分類

１	（１） ① A　　 ② A　　（２） ① A　　② C
２	（１） A　　（２） A　　（３） B　　（４） B
３	（１） A　　（２） A
４	（１） A　　（２） C　　（３） B

A…早大学院合格を目指すなら、確実に得点したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難易度、処理量から判断して、得点差がつかない問題

出題総評

例年通り大問４つからなる出題でした。
問題数が少なく、出題傾向の読みづらい学校ですが、毎年平面図形の問題が難問となっています。
大問１は計算と平面図形、大問2は立体図形、大問３は不定方程式、大問４は平面図形の規則性でした。
出題が図形に偏った年度だったので、図形問題の発想力が大きく点差を分けたと思われます。

問題別寸評

１計算・平面図形

（１）の計算問題は例年よりも処理しやすくなっていますが、（２）②は難問と言っていいレベルでした。前半部分にまぎれこんでいる難問に悩みすぎて時間配分をミスしないよう気をつけましょう。大問1の時間配分の目安は10分以内です。悩む前に次の大問に目を通しましょう。
平面図形の練習のために早稲田中の2018年大問２なども解いておくと良いでしょう。

（１）①

そのまま通分して足していくと分母が大きくなりすぎるので、足しやすい数（分母が2の倍数、3の倍数のもの）どうしを先に足して約分しましょう。2013年の過去問なども参考になります。

（１）②

単純な逆算です。必ず得点しましょう。

（２）①

高さの等しい三角形なので、△ABD：△DBC＝AD：DCです。△ABCは直角二等辺三角形なので、1辺の長さがわかれば面積は求められます。

（２）②

　　　→ 合否を分けた一題参照

２立体図形

立体図形上の最短距離を求める問題です。立体図形の出題頻度はそれほど高くないですが、立体切断や最短距離の問題などの面に注目して解く問題が出題されています。1つの面を抜き出して描き、その中を平面図形の問題として処理する流れに慣れましょう。

（１）①

三角形の相似から、辺の中点にきたときにAD（BC）の半分の長さの正方形ができます。
なんとなく形はイメージできてしまいますが、根拠を言えるようにしておきましょう。　

（１）②

言い回しにだまされないよう注意です。BQ＝27cm ⇒ DQ＝36－27＝９cmということなので、
DQ＝DRとなりQRはBCと平行とわかります。

（２）～（４）

最短距離の問題なので、展開図を描いて解きます。点と辺を最短で結ぶには、辺に垂直な補助線を引きます。問題文から何面分の展開図が必要なのか読み取って図を描き、相似を見つけましょう。

３不定方程式

「式や考え方を書いて説明」する問題は2問出題されることが多いですが、2019年はこの1問のみでした。2種の不定方程式なのでそれほど時間をかけずに調べられると思います。詳しく書こうとして時間をかけすぎてしまうことや、途中式を省略して減点されてしまうことに注意しましょう。

（１）

調べる回数を減らすために、1個あたりの使用材料が多い商品を基準にしましょう。「Bを20個つくると～」くらいの文章は書いておきましょう。

（２）

（１）が解けた人へのサービス問題です。値段の高いBが最多の場合を考えます。

４図形の規則性

いわゆる約束算の問題は毎年出題されています。今年に関しては図形問題との複合になっているので、頭で考えるだけでなく自分で図を描いてイメージすることが重要です。
また、操作回数がまぎらわしくなっています。はじめの操作は1回目ではなく☆、何回できるかではなく何回目でできなくなるかを答えます。過去問を解いていく中で約束の部分を勘違いして失点した経験のある人は、リード文をしっかり読み、ポイント部分に線を引いて確認しましょう。
武蔵中や麻布中などの少し難しい約束算の問題にチャレンジして慣れておくと良いです。

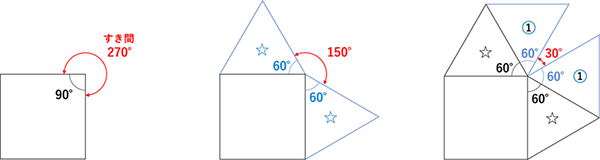
（１）

360°から内角を引いたすき間の角（図形の外側にできる角）を考えます。
正方形だとすき間は270°残っていますから、
ここから☆の状態にすると正三角形2つ分減るので270－60×2＝150°
1回目の操作をすると150－60×２＝30°
次の2回目の操作で正三角形が入りきらなくなるので答えは2回です。

（２）

（１）と同様に内角の反対側のすき間に注目します。
操作が3回できるということは、2回までは重ならないということなので、☆の状態と併せて底角30°の二等辺三角形が最低3組入ることになります。すき間は少なくとも（30°×2）×3組＝180°以上。最大値は4組が重ならずにぴったり入るときなので、（30°×2）×4組＝240°以下となります。
内角は360°からすき間の角度を引いたものなので、120°以上180°以下となります。辺の数が最も少ないのは内角が最小値120°の正六角形のときです。

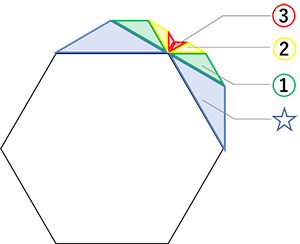
上図は操作が3回ちょうどで終わった場合の図です。
このとき内角が最小になることをイメージできてい
ればすぐに答えにたどりつけます。

（３）

すき間の角が270°です。☆も含めて45°の直角二等辺三角形が270÷（45×2）＝3組入ります。
下図より、☆の三角形が4個、操作①の三角形が8個、操作②の三角形が16個できます。

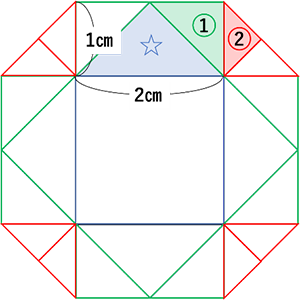
☆は2cm×1cm÷2×4個＝4㎠
①は☆の半分の面積なので、①×8個は☆×4個と同じく4㎠
②は①の半分の面積なので、②×16個は①×8個と同じく4㎠
面積の和は4㎠×3＝12㎠となります。
（２）と違って実際に図を描いてイメージできる問題なので、
（２）をとばして先に解くという判断でも良いでしょう。

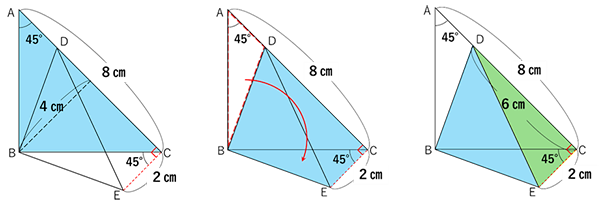
合否を分けた１題

2019年入試のポイントは何と言っても平面図形です。例年であれば速さや割合の少しひねった問題を織り交ぜてくるのですが、今年は平面図形で直球勝負にきた印象です。
大問４も問題文をしっかり読み取れていないと（２）（３）と連続失点してしまう危険性があります。中でも、2019年入試の合否を分けた一題は、大問１（２）②だと言えます。
この問題は早大学院や他の早稲田系列の出題傾向からすると珍しいというわけではないのですが、通常の算数対策ではあまり出くわさないパターンです。大問１という序盤で悩んでしまい時間配分で大失敗する可能性があります。もちろん解法パターンの対策をしっかり立てておくことが重要ですが、いったんあきらめて次の問題に移るという判断も有効な、合否を分けた一題でした。

（２）②

同じ形の三角形を2枚重ねると合同な三角形ができます。気づくことができれば解き進められますが、普段は三角形の相似ばかり探す癖がついてしまっているのでなかなか発見できません。他の学校ではあまり使わない発想なので、早大学院の過去問を解く際は常に合同になることを疑って解いてください。

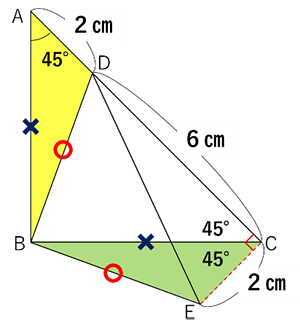
二等辺三角形が出てきたら等しい長さ・角度に必ず書きこみをしましょう。
合同な三角形が見つかったら、長さ、角度、もちろん面積も等しいので、
すべて図に書きこんでから解き方を考えてください。