理科の合否を分けた一題（2019年度）

理科の合否を分けた一題

早大学院入試対策・理科の合否を分けた一題（2019年度）

難易度分類

１	問１ A　　問２ A　　問３ A　　問４ B　　問５ A　　問６ B　　問７ A問８ A　　問９ A　　問10 A
２	問１ A　　問２　A　　問３ A　　問４ A　　問５ A　　問６ A　　問７ A問８ B　　問９ B　　問10 B　　問11 B
３	問１ A　　問２ A　　問３ B　　問４ A　　問５ A　　問６ B　　問７ B
４	問１ A　　問２ A　　問３ A　　問４ B　　問５ B　　問６ B　　問７ C問８ B

A…早大学院合格を目指すなら、確実に得点したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難易度、処理量から判断して、部分点を拾えればよしとする問題

出題総評

2019年度の早大学院は、例年通り、幅広い知識と、根本原理の理解を問う問題が中心です。
全体に計算力が求められる問題が多く、難易度は昨年度とくらべてかなり上がっています。
例年、１分野に２つの題材が取り上げられることが多いのですが、本年は各分野１題材で、じっくり深く掘り下げた出題構成になっています。

生物分野の問題は、植物の種子と発芽についての問題。
化学分野の問題は、食塩の濃度と結晶の取り出し方についての問題。
地学分野の問題は、地層のでき方についての問題。
物理分野の問題は、浮力についての問題。

理科的な思考と、原理原則に基づいた処理が必要な問題が中心です。
対策としては、どの分野もまんべんなく学習し、弱点を残さないこと。根本原理をおさえた上で、知識をきちんと整理して、使えるものにしておくことが大切です。
１と２のオーソドックスな問題で確実に得点したうえで、２以降の思考力、計算力をどれだけ発揮できるかが合否を分けるといえます。

問題構成は、４分野から大問4題、小問43問。
解答形式は、記号選択が29問、言語が５問、数字が３問、記述が３問、作図２問、グラフが１問。
選択肢は、昨年に比べて大幅に増え、難易度にメリハリがあります。計算が必要なものが多く含まれています。
言語は昨年と比べて減少し、基本の知識ばかりでした。
数字で答える問題は、濃度と浮力の問題で出され、かなりのボリュームがあり、時間内に処理するための工夫と計算力が求められます。
記述は、10字以内、１行程度、25字以内と制限があり、導入にそって考えをまとめ、文字に落とす形のものでした。
作図は、インゲンマメの果実とろ過のようすを書くものでした。
グラフは、数的処理をした数字を反映させるものでした。
試験時間は40分ですから、最後まで気を抜かずに解き切ることが大切です。

問題別寸評

１

（生物）植物の種子と発芽についての問題です。
オーソドックスな知識の問題です。どれも基本の知識ばかりですから、ミスせず確実に解答することを目指します。

問１

種子の図は、左から順にインゲンマメ、カキ、トウモロコシです。カキは有胚乳種子ですから、子葉は小さな葉の形をしているカです。

問２

インゲンマメは無胚乳種子なので、アの幼芽、イの胚じく、ウの子葉のすべてが、発芽した時に体になる胚にあたります。

問３

有胚乳種子であるカキのキ、トウモロコシのケが、それぞれ胚乳にあたります。

問４

アのマツは風媒花で、空気の入ったふくろを持っています。エのトウモロコシも風媒花のなかまで、とても小さくでっぱりのない丸い形です。イのヘチマは虫媒花でまわりにとげがあり、虫の体にひっかかるようになっています。ウのカボチャも虫媒花でとげはありませんが、めしべの柱頭にねばりけがあり、つきやすくなっています。

問５

カキやミカンは子房が変化したおいしい果実をもち、動物がこれを食べフンと一緒に種子を出すことで、遠く離れた場所に運ばれます。
タンポポ、マツ、カエデの種子は風で運ばれ、オナモミは動物の体にくっついて運ばれます。

問６

インゲンマメの果実は、種子が入っているさやの部分です。全体に細長く種子のあるところがふくらんでいる形です。

問７・８

実験の条件をまとめると、下の表のようになります。発芽の３条件のうち、比較ができているのは、空気と水です。実験３で発芽していることから、適当な温度の条件は満たしていると考えます。

	空気	水	適当な温度
実験１	〇	×	〇
実験２	×	〇	〇
実験３	〇	〇	〇

問９

発芽した実験３の「適当な温度」の条件を満たさない方法を考えます。
選択肢があり、比較的選びやすい内容です。

問10

成長の５条件は、発芽の３条件に、光、肥料の２つの条件を加えたものです。
これも、基本の知識です。

２

（化学）食塩の濃度と結晶の取り出し方に関する問題です。
前半はごく基本の知識の問題ですが、後半は溶解度のグラフの数値を使って計算する問題です。解答は選択肢になっているので、計算に時間がかかり過ぎないように、工夫して処理することができた方が有利といえます。

問１

ろ過のようすの図を完成させる問題です。必要な器具が示されていて、対応しやすくなっています。
よく出題される図なので、書けるようにしておきたい問題です。

問２

実験器具のなまえも頻出です。しっかり確認しておくことが大切です。

問３

物質によって結晶の形に特徴があるものについて、代表的なものはおぼえておきましょう。食塩の結晶は、立方体の形です。

問４

ろ過は、液体と固体の混合物から、固体を分離する方法です。取り出すことができる固体は、ろ紙の目の大きさより大きいことが条件になります。

問５

食塩水は電気を通す水溶液です。電気を通す水溶液は、酸性の炭酸水とアルカリ性の石灰水・水酸化ナトリウム水溶液の３つです。中性の砂糖水とアルコール水溶液は電気を通しません。
これも、基本の知識です。

問６

溶質が固体の水溶液は、石灰水・砂糖水・水酸化ナトリウム水溶液です。炭酸水は気体、アルコール水溶液は液体がとけている水溶液です。

問７

飽和水溶液は、温度が同じなら量の多少にかかわらず濃度は同じです。
グラフから、20℃のとき100gの水に溶かすことができる食塩の量は約37.8ｇなので、このときの濃度は、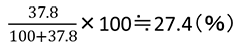です。

問８

28％の食塩水の水と食塩の量の比は、72：28です。これを水100ｇに換算すると、28×100/72≒38.9（ｇ）の食塩が溶けていることになります。グラフの値にあてはめると、55℃前後で飽和するとわかります。

問９

問10

問11

食塩の溶解度は、温度による変化が少ないという特徴があります。
問９で温度を下げただけの場合はわずか６ｇの食塩しか得られませんでしたが、問10で水を蒸発させた場合は120ｇと多くの食塩を取り出すことができます。実際に塩田では、海水の水分を蒸発させる方法で塩を取り出しています。

３

（地学）地層のでき方についての問題。
地層や岩石に関する問題では、火成岩や化石の知識がしっかり身についていることが前提となっているので、しっかり整理しておきましょう。

問１

Pを境に、上の地層と下の地層のたい積の様子がちがいます。これは、地層A～Eが堆積した後、隆起して地上になり、侵食されてできた面だからです。このあと再び沈降して海底になり、地層Gが堆積したと考えられます。このような面Pを、不整合（面）といいます。

問２

まず、粒が角張っていて結晶が大きく成長していることから、深成岩とわかります。また、有色鉱物の割合より無色鉱物の割合が多く、有色鉱物としてクロウンモを含んでいることから、カコウ岩と判断します。岩石の知識は時折詳しめに聞かれることがあるので、きちんと知識を整理しておくことが大切です。

問３

地層Fが火成岩であることから、できた当時は高温のマグマであったと考えられます。堆積岩が高温のマグマに接して、性質が変化したものが変成岩です。

問４

地層Cは地層Bより新しく、地層Dより古い層です。
示準化石であるサンヨウチュウが見つかった地層Bは古生代、アンモナイトが見つかった地層Dは中生代の地層です。フズリナは古生代、キョウリュウは中生代、マンモスは新生代の化石なので、可能性がないのはマンモスです。

問５

断層Rは逆断層で押されてできたとわかります。断層Sは正断層で引っ張る力がはたらいたと考えられます。

問６

つくられた順に、A→B→C→D→E→F→R→P→G→Sとなります。
断層Rは不整合面で切れていて、不整合面は断層Sで切れていることが手掛かりとなります。

問７

露頭Xと露頭Yを手がかりに、底面Zに見られる地層を書き入れると、下の図のようになります。
あとうは地層C、いは地層CとDの境目にあたります。

４

（物理）浮力に関する問題。
金属板から箱舟をつくり、これを水に浮かせます。
金属板の総面積が決められているので、この条件のなかで計算力と思考力をはたらかせます。

問１

底が一辺６cmの正方形なので、壁の高さは（150-6×6×2）÷（6×4）＝3.25（cm）とわかります。

問２

２cm沈んだときの浮力は、6×6×2×１＝72（ｇ）です。これは、箱舟Aと砂のおもさとつり合っているので、金属板の重さは72-45＝27（ｇ）

問３

箱舟Aがすべて水中に沈んだときの浮力は、6×6×3.25×1＝117（ｇ）なので、砂は最大90ｇ（117-27）まで入れることができます。

問４

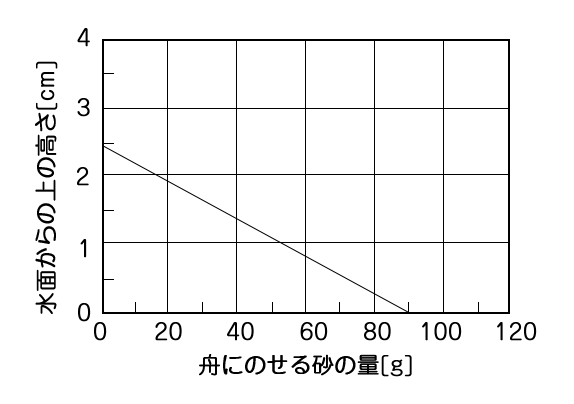
砂の量が０ｇのとき、Aは0.75cm（27÷（6×6））沈み、このとき水面から上に出ている高さは2.5cm（3.25-0.75）です。砂が45ｇのときの数値とともにグラフに書き入れると、図のように直線のグラフになり、ちょうど90ｇですべて水中に沈むことがわかります。

問５

水深が１cmの水そうには、水面から１cmしか沈むことができないと考えます。
底面積は、Bは49cm2（7×7）、Cは36cm2（4×9）、Dは48cm2（4×4×3）なので、1cm以内で47ｇ（27＋20）の浮力を得ることができるのは、BとDです。

問６

→合否を分けた一題参照。

問７

砂の最大量は舟の体積で決まります。また、底面は周の長さが短い正方形に近い方が、高さを大きくとれるので、全体の体積を大きくすることができます。

問８

同じ表面積のとき、球が最も体積が大きくなり、浮力も大きくなります。
そのまま書けばよい問題です。

合否を分けた１題

適当なグラフを選択肢から選ぶ問題です。ポイントをしぼって、すばやく判断することが大切です。
ここでは、最大になる位置と量、加えてもう１点を確認することで選ぶことができます。
思考力と計算力、すばやい判断をフルに活かせたかどうかが、合否を分けたと考えられます。

４

問６

表面積が一定のとき、体積が最も大きくなる形は球です。球に最も近い形は立方体です。まず、このアプローチから出発できると有利です。
この金属板からは、150÷６＝25（cm2）より、一辺５cmの立方体を作ることができます。このとき、砂の最大量は、5×5×5×1－27＝98（ｇ）。これで、グラフのピークが決まります。
さらに、底の一辺が２cmのときについて計算します。このときの高さは（150―2×2×2）÷（2×4）＝17.75（cm）で、砂の最大量は、2×2×17.75×１－27＝44（ｇ）。
以上から、エが適当とわかります。

著者：S.O.

この記事は役にたちましたか？