算数の合否を分けた一題（2018年度）

算数の合否を分けた一題

早大学院入試対策・算数の合否を分けた一題（2018年度）

難易度分類

［１］	(1)A　(2)A　(3)①A ②A
［２］	(1)B　(2)B　(3)B
［３］	(1)B　(2)B　(3)C
［４］	(1)A　(2)A　(3)A　(4)C

Ａ：早大学院合格を目指すなら必ず得点したい問題
Ｂ：着眼点や解法ツールにより正答率・かかる時間に差がつく問題
Ｃ：難易度や処理量から判断してとばすべき問題

出題総評

今年も、大問１は計算を含む小問集合が全４問、大問２～４は様々な単元にわかれた昨今の形式が踏襲された入試となりました。
詳細については、大問１が分数や小数の混合計算および場合の数、大問２は速さ、大問３は平面図形、大問４は数の操作の問題でした。

問題別寸評

［１］

(1)

答　９３６０
分数と小数が入り混じった計算問題。２３４×…の部分は工夫をするように。落ち着いて計算していきましょう。

(2)

答　あ…１　い…３　う…０　え…１　お…４
空欄に数を補充して式を計算することで、特定の数を作らせる数の性質の問題。まず、２０１８÷１０＝２０１．８となり、０．８をどう作るかに着目します。あ、い、う、えに整数を入れただけでは作れないので、お÷５で０．８を作ったことになる。ここから、まずは　お…４　となります。続いて、残りの式は　あ×１２５＋い×２５＋う×５＋え＝２０１　となり、一の位に着目すると　え…１　が決まります。残りの２００が成立するように　あ、い、う　を定めていきます。

(3)

答　①６０個　②４通り
カード並べをテーマにした、数の性質と場合の数の問題。
作る数が９の倍数なので、各位の和も９の倍数になります。和が９…（１，２，６）（１，３，５）（２，３，４）　和が１８…（１，８，９）（２，７，９）（３，６，９）（３，７，８）（４，５，９）（４，６，８）（５，６，７）　どの組も０を含まないので、それぞれ並び替えて６個ずつの数が作れます。
十の位と一の位をひっくり返した時に、偶数になってしまうので元の数の十の位が偶数であることはありえません。同じ理由で、５で割れてしまうことからも元の数の十の位は５ではありません。このことから、元の数の十の位は１，３，７，９と絞れます。その上で素数を探していくと、１３・１７・３７・７９となります。

全ての問題において、ここでの失点は避けたいところです。

［２］

答　（１）１５００m　（２）２７分後　（３）２５０m
２人が登場する旅人算の問題。太郎、次郎ともに何度もＡＢ間を往復するので、線分図よりダイヤグラムのほうが、描く手間があるとはいえ本問の攻略には適しているでしょう。
太郎の休みの時間は６０秒＝１分、次郎の休みの時間は９０秒＝１．５分としてダイヤグラムを描くと以下のようになります。

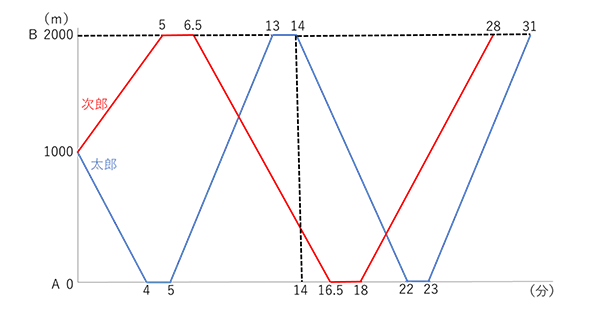
（１）

太郎がはじめてＢを出発する１４分後に着目します。次郎が、あと１６．５－１４＝２．５分でＡにたどり着くので、その距離を計算したあとに全体の距離から引けば答えが求まります。

（２）

１４分後に、二人は（１）の答えより１５００m離れていることが分かりました。しかし、その２．５分後に次郎がＡに着きます。２人の間は、（２５０－２００）×２．５＝１２５mしか縮まないので求めるべきはＡからＢに向かう時（次郎なら１８分後以降、太郎なら２３分以降）ということになります。太郎が出発する２３分後の時点で、二人は２００×（２３－１８）＝１０００m離れており、その差が８００mになればよいのであと（１０００－８００）÷（２５０－２００）＝４分かかることになります。これはまだ、次郎がＢに到着していないので成立します。

（３）

太郎がＢを出発するのが１４分後で、出発地点（＝ＡＢの中間地点）を通るのは１４＋１０００÷２５０＝１８分後です。次郎は休み終わり、Ａを出発した瞬間です。その時の二人の情況、そして二人が同時にＢに到着するまでの様子を線分図にすると以下のようになります。

太郎は、図の青色の点線の部分を１０００÷２５０＝４分で進むので、出発してから向きを変えるまでの時間が（１０－４）÷２＝３分ということになり、ここから距離を求めれば答えが求まります。

［３］

答　（１）７８０cm　（２）１３００cm　（３）１６２５０㎠
詳細は合否を分けた一題として後述します。

［４］

答　（１）あ…１１　い…１９　（２）う…１　（３）え…５　（４）お…４１
数が、偶数であるか奇数であるかによって操作の内容が異なる、数の操作の問題。例示もあり、ルールがシンプルなので問題全体の難易度は高くはないでしょう。

（１）～（３）

題意が掴み取れているか、の確認問題です。ルールに従って計算すると
２６（偶）→１３（奇）→２２（偶）→１１（奇）→１９となります。
３２＝２×２×２×２×２なので、５回操作をする＝２で５回割ると１です。
２３（奇）→３７（奇）→５８（偶）→２９（奇）→４６（偶）→２３（奇）となります。
最後の大問とはいえ、ここまでの失点は許されません。

（４）

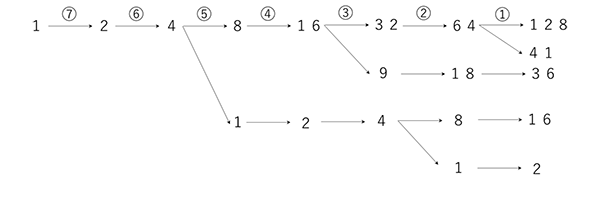
樹形図を使いながら、さかのぼって調べていきます。[１]の計算であれば、その数に２をかける。[２]の計算であれば、その数に２をかけた後、５を引いて３で割ります（ここで５を引けなかったり、３で割り切れない場合は考える必要はありません）。
整理すると、以下のようになります。