算数の合否を分けた一題
早大学院入試対策・算数の合否を分けた一題(2016年度)
難易度分類
| [1] | (1)①A ②B (2)①A ②B |
|---|---|
| [2] | (1)A (2)A |
| [3] | (1)A (2)A (3)B (4)B (5)C (6)C |
| [4] | (1)A (2)A (3)B |
A…早稲田高等学院中合格を目指すなら必ず得点したい問題
B…着眼点や解法により正答率・かかる時間に差がつく問題
C…難易度や処理量から判断して、後回しにしたほうがよい問題
問題別寸評
(1)
①学院特有の「考えさせる」計算問題です。 小数、分数混合の単なる計算ではなく、問題に条件があり、小数の一部の数字を求めさせる問題になっています。なので、一旦まず問題を見たら、「どういう方針で解くべきか」を考えてから手を付けてください。やみくもに計算してしまうと時間だけがかかって正解に辿り着けないということになりかねません。計算問題で「頭を使わせる」問題というのは、まずは工夫することがあげられるでしょう。学院は更に、どうやったら答えにたどり着くのかという道筋を立て、時間も考慮して解き進めなくては行けません。
②こちらも①と同様、一旦計算する前に「どの手順で解くか」を考えてから計算し始める必要があります。分母にある分数の中の分数がやっかいなので、3.14×□□=4という形に持っていって□を求めるようにしましょう。方針もそうですが、数字もかなり厄介です。時間がかかる問題です。しかし、後半部分を考えると、そこまでこの(1)に時間はかけられません。計算2問で10分を目安に解きましょう。
総じて難易度が高く一筋縄ではいかないです。
(2)
①図形の問題です。
昨年の平成27年度も同じような問題がでています。角度を求めさせる問題ですが、図形を切り貼りして同じ辺のところにくっつけて二等辺三角形を作る問題です。正方形の中だけの角度を求めていても答えに辿り着きません。そういう時に何を考えるのか、「同じ辺」に気付いて二等辺三角形を作れたかがポイントになります。角度を求める問題の根本は「二等辺三角形を探す」「正三角形を探す」ために同じ辺には同じマークをつけるということです。これは、弊社の『イメージde暗記「根本原理」ポイント160』に詳しく説明されています。
②面積の問題です。
三角形AEFに点Aから辺EFに垂直な線を引いて、辺EFとの交点をHとします。三角形AHFと三角形ADFが等しくなり、三角形AEHと三角形AEBも等しくなります。三角形ECFが正方形ABCDの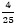 倍なので、五角形ABEFDは
倍なので、五角形ABEFDは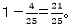 三角形AEF=
三角形AEF= となります。
となります。
なので、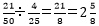 倍です。
倍です。
これはボーナス問題でしょう。ここで時間を稼げていれば後半大問2題に余裕がでてきます。
速さと比の問題ですが、問題で言われていることをしっかりと読みとればそこまで計算も方針も複雑ではありません。
(1)
「はじめに設定していた目標の時間」と「AC間の速さでCB間も進んだ時にかかった時間」と「CB間をAC間の速さの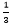 で進んだ時の時間」をそれぞれ比で表しましょう。
で進んだ時の時間」をそれぞれ比で表しましょう。
(2)
「はじめに設定していた目標の時間」から「AC間にかかる時間」を引いたときに求められる時間がCB間にかかった時間になります。
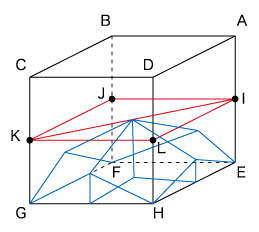
立体切断の問題です。
後半(4)〜(6)は難易度が上がり、切断面がしっかりと描けないと正解に辿り着くのは難しいでしょう。
(1)(2)
切断ルールに則ってしっかりと切断した後の立体や切断面を描けるようにしておきましょう。
(3)
立方体の半分から三角すいを2つ引きます。
三角すいはG−KJLとB−IJLです。
(4)(5)
更に切断されるパターンです。
断頭四角柱が現れます。
(6)
断頭四角柱が4つ分なので、
5×5×5×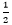 ×4=250㎤
×4=250㎤
合否を分けた一題で詳しく見ていきます。
合否を分けた一題
総評として、今年の本校の問題は、大問4題で問題数は20題(例年15題~20題)。ここ2〜3年落ち着いてきた感じではあります。例年通り、やはり最初の計算問題で時間をかけ過ぎてしまうと後半きつくなるので、始めが侮れないのは変わりません。計算問題、特にただ単純に小数・分数・逆算が出来ればいいということではなく、問題を解く前に何をつかえばいいのかを考えさせる問題になっているので、早稲田高等学院中等部の過去問の計算に特化した練習が必要です。「工夫」や一旦手を止めて頭で考える問題をピックアップして解いていくようにしましょう。大問[2]は、特に計算力も必要なく、速さと比のオーソドックスな問題でした。ここで時間を稼げた生徒も多かったのではないでしょうか。[3]は、立体切断です。斜めに立方体を切ったときの体積を求めさせる問題です。
「目盛りが等間隔ではない物差しが2つあり、その2つの物差しの目盛りのふり方は同じである」ということと、「条件」を理解してから解きましょう。
(1)
題意のまま、4÷2.5=1.6
(2)
同じく題意をしっかりと読み取れば簡単です。
ア×ア=ウより、2×2=4か3×3=9 答え、4か9
(3)
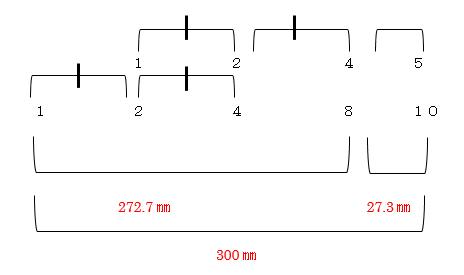
①1,2,4の幅が3区間あるので、272.7㎜÷3=90.9㎜
②1と2の間が、90.9㎜となります。 90.9×2+27.3=209.1㎜


 (3 votes, average: 3.67 out of 5)
(3 votes, average: 3.67 out of 5)