算数の合否を分けた一題（2021年度）

算数の合否を分けた一題

慶應湘南中入試対策・算数の合否を分けた一題（2021年度）

難易度分類

【１】	（１） A　（２） A　（３） A
【２】	（１） A　（２） A　（３） B
【３】	㋐ B　㋑ B　㋒ B
【４】	（１） A　（２） B　（３） B
【５】	（１） B　（２） B　（３） B
【６】	（１） A　（２） B　（３） B

A…慶應湘南藤沢中合格を目指すなら、確実に得点したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難度、処理量から判断して、得点差がつかない問題

2021年度　出題総評

本年度も、近年定着している大問6題の出題。【２】までは計算と小問集合で【３】からが
大問という形式にも変化はありません。

【３】以降では適度に差がつきそうですが、本年は極端な難問や処理量の多すぎるような設問は見当たらず、合格者の間では高得点での勝負になったかもしれません。

例年同様に、【２】までの全問と、【３】以降の大問の前半部分での取りこぼしをせず、残った時間でやや難しい問題を1つでも多く解決するという取り組みが重要となるセットになっています。

2021年度　問題別寸評

【１】計算・小問集合

（１）

本番では、ただやみくもに計算を進めた受験生も一定数いたかもしれません。
分配法則を用いてまとめられる部分をまとめながら計算することで、時間短縮とミス防止を図ることができます。

（２）

逆算タイプの計算問題です。確実に正解しておきたい設問です。

（３）

左下部分の葉っぱの形を2分割して埋めかえることで、半径28cmの四分円から直角二等辺三角形を取りのぞいた図形として求められます。
合格レベルの受験生は、何度も触れている図形でしょう。

【２】　小問集合

（１）

和が一定の倍数算です。比の和をそろえるため、移した後の水の量の比を2倍し、7：3→14：6として考えます。
SFC受験生ならば、基本問題として定着しているはずの問題です。

（２）

与えられた3つの条件を足して2で割ることにより、(137＋118＋129)÷2＝192個がA、B、Cの箱に入っているボールの個数の和であることが分かります。
こちらも大変基本的な出題です。

（３）

「数独」と呼ばれるパズルを題材にしています。経験していた受験生には有利だったでしょう。

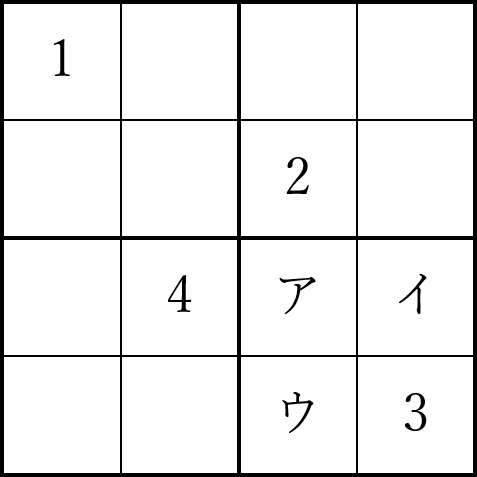
図で、例えばアのマス目に注目すると、条件から2、3、4が入ることはありません。よってアに入る数は1であることが分かります。
アに1を入れると、イには1、3、4が入らないことから2が入り、ウには4が入ることが分かります。

以下同様に、空いているマス目について、そこに入ることのできない数を考えていくと、順に埋めていくことができます。

【３】　立体図形(水量変化とグラフ)

㋐
初めの10秒間、Aの部分にはXが入っているので底面積は4×4－4＝12㎠になっています。
この部分に毎秒8㎤の水が入るので10秒後には8×10＝80㎤の水が入っています。
よって、このときの高さは80㎤÷12㎠＝20/3cmです。

㋑
Xが引き抜かれた状態で水の高さが10cmになるためには、4×4×10＝160㎤の水を入れる必要があります。
よってこのときの時間は、160÷8＝20秒です。

㋒
㋑で求めた20秒から68秒の間の48秒間のうち、Dのふたが開いている間は8－2＝6㎤/秒の割合で、Dのふたが閉じてからは8㎤/秒の割合で容器内の水が増えていきます。
48秒間で容器内に増える水は8×4×10＝320㎤ですから、あとはつるかめ算の考え方を用いて求めることができます。

【４】　数の性質・やりとり算

（１）

与えられた例の通りに作業を進めれば問題なく求めることができます。
( A, B)
はじめ　(40,40)
→１回目　(20,60)
→２回目　(50,30)
→３回目　(25,55)
と推移して、Aさんが25個の玉を持って3回で操作が終わることが分かります。
なお、例で与えられている作業の5倍の玉を常に持っていることに気がつくと、見通しよく求められます。

（２）

作業によって2人の持つ玉の数の和は変化しません。よって2人は合わせて常に63＋129＝192個の球を持っています。したがって、はじめに持っていたのはそれぞれ192÷2＝96個です。
あとは(１)同様、実際に作業を進めれば5回で終了することが分かります。

(３)
数が大きくなっていますが、試験場ではこれまで同様、慎重に作業を進めて求めるのが現実的かもしれません。

実は、素因数分解を用いると作業回数を簡単に求められます。
例のように8個ずつの場合、8＝2×2×2、
(1)のように40個ずつの場合、40＝2×2×2×5、
(2)のように96個ずつの場合、96＝2×2×2×2×2×3
のように、はじめにそれぞれが持っていた玉の数を素因数分解したときに含まれる2の個数の回数で作業が終わっています。
3072＝2×2×2×2×2×2×2×2×2×2×3と2を10個含むので、作業は10回で終わります。

【５】旅人算

(１)
B君が学校に戻り始める12分後、B君は学校から40×12＝480mの地点に、Cさんは50×(12－8)＝200mの地点にいて、2人の間は280m離れています。
280m÷(90＋50)＝2分より、B君とCさんはその2分後に出会います。
Cさんに注目すれば、200m＋50m/分×2分＝300mの地点で出会うと求められます。

(２)（３）
B君とCさんが出会ったとき、A君は学校から480＋20m/分×2＝520m離れた地点にいて、B君やCさんとは520－300＝220m離れています。
また、A君が学校に着いたときに、B君とCさんは30m/分×3分＝90m学校の手前にいます。
よってB君とCさんが出会ってから、A君が学校に着くまでの間に、220－90＝130mだけ差が縮んでおり、この間の時間は130÷(30－20)＝13分です。
あとは、容易な計算で答えを求められます。

【合否を分けた１題】

大問6を取り上げます。

【６】　平面図形

条件を満たす図形の範囲を求める出題でした。
慶應湘南藤沢の【６】としてはやや取り組みやすい難度でしたが、受験生間で差がつきやすい大問であったと思われます。垂直二等分線を活用することが後半を見通しよく解決する鍵を握ります。

（１）

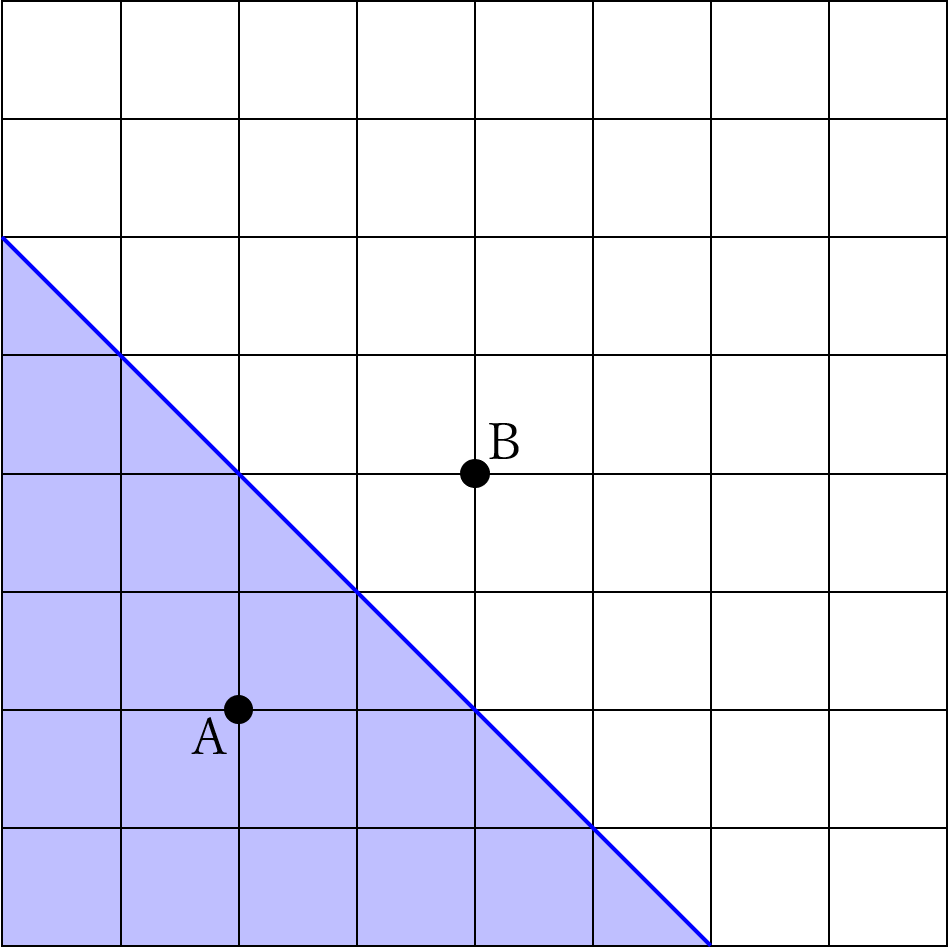
上図に示した青い線は、AとBからの距離が等しくなる点を集めた線、すなわちAとBの垂直二等分線です。この線よりも印Aに寄った側が求める範囲です。
これは直角二等辺三角形で、6×6÷2＝18㎠です。

（２）

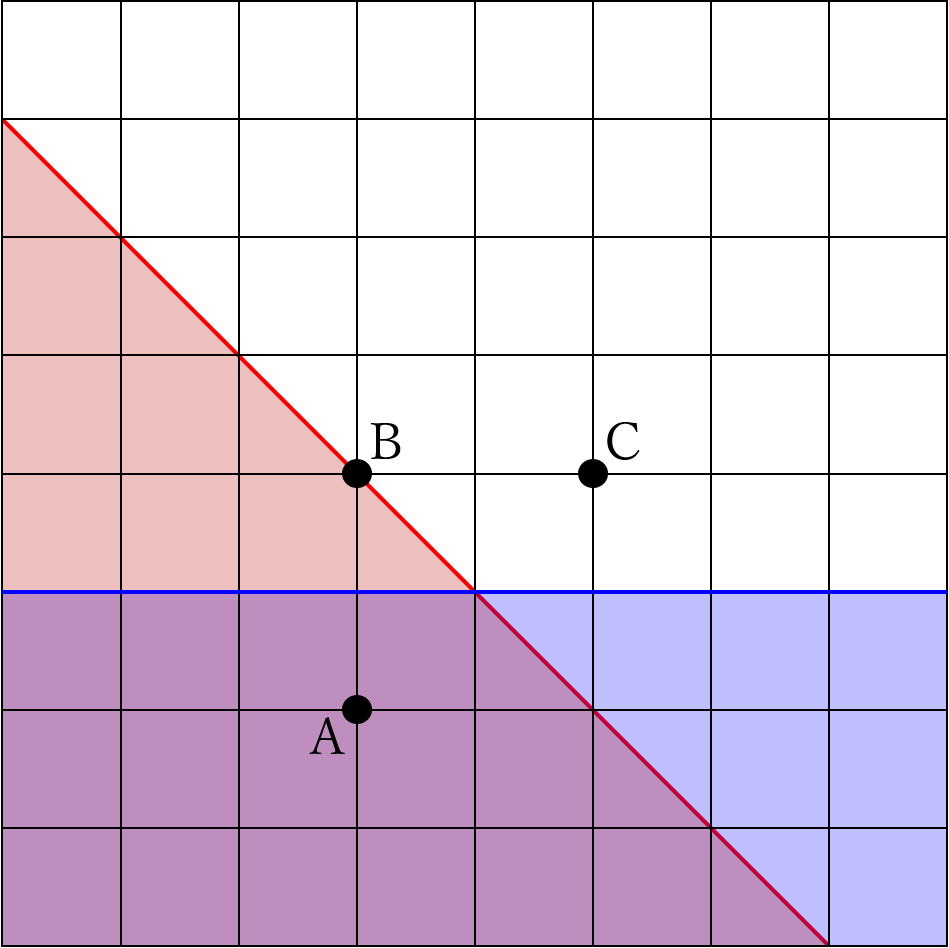
(１)と同様に垂直二等分線を引いて考えます。
青い線はAとBの垂直二等分線で、青く色づいた部分が「BよりもAに近い範囲」です。
赤い線はAとCの垂直二等分線で、赤く色づいた部分が「CよりもAに近い範囲」です。
求める範囲は、BよりもCよりもAに近い範囲ですから青と赤の共通部分です。
台形として、(4＋7)×3÷2＝16.5㎠と求められます。

BとCの垂直二等分線は解答には必要ないことも確認しておきましょう。

（３）

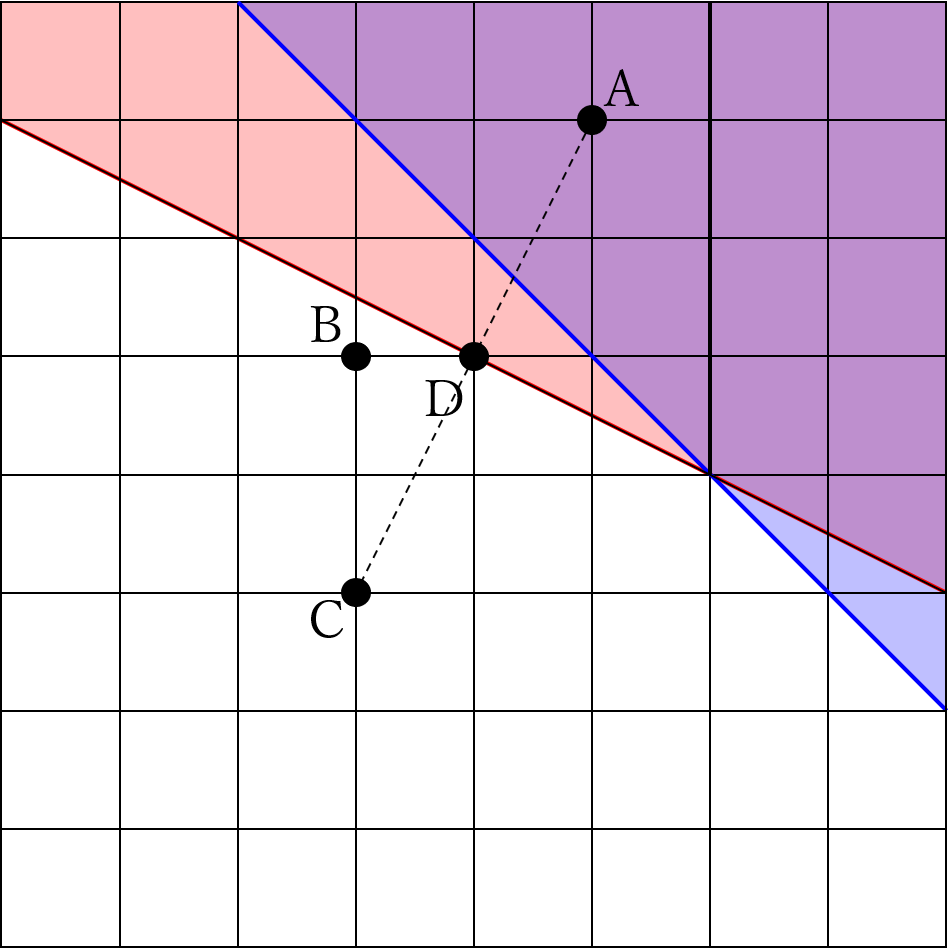
(２)までと同様に、AとB、AとCの垂直二等分線を引いて考えます。
AとCの垂直二等分線は、AとCの中点(上図のD)を通り、ACに直交するように書くことに注意しましょう。
上図で青と赤の共通部分の面積は、例えば黒い線で直角二等辺三角形と台形に分けるなどして求められます。
4×4÷2＋(4＋5)×2÷2＝17㎠です。

著者：桑田陽一

この記事は役にたちましたか？