算数の合否を分けた一題
慶應湘南中入試対策・算数の合否を分けた一題(2020年度)
難易度分類
| [1] | (1)A (2)A (3)A |
|---|---|
| [2] | (1)A (2)A (3)A |
| [3] | (1)A (2)A (3)A |
| [4] | (1)A (2)B (3)B |
| [5] | (1)A (2)A (3)B |
| [6] | (1)A (2)A (3)B |
A:SFC合格を目指すなら必ず得点したい問題
B:着眼点や解法ツールにより正答率・かかる時間に差がつく問題
出題総評
昨年から若干の出題傾向の違いがみられました。大問1は計算を含む小問が全3問(去年は計算+小問で全2問)、大問2は昨年と同じく一行問題が3問、大問3~6は例年通り4つの単元にわかれて、という形式の入試でした。
詳細については大問1が分数計算・逆算・立体図形、大問2が割合・和と差の文章題、大問3は規則性、大問4は割合の文章題、大問5は平面図形の問題、大問6は速さの応用問題でした。
問題別寸評
(1)は工夫の要る分数の計算、(2)は分数と小数の入り混じる逆算の問題、(3)は立体図形の基本問題でした。目安の時間としては5分ほどです。
(1)

(2)
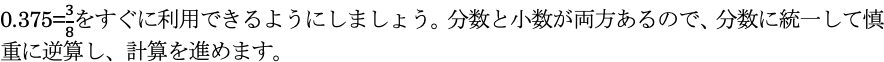
(3)
円柱の側面積を問われているので、長方形の面積を考えます。長方形の縦の長さは円柱の高さである40㎝、横の長さは円柱の底面である直径が28㎝の円の周りの長さと同じです。基本的な問題なので、(1)(2)も含めて落とすことはできません。
(1)は逆比を利用する割合の文章題、(2)はつるかめ算、(3)は集合算でした。すべて基本的なレベルであり、1つも失点は許されません。目安の時間としては7分ほどです。
(1)
1分あたりに入れる水の量は、最初とあとで1:1.2=5:6です。水そうの満水の量は一定なので、かかる時間は逆比で6:5となることを利用して答えを求めます。
(2)
進み方が5歩・3歩で2種類あり、表の出た回数と裏の出た回数の合計と全部で進んだ歩数がわかっているので、つるかめ算を用いればよいことがわかります。
(3)
金魚を飼っている人・飼っていない人、犬を飼っている人・飼っていない人とグループがわかれるので、集合算です。表かベン図を用い、整理して答えを求めます。
ここからは大問になります。パスカルの三角形と呼ばれる、代表的な規則性の問題です。
(1)
各段の和を取ってみると、1段目が1、2段目が1+1=2、3段目が1+2+1=4、4段目が1+3+3+1=8、5段目が1+4+6+4+1=16…となっており、2倍をすると次の段の和になることがわかりますので、これを利用すれば7段目の和が求まります。
(2)
35段目は35個、36段目は36個、37段目は37個、…73段目には73個のメダルがあるので、35から73までの和を求めれば答えとなります。間の数に注意をしましょう。
(3)
先ほどの和の規則を利用すると、4096の1段下の和は4096×2=8192です。どの段であっても一番右と一番左にあるメダルの数はすべて1であることを考えれば答えが求まります。
割合の単元から、仕事算の問題です。今年は本問を、合否を分けた一題として詳細を後述します。
折り返しの性質・正三角形・30°の利用・直角三角形相似を考える平面図形の問題。
(1)
BEとEFは等しく、また図2からBEとCFは平行なので、CFをFのほうに延長した先の点がBであることをふまえると、BE=BFとなります。ここから、三角形BEFは正三角形となるので、アの角度が求まります。
(2)
三角形AEGに着目してみます。図2の三角形AEGと、図3の三角形AEGは折り返しの考え方から合同です。角AEBは180-60×2=60°なので、角AEG=60÷2=30°です。角EAGは90°なので、角AGE=180-(30+90)=60°となり、三角形AEGにおいて30°の利用が使えることがわかります。60°をはさむ辺の比が1:2なので、AG:GE=1:2です。次に、角ABEは三角形ABEに着目すると180-(90+60)=30°となり、図3における三角形ABGを見てみると、角GAEが直角であることから角GABも直角です。角AGBが60°であることと、三角形AEG・三角形ABGにおいてAGが共通なのでお互いに合同であることがわかります。ここから、問われているAG:GDはAG:GEと同じですので、答えが求まります。
(3)

2人の動きを考える旅人算の問題ですが、途中で動きが制限されてしまう設定があるために、最終問として少し処理の多いものになっています。
(1)
家から橋Aをわたるまでに240m進むので、240÷20=12分かかります。この時点で8時50分+12分=9時2分となりますが、9時に橋が上がってしまうため、元の状態に戻る9時10分まで足止めをくうことになります。そのあと、橋が渡れるようになるので、店までの距離をK君の速さで割ればかかる時間がわかり、答えが求まります。
(2)
橋Aと橋B、それぞれの場合で考えます。
橋A…家を8時30分に出て、240÷15=16分より橋を渡り始めるのが8時30分+16分=8時46分とわかります。橋を渡るのに300÷15=20分かかりますが、9時に橋が上がってしまうので橋を渡り終えるのが8時46分+20分+10分=9時16分となります。店まで540mあり、540÷15=36分かかるので9時16分+36分=9時52分に店に着くことになります。
橋B…家を8時30分に出て、600÷15=40分より橋を渡り始めるのが8時30分+40分=9時10分とわかります。橋を渡るのに300÷15=20分かかり、渡り終えるのが9時10分+20分=9時30分となります(橋が上がっているのが9時~9時10分と9時30分~9時40分なので止まることなく渡れます)。店まで300mあり、300÷15=20分かかるので9時30分+20分=9時50分に店に着くことになります。
(3)
最終問ですが、まずはK君の場合を調べ、O君について考える、といったように手順が決まっているので難易度が高いものではありません。
K君は8時30分に家を出て、橋Bを渡り始めるのが600÷20=30分より8時30分+30分=9時ちょうどとなりますが、橋が上がり始めるのでその10分後の9時10分に橋を渡り始めることになります。店までの距離は300+300=600mなので、600÷20=30分かかることから店に着くのは9時10分+30分=9時40分とわかります。
問題文の条件から、O君は店に着くのが9時40分よりも前であることになります。橋の上がる時間を無視して考えてみると、歩く時間は(240+300+540)÷15=72分となり、家を出るのが9時40分-72分=8時28分となります。しかし、この場合だと橋を渡り始めるのが8時44分となり、橋を歩いている途中で10分間止まることになるので、店に着くのが9時40分+10分=9時50分となってしまい条件に反します。このことから、足止めをくわないようにするには、橋Aを渡り終えるのが9時ちょうどとなればよいので、そこから逆算して家を出た時刻を求めます。
合否を分けた一題
後半の大問群の中で、今回は大問4を合否をわけた一題として紹介しましょう。仕事算の応用問題として、問題内のどこを①として計算を進め、答えまで導いていくのかをしっかり考えなければならない一題と言えます。
(1)

(2)

(3)
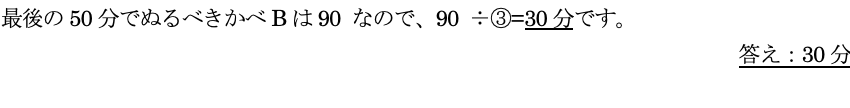
慶應湘南中入試対策・関連記事一覧
慶應湘南中入試対策・同じ教科(算数)の記事
慶應湘南中入試対策・同じテーマ(合否を分けた一題)の記事
- 社会の合否を分けた一題(2010年度)
- 算数の合否を分けた一題(2015年度)
- 社会の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2016年度)
- 国語の合否を分けた一題(2016年度)
- 理科の合否を分けた一題(2016年度)
- 国語の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2017年度)
- 社会の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2018年度)
- 国語の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2019年度)
- 理科の合否を分けた一題(2019年度)
- 国語の合否を分けた一題(2019年度)
- 国語の合否を分けた一題(2020年度)
- 理科の合否を分けた一題(2021年度)
- 社会の合否を分けた一題(2021年度)
- 算数の合否を分けた一題(2021年度)
- 国語の合否を分けた一題(2021年度)