算数の合否を分けた一題（2019年度）

算数の合否を分けた一題

慶應湘南中入試対策・算数の合否を分けた一題（2019年度）

難易度分類

［１］	（１）A　（２）A
［２］	（１）A（２）A（３）A
［３］	（１）A（２）B（３）A
［４］	（１）A　（２）A（３）B
［５］	（１）A　（２）A（３）B
［６］	（１）A（２）①A　②B　（３）C

Ａ：慶應義塾湘南藤沢中学校を目指すなら必ず得点したい問題
Ｂ：着眼点や解法ツールにより正答率・かかる時間に差がつく問題
Ｃ：難易度や処理量から判断して、一旦とばすべき問題

問題別寸評

例年通りの６題構成、難易度も例年並みでしょう。慶應義塾湘南藤沢中学校の算数に対応するためには、入試で定番とされる問題（典型題と言われる問題）を身につけるだけでは不十分で、見たことがない問題に対処する力も養っていかなければなりません。［１］［２］の失点は許されません。また、後半も少し難しいかな？と思えるBレベルの問題もほとんどが得点しておかないと厳しくなります。今回は、［６］が手のかかる問題でした。最終問の（３）は時間内の正解は難しいと思いますが、（２）ではとりあえず手を動かして答えを出してしまいたいところです。

問題別寸評

［１］

（１）

A
最大公約数を求めるだけです。すこし数が大きいので、素因数分解を用いましょう。

（２）

A
部分分数分解の計算が含まれています。間がなくなって端の分数の引き算をすれば答えがでるというものですが、分母が２ずつ離れているので、２で割る必要があるというところも、さっと対応したいところです。

［２］

（１）

A
正方形の折り返し図形と、相似を利用する問題です。どのテキストにも載っている典型題です。

（２）

A
男子３人、女子３人なので、「男、女、男、女、男、女」と「女、男、女、男、女、男」の２通りのパターンがあることに注意しましょう。

（３）

A
水の高さ４㎝、三角すいの高さ８㎝なので、相似比１：２の三角すいができています。
水の入っている部分の体積は全体の７／８になります。

［３］

（１）A（２）A（３）A

犬がつながれている問題はよく見かける問題ですが、ひもの付け根が自由に動かせるというちょっと変わった設定の問題でした。
ひもの付け根が固定されていれば、ひもの動きは円を描きますが、付け根が固定されていない場合は、ピンとヒモを張ったまま左右に移動できるので、平行線を描くことができます。これさえ押さえておけば、あとは慎重に作図するだけの簡単な問題です。
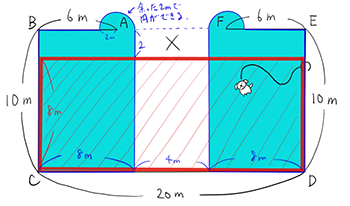
（3）の図は、このようになります。
犬がBCを動くとき、BAの壁についたとき、2mヒモがあまるので、これで柵の外に円を描くことができます。
従って、犬が動ける範囲は、長方形BCDEに円を二つ加え、そこから白い長方形を引くことで求めればよいので、
10×20+2×2×3.14−2×4＝204.56㎡

［５］

（１）A（２）A（３）B

川の形状を円状にした、流水算です。（１）、（２）とも形状が円というだけで、普通の流水算です。基本通りに確実に処理したいところです。
（３）は中学入試ではおなじみの30°、60°の直角三角形を利用することに気が付けるかどうかがポイントになります。難易度はBとしましたが、実質的には［５］は全部正解しておかないと合格は難しいのではないかと思います。

［６］

いわゆる「最適解」を求める問題でとくに「こう」という解法がないタイプの問題です。とくに（３）は厳密に検証するとかなりの時間を要することになり、テスト時間内での解答はかなり厳しいと思われます。若干気持ち悪さはありますが、テスト時間を考えると、当たりを付けて答えてしまうというのが現実的なところでしょう。

（１）

すべてのパイプが同じ量なので、A６本＝６、Ｂ＝５、Ｃ＝３　合計１４と表しておくと、Ａの分量は、６／１４＝３／７です。

（２）

分数のままだとやりにくいので、タンクの全体の量を整数にします。
6×60＋5×60＋3×60＝840 より、薬全体の量を840とします。

①
Aを4本、Bを5本、Cを3本使って、Aを360、Bを300、Cを180入れます。
全ての管を同時に使えるのは、どれか一種類の薬が満タンになるまでです。
BとCを60分入れると、それでBとCの必要量は全て入ることになるので、残りはAだけです。
360-4×60＝120、120÷4＝30分
よって答えは、ABCを60分同時に入れて、その後Aだけを30分入れるとなります。

②
Aを5本、Bを4本、Cを3本使います。
満タンになるまでの時間は、Aが72分、Bが75分、Cが60分です。
なので、全部の管を使えるのは、60分までとわかります。
すべて60分使うと、Aは残り360−5×60＝60、Bは300−4×60＝60 となっています。
次はA、Bを一緒に12分使ってAは満タンになり、Bが60−4×12＝12残るので、
12÷4＝3分で終了です。
よって答えは、ABCを同時に60分入れて、Cを止めて12分入れ、Aを止めて3分入れる。です。

（3）

作業を早く終わらせるには、パイプの本数の配分を、薬品の成分の割合に出来るだけ近づけておくことが理想です。
Aは全体の3/7を占めるので、23× 3/7≒9.8本、
Bは 23× 5/14＝8.2本、Cは23× 3/14 ＝4.9本がそれぞれ理想的な本数です。
この本数に近い数字で当てはめて計算してみます。
まずは四捨五入した値でAを10本、Bを8本、Cは5本としてみます。（合計23になっているかも確認します。）
10×36＝360、８×36＝288、５×36＝180となり、
最初の36分で、AもCも満タンになるので効率が良さそうです。
残りのB12は、12÷８＝1.5分なので、合計37.5分でいっぱいになります。
最後の端数の時間も短いので、この入れ方が最も早く終わる入れ方のように思えますが、
もう少し検討して、Aを９本、Bを９本、Cを５本も一応確認してみます。
この場合は、Bの満タンに300÷９＝33.3…＝33分20秒かかり、このときAが300、Cが166.6…入ります。このあと、Cが13.3…÷５＝8/3分で、2分40秒で満タンになり、Aは60ー８/３×9＝36、36÷９＝４で、あと４分で満タンです。
よって、合計で、33分20秒＋２分40秒＋４分＝40分となり、先ほどより少し遅くなりました。答えは、37.5分とできます。ただし、これは厳密に最短の時間であるというには検証が不十分な可能性がありますが、Cを４などに減らした場合、AとBが先に満タンになり、Cの残りを入れるのに、少ない割合で入れることで余計に時間がかかると予想できます。したがって、Cを減らす場合は検討する必要がないと予想できます。

合否を分けた一題

今回合否を分けたのは、正確な作業力を要する［４］だったと思います。

［４］

（１）A（２）A（３）B

（１）題意通りに作業すれば簡単に正解できます。ここは慎重にいきましょう。

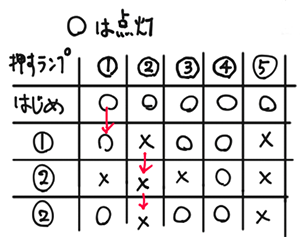
押したランプはそのままになるので、まず押したランプの下にそのまま同じ記号を書き、その両隣のランプの◯と×を逆にしていく。というような作業です。
以上より、ついているランプは3つあります。

（２）

少々長くなりますが、これも頑張って作業してしまえば、正解できます。
ここまではとりたいところです。

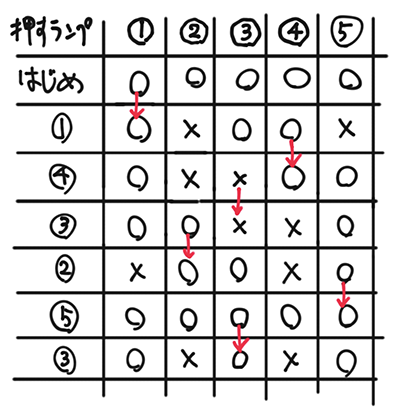
（1）と同様に作業していけば、表通りついているランプは①、③、⑤です。

（３）

最後に③を押すことで全部のライトがつくように、その直前の状態を遡って作ればよいわけです。
しかし、この最後の部分だけを考えればよいかというと、最後の③→□→③の部分で、はじめの③のときにどうなっているかを調べるには結局全部書き出す必要があります。ですので、調べ上げにはかなりの時間を要してしまいます。
他に良い方法はないでしょうか？

実は、ライトがついているか消えているかを決定するのは、そのライトの隣のボタンが何回押されたかに左右されます。たとえば、①→②→③→①と押したときに、⑤が消えているかついているかは、⑤の隣のボタンを偶数回押したのか、奇数回押したのかで決まるわけです。この場合は、⑤の隣である①のランプを2回押しているので、⑤は点灯しています

このように考えると、
①→③→④→①→⑤→②→③→②→③→④→①→①→②→①→⑤→②→⑤→②→③→□→③　の最初から最後までに、それぞれのボタンが押された回数を調べます。
①＝５回、②＝５回、③＝５回、④＝２回、⑤＝３回　です。
①のランプは、②と⑤を押したときに点灯･消灯します。②と⑤のランプは合計で８回（偶数回）押しているので、①のランプはついています。
ほかのランプも全部同じように調べていくと、
②のランプは、①と③→合計１０回（偶数）＝点灯
③のランプは、②と④→合計７回（奇数）なので、このままでは消えています。
④のランプは、③と⑤→合計８回（偶数）＝点灯。
⑤のランプは、①と④→合計７回（奇数）で消えている。
ですので、③と⑤のランプを点灯させるには、その間の④のボタンを押せば良いので、□は④が入ります。

（3）はこの解法に気付けば、かなり早く処理ができ、しかも確実に答えられるのですが、実際は手作業で書き出した人の方が多いでしょう。
合否の分かれ目としては、やはり日頃から正確な作業、整理整頓された書き方を練習しているかどうかだと思います。

著者：受験Dr. (受験ドクター)

この記事は役にたちましたか？