算数の合否を分けた一題（2018年度）

算数の合否を分けた一題

慶應湘南中入試対策・算数の合否を分けた一題（2018年度）

難易度分類

［１］	(1) A　　(2) A　　(3) A
［２］	(1) A　　(2) A　　(3) B
［３］	(1) A　　(2) A　　(3) B
［４］	(1) A　　(2) A　　(3) B
［５］	(1) A　　(2) A　　(3) B
［６］	(1) A　　(2) A　　(3) B

Ａ：慶応藤沢中等部合格を目指すなら必ず得点したい問題
Ｂ：着眼点や解法ツールにより正答率・かかる時間に差がつく問題

総評

大問６題、小問１８題という問題構成であった。慶応藤沢中等部は難問奇問の出題はなく、平易な問題が多く出題されます。平易な問題をどれだけスピードと正確性をもって解答していけるかが勝負のカギとなります。時間をかければ正解にたどり着くという学習をしていては試験時間内にすべての問題に目を通すことは難しいでしょう。かつ高得点勝負になることが予想されるのでミスがそのまま致命傷になりかねません。普段からミスは絶対にしないという気持ちをもって学習に取り組んでください。

問題別寸評

【１】四則計算を含む小問集合

(１) 逆算　（２）円の面積　(３)相当算
いずれも見たことがある平易な問題です。
全問正解することが望ましいです。

【２】小問集合

(１) 分配算（２）植木算　（３）整数の性質

（３）の整数の性質について解説します。
□602□の5桁の数値で、2人で金額を出し合うので１の位は偶数です。
そして４５個分の金額ですので５の倍数ですから1の位の数字は０だとわかります。
また、４５＝３×３×５なので5桁の数値は9の倍数であることがわかります。
9の倍数は、各位の数の和が９の倍数だから万の位の数字は１だとわかります
45人分のケーキの値段が16020円なのでケーキ1個の値段は、
１６０２０÷４５＝３５６円

【３】数列

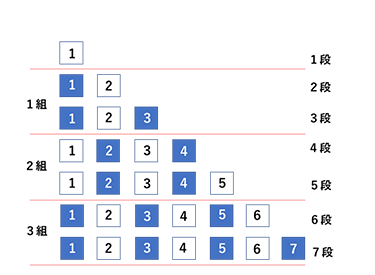
（１）最初の黒い５のカードは6段目の５です。
　　6段目の最後から2番目なので　（１+６）×６÷2　–　１＝20番目

（２）白と黒が交互に並んでいるので、白いカードの30番目は全体の59番目のカードになる。
１０段目までにカードは５５枚あるので、11段目の4枚目になります。よって　４

（３）白い２のカードは9組の下段に位置します。9組の下段は19段目ですので
１９段目の2番目ということになります。
（１+１８）×１８÷２　＋　２＝１７３番目

【４】平面図形

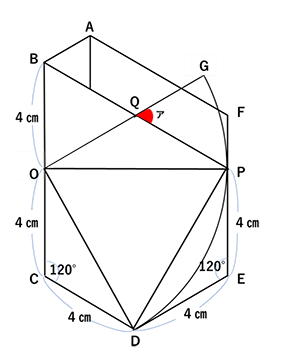
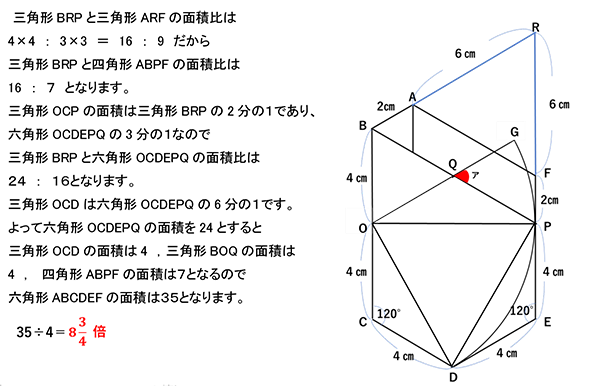
（１）角ＯＣＤ＝角ＰＥＤ＝120°だから
三角形OCDと三角形PEDは合同となり、
OD＝PDだとわかります。また、辺ODと辺OPは四分円
の半径だから三角形ODPは正三角形になっています。
角COD＝30°角DOP=６０°より　角BOP＝90°
同様に角CDP＝90°だから三角COPと三角形CDPは　
合同になります。よって角CPO＝３０°だとわかります。
また、三角形CPOと三角形BPOも合同ですから、
角BPO＝角CPO＝３０°
三角形BPOは角が３０°６０°の直角三角形だから
BPの長さはBOの長さの２倍になるのでBP＝８㎝。
点QはBPの真ん中の点だからPQ＝４㎝
角DOG＝90°角DOP＝60°より角QOP＝30°となります。
ここで角QOP＝角QPO＝30°だから三角形QOPは二等辺三角形なので
OQ＝PQ＝４ｃｍとなります。。

（２）
（１）よりBO＝OQ＝BQ＝4㎝だから三角形BOQは正三角形だとわかります。
　角BQO＝角ア＝60°

（３）

　　

【５】水の深さ　（速さのつるかめ算）

【６】速さと比　（流水算）

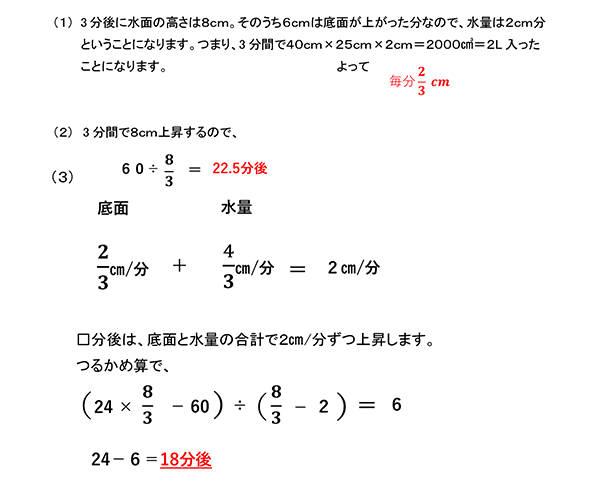
(ア) 船Ａの上りにかかる時間は180分、下りにかかる時間は90分ですから
速さの比は時間の比の逆比で　１：２である。
上りを1分間②進む速さだとすると下りの速さは④、静水時の速さは③、
川の流れの速さは①となります。
よって船Ａの静水時の速さは、川の流れの速さの３倍になります。

(イ) 船Ｂの上りにかかる時間は120分、下りにかかる時間は72分ですから
速さのひは時間の比の逆比で　３：５である。
（１）より川の流れの速さは①とすると、船Ｂの上りの速さは③、下りの速さは⑤、
静水時の速さは④になります。

（２）船Ａ、船Ｂの様子をダイヤグラムで表すと次のようになります。

　　　　　
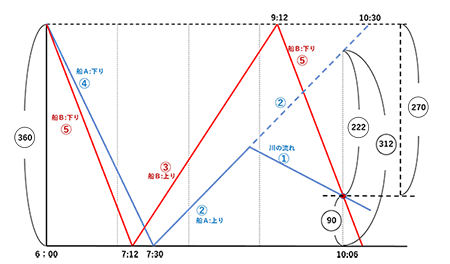
船Ａがもし故障していなければ、１０時６分にはＱ地点から
②×１５６分＝312ほど離れた地点にいます。また、船Bが9時12分から10時6分まで
に進んだ距離は⑤×54分＝270　です。　船Bが船Aに追いつくのは、３６０－２７０＝９０　でQ地点から９０の距離の地点です。10時6分に船Aと船Bは３１２－９０＝２２２の距離離れていることがわかります。これは、船Aが動かなくなってから10時6分までの間に船Aと船Bが1分間で　①＋②＝③ずつ離れていったことによります。
この時間は、２２２÷３＝７４分かかったことになります。
したがって、船Aが動かなくなった時間は　10時6分－74分＝8時52分となります。