算数の合否を分けた一題（2016年度）

算数の合否を分けた一題

慶應湘南中入試対策・算数の合否を分けた一題（2016年度）

難易度分類

［１］	（１）A　　（２）A
［２］	（１）A　　（２）A　　（３）A
［３］	（１）A　　（２）A　　（３）B
［４］	（１）A　　（２）A　　（３）B
［５］	（１）B　　（２）B　　（３）A
［６］	（１）B　　（２）C　　（３）C

A…慶応湘南藤沢中合格を目指すなら必ず得点したい問題
B…着眼点や解法により正答率・かかる時間に差がつく問題
C…難易度や処理量から判断して、後回しにしたほうがよい問題

問題別寸評

［１］

（１）小数・分数が混在している逆算の問題になります。確実に得点すべき問題です。

（２）平方数を探す問題です。　だいたい1800に近い平方数から予測して数字を見つけるようにしましょう。また、一の位が9であることから、□3×□3か◇７×◇７になります。□とに１，２，３，４・・・を入れて解いていってもいいですが、1800に近いとなると、□＝4が見つかるでしょう。◇にも１，２，３，４・・・といれていくと、こちらは当てはまるものがないので、43×43が正解となります。

［２］

（１）同じ金額のお金を持っているということと、
A＝　２０ポンド　＋　２２０００円
B＝　７０ポンド　＋　１２８００円

差は　５０ポンドが９２００円になります。　ここから１ポンド＝１８４円を求めれば簡単です。

（２）ご石の数が４６４個なので、同じ数ずつ４ブロックに分けると、４６４÷４＝１１６個
１１６÷４＝２９　２９＋４＝３３個・・・一辺に並んでいる個数となります。

（３）くるった時計の問題です。比例でも解けますが、相似形を作ってもよいでしょう。

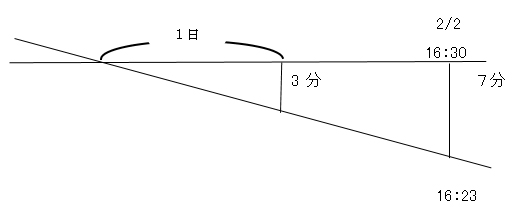
3分：7分＝24時間：□時間
□＝7×24÷3＝56時間

となります。56時間÷24時間＝2・・・8時間
つまり2日と8時間前です。　1/31　8：30

［３］

（１）影の問題は、相似形を見つけることがポイントになります。

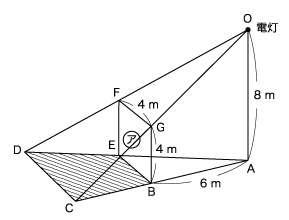
三角形CGBと三角形COAは相似なので、相似比は４ｍ：８ｍ＝１：２
また、三角形OFGと三角形ODCも相似　よって、OG:OC＝１：２
FG：DC＝１：２
なので、DC＝4×2＝8m

（２）台形DCBE＝（４+８）×６÷２＝３６㎡

（３）こちらも相似形を見つけましょう。

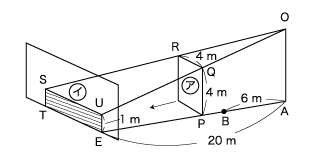
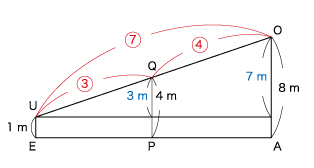
相似形よりOQ:OU＝4:7　となるので、RQ：SU=4:7
よって面積は、１ｍ×７ｍ＝７㎡

［４］

（１）（２）は、基本レベルになります。　ただ、おうぎ形が移動したときの図が描けないと正解にはたどり着かないでしょう。日頃から図を描いて解くという習慣をつけておく必要があります。

（１）

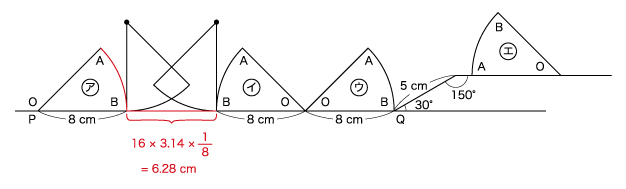
8×3+16×3.14÷8＝24+6.28＝30.28㎝

（２）ア～イまでのおうぎ形の面積は、下図のようになります。

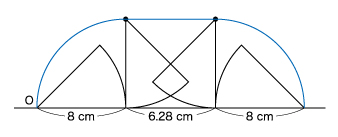
8×8×3.14÷4×2+8×6.28＝（32+16）×3.14＝48×3.14＝150.72㎠

（３）ウ～エまでのおうぎ形の動きは、下図のようになります。

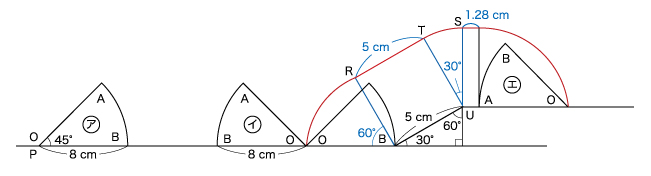
角OBR＝180°－（30°＋90°）＝60°
角TUS＝180°－（60°＋90°）＝30°
となります。その図が正確に描けたかどうかが、この問題のポイントになります。

［５］

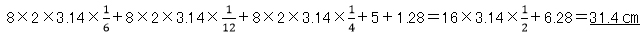
カードの並び方と作業の規則性を読み取りましょう。
こちらは合否を分けた一題で詳しく見ていきます。

［６］

退場する時間は、8分、14分、20分・・・というように6分ごとなので、出ていく班の番号を付けていくと、

	①	②	③	④	⑤	⑥	⑦	⑧
退場	8分	14分	20分	26分	32分	38分	44分	50分
バス発車		14分		29分			44分

（１）客は、6分ごとに班ごとに出てくるので、
8＋6×(22－1)＝134分＝2時間14分

（２）14、44、・・・となっているので、30分ごとに同時になる。
よって、14、44、74、104、134の5回

（３）退場する人数を①、バスに乗った人数を１とすると、
（②－１）×5＝⑦－３
⑩－５＝⑦－３
③＝２　よって1.5＝１
ということは、1.5の人たちが1回のバスに乗り込んでいるということなので、
22÷1.5＝14・・・1　つまり、14＋1＝15回で全員がバスに乗り終わる。
バスは15分ごとにきているので、14分＋15×（15－1）＝224分＝3時間44分

合否を分けた一題

2016年度の問題は、例年通り、基本的な問題が前半を占め、後半手を動かして調べたり、書き出したりという作業を伴う問題のセットでした。その中で、[５]が、手を動かし、規則性を探り、それを自分で式に表すことができるかということを問う良問だったと思います。この種の問題を事前に練習している受験生は、ここでも、「規則があり、それを見つければ簡単だ」という思考で解くことができるのですが、やり慣れてないと、すべて書き出してしまったり、書き出している途中でわけわからなくなったりと混乱をきたして飛ばしてしまったという生徒も多かったようです。

それでは、解説です。

［５］

（１）１～９までを書かせて、規則を見つけさせる問題になっています。

１　２　３　４　５　６　７　８　９
１　３　５　７　９　２　４　６　８
１　５　９　４　８　３　７　２　６
１　９　８　７　６　５　４　３　２
１　８　６　４　２　９　７　５　３
１　６　２　７　３　８　４　９　５
１　２　３　４　５　６　７　８　９

といことで、６回です。では、ここで２がどのような動きをしていうか確認しておきましょう。
２は、はじめ２番目、次に半分よりも＋２÷１番目、・・・となっています。

つまり、偶数番目の時は、次は、半分＋偶数番÷２
奇数番目の時は、次は、（奇数番＋１）÷２
となっていることに気づけたでしょうか。

（２）（１）より２がどこにあるかという規則から、３４と６６もわかります。
１～１００までのカードを並べるので、半分は１００÷２＝５０
２は、偶数番目なので、５０＋２÷１＝５１となり次は５１番目のところに並んでいます。
更に、５１は奇数番目なので、（５１＋１）÷２＝２６となり次は２６番目のところに並んでいます。
それをどんどんやっていくと、
２→５１→２６→６３→３２→６６→８３
３４→６７→３４→６７→３４→６７
６６→８３→４２→７１→３６→６８
つまり、２，３４、６６は並んでいるので、５回目

（３）(２)がわかれば、（３）は簡単です。
今度は、１～１２８枚のカードを並べているので、
１２８÷２＝６４が半分

２→６５→３３→１７→９→５→３→２

よって、７回目

やり方を知らなくても、まずは並び方に何か規則がないか疑って、（１）で９までの数字で考えさせるという流れになっています。「自分で考える」ということを促す良い問題ではないでしょうか。

こういった問題にどう対応するか、途中で投げ出してしまうのか、粘って解けるのかということを学校側は見ているのだと思います。やり方や○○算を知っているだけでは対処できない問題を日頃から取り入れて練習していきましょう。

著者：佐々木裕子

この記事は役にたちましたか？