算数の合否を分けた一題
渋谷中入試対策・算数の合否を分けた一題(2020年度)
難易度分類
| [1] | (1) A (2)B (3)A (4)B (5)A (6)A |
|---|---|
| [2] | (1) A (2)B |
| [3] | あA いA うA えA おB かC きC くA けA |
| [4] | (1) A (2)A (3)A (4)B |
A:渋谷教育学園渋谷中合格を目指すなら必ず得点したい問題
B:着眼点や解法ツールにより正答率・かかる時間に差がつく問題→合否を分けた一題
C:難度・処理量から判断して、得点差がつかない、合否に影響を受けない問題
出題総評
今年度は比較的解きやすい問題の構成でした。例年ですと、1問取り扱いにくい問題がでてくるのですが、今回は、そこまで難易度も高くなく、しっかりと条件を読み取って問題文に即して解き進めれば得点できたという問題が多かったと思います。その中で、得点差が出たのではないかという問題が【2】の点の移動の問題です。後程、「合否を分けた一題」で取り上げます。また、【3】の場合の数もやや時間がかかり得点差が開いた問題ではないかと思います。ただ、【4】が実は簡単な問題で、【3】で時間をかけてしまうよりも先に【4】を確実に解き切っていた方が得点にいい影響が出たのではないかと思います。その辺りの「判断」、どちらを先に解くのかという見極めが必要だったとも言えます。先の問題ばかり気になるのもよくないですが、時間配分ということも試験では必要になってきますので、どの問題を先にやった方がいいのかという「判断力」もつけていきましょう。
問題別寸評
(1)四則演算の長い式
(2)
素数、素因数分解を利用する問題です。2020を素因数分解し、ある2けたの整数□□との積が0と1しか用いない整数という条件から推測していきます。
(3)
半径のわからない円の面積は、半径×半径=対角線×対角線÷2という正方形の面積を利用することを思い出しましょう。
(4)場合の数
A×B⇒4の倍数 B×C⇒9の倍数
サイコロは、1,2,3,4,5,6の目しかないので、条件に合うように場合分けしていきます。
A=4の時、B×C=(3,3)、(3,6)、(6,6)、(6,3)の4通り
A=2の時、B×C=(6,3)、(6,6)の2通り
A=6の時、B×C=(6,6)、(6,3)の2通り
よって8通り
(5)食塩水の問題
Aの食塩水の食塩の量は18g
Bの食塩水の食塩の量は9g
どちらも10gずつ水か食塩水を入れていくとき、Aの食塩の量は変わらない18gなので、Bの食塩の量も18gになれば、濃度が同じになります。
10gに入っている食塩の量は10×0.08=0.8g
(18-9)÷0.8=11.25分⇒11分15秒後
(6)四捨五入
四捨五入で求める場合、ギリギリの範囲まで考えることがポイントです。
四捨五入して1230円になるということは、1225以上1235未満。
また、四捨五入して1260円になるのは、1255以上1265未満。
未満まで考えて、合計が入る範囲を求めましょう。
こちらは合否を分けた一題で取り上げます。
あ⇒〇の色が黒か白かの2通りあるので、2×2×2×2×2×2=64、全部白の場合は除くので、64-1=63通り
い⇒4か所のうち2個黒になる場所は、形が同じものは除くので、4通り(たてに2つ、横に2つ、右斜めに2つ、左斜めに2つ)
う⇒4点のうちの3点が黒の時、1点白にすればいいので、4通り
え⇒以上を全て足して、1+4+4+1=10通り
お⇒6点のうち2点が黒の場合、同じ形になってはいけないので、書き出すと、7通り
か⇒6点のうち3点が黒の場合、6×5×4÷(3×2×1)=20通り、ただ、同じ形になるものは除くので、5個同じものができる。よって、20-5=15通り
き⇒6点のうち4点が黒の場合、6×5÷(2×1)=15通り。ただ、同じ形になるものを除くので、1つ同じ形になるので、15-1=14通り
く⇒6通り
け⇒1+7+15+14+6+1=44通り
【3】の「場合の数」に時間をかけるよりも、実は先に【4】をやった方が得点できる問題でした。
(1)
(1)はABを軸として三角形ABCを回転したときの体積。
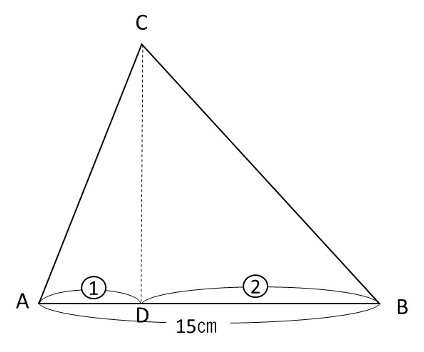
(2)
(2)はSRを軸として三角形PQRを回転した時の体積。
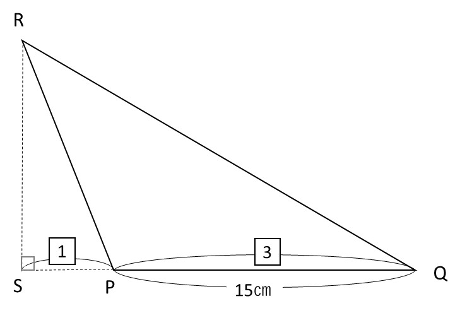
どちらの三角形も面積が75㎠と問題に書いてあるので、高さは10㎝とすぐ求めることができます。
この(1)、(2)は、5年生でも解けるレベルでしょう。
特筆すべき問題は、(3)、(4)になります。
点Aと点P、点Bと点Qがそれぞれ一致するように、辺ABと辺PQをぴったりあわせ、三角形ABCと三角形PQRを重なる部分ができるようにおきました。重なる部分を図形㋐とします。
(3)AB(PQ)を軸として図形㋐が1回転させてできる立体の体積は何㎤ですか。
(4)SRを軸として図形㋐を1回転させてできる立体の体積は何㎤ですか。
という問題が続きます。
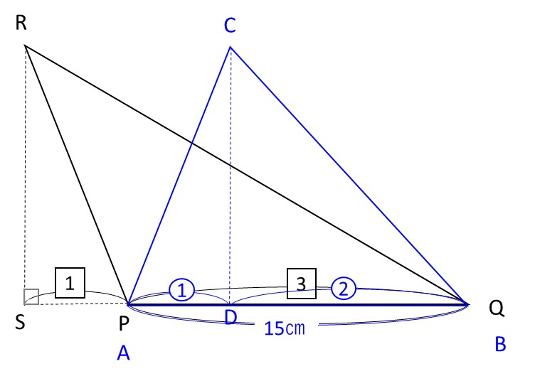
点Aが点Pに、点Bが点Qに重なるように移動しました。
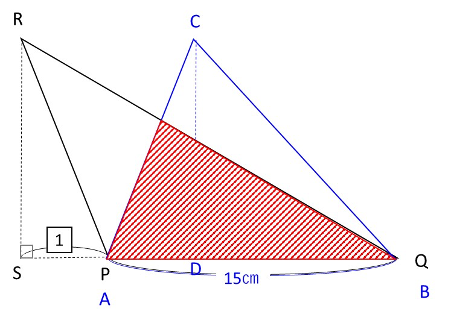
(3)の重なる部分は、図の赤い斜線部分になります。
これを、ABを軸として回転したときの体積は、高さを求めればあとは簡単です。
高さは、相似形を利用して求めましょう。
下の図の直線HGが三角形HABの高さになります。三角形HCRと三角形HABは相似形です。相似比は、RC=10㎝、AB=15㎝なので、10:15=2:3となり、高さの比も2:3
よって、10㎝÷5×3=6㎝となります。
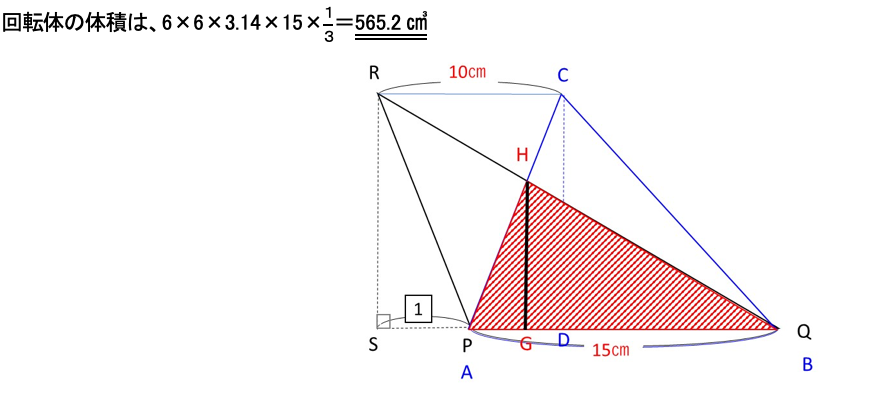
(4)も完成図をまずは描いて求める部分の形を示しましょう。
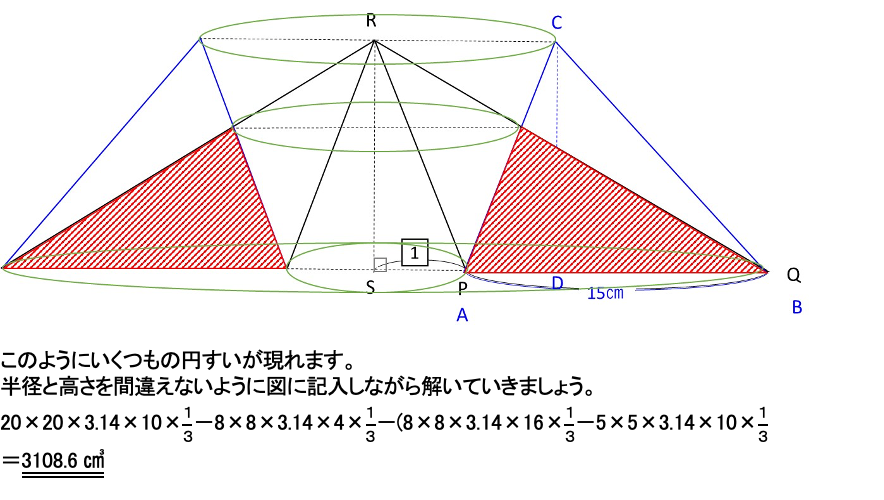
合否を分けた一題
【2】は、点の移動と周期の問題です。
(1)
点Pは毎秒1㎝で正方形ABCDをBからA,D,Cの順に動きます。
点Pが初めの位置点Bに来るのは16㎝÷1=16秒ごと
点Qは毎秒1㎝で、正方形の1辺FEを往復するので、初めの位置点Fにくるのは、
6+6=12㎝、12㎝÷1=12秒ごと
よって、16と12の最小公倍数ごとに同じ位置にくるので、初めて最初の位置にくるのは48秒後
(2)
2つの正方形をどちらも2等分する直線上に点Pと点Qがいるのは、正方形の対角線上にいないとあり得ないということがわかります。ここに気づけたかどうかがポイントです。
(3)
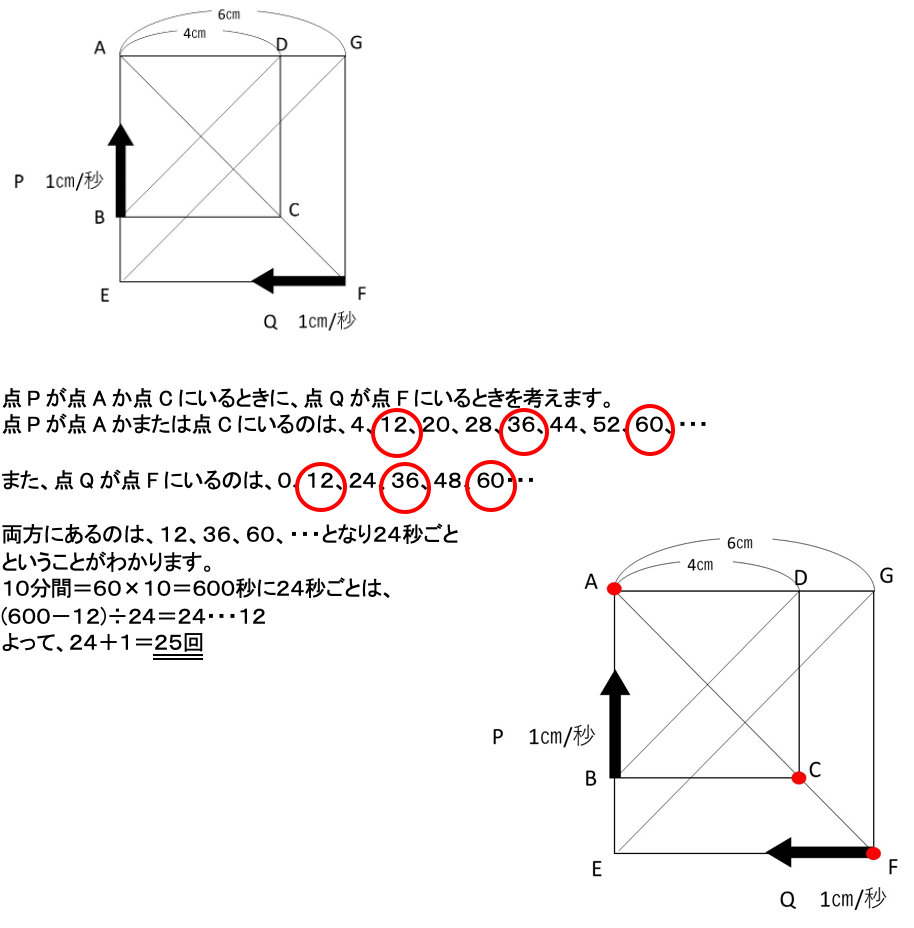
次に、三角形GPQが正方形AEFGの面積の半分になるということは、
辺GPが辺GAになるとき、つまり点Pが点Aに来たとき
または、
辺GQが辺GFになるとき、つまり、点Qが点Fに来たとき
この2つのパターンしかないということに気づけるかどうかがポイントです。
1)点Pが点Aにいるのは、
4、20、36、52、68、・・・
1分間なので、68秒以外全部OK
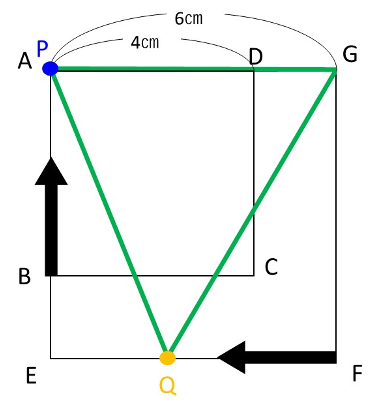
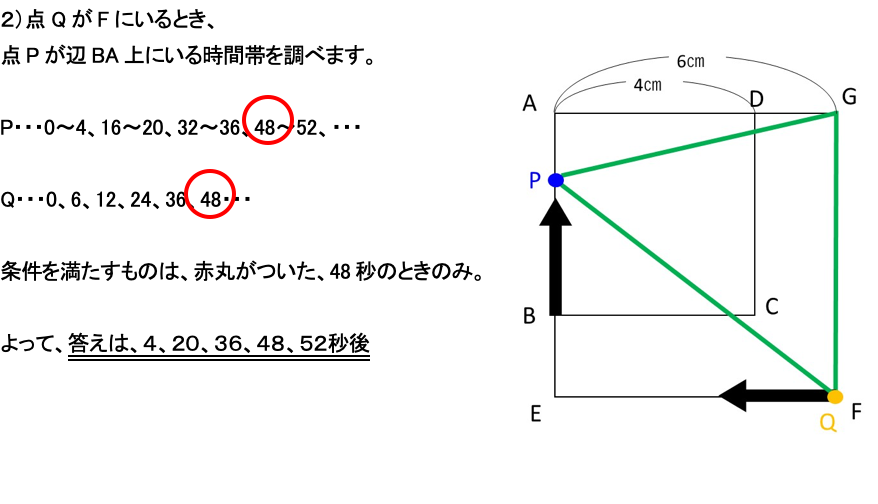
2)点QがFにいるとき、
渋谷中入試対策・関連記事一覧
渋谷中入試対策・同じ教科(算数)の記事
渋谷中入試対策・同じテーマ(合否を分けた一題)の記事
- 算数の合否を分けた一題(2016年度)
- 国語の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2016年度)
- 理科の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2017年度)
- 国語の合否を分けた一題(2017年度)
- 社会の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2018年度)
- 国語の合否を分けた一題(2018年度)
- 理科の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2019年度)
- 社会の合否を分けた一題(2019年度)
- 国語の合否を分けた一題(2019年度)
- 理科の合否を分けた一題(2020年度)
- 国語の合否を分けた一題(2020年度)
- 社会の合否を分けた一題(2021年度)
- 理科の合否を分けた一題(2021年度)
- 算数の合否を分けた一題(2021年度)