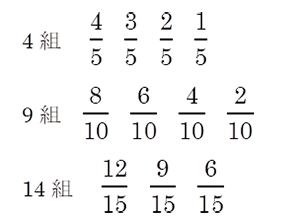算数の合否を分けた一題
渋谷中入試対策・算数の合否を分けた一題（2019年度）
難易度分類
| １ | (１) A (２) A (３) A (４) A (５) B |
|---|---|
| ２ | (１) A (２) A (３) A (４) B |
| ３ | (１) B (２) B (３) B (４) C |
| ４ | (１) A (２) A (３) B |
Ａ：渋谷教育学園渋谷中に合格を目指すなら必ず得点したい問題
Ｂ：着眼点や解法ツールによりかかる時間に差がつく問題
Ｃ：難易度や処理量から判断して、一旦とばすべき問題
2019年度 出題総評
大問３では、国民にマイナンバーを割り振るという、数の操作の問題が出題されています。
対応力、作業力の両方が要求される問題でした。
それ以外は、受験生ならどこかで見たことのある問題が並んでおり、対策可能なものばかりと言えます。標準的な解法パターンを身につけ、与えられた情報を正確にとらえ、緻密な作業ができれば、得点を重ねることができます。算数を苦手とする受験生にも、練習次第で大いにチャンスがある出題構成です。
2019年度 問題別寸評
(１) 計算
0.4375でどうするか迷うところです。このまま思い切って筆算に「突入」するなら、ほかの設問の後に回した方が賢明です。どうしても工夫したい場合ですが、
375という数字の並びに注目しましょう。
0.375＝3/8を利用して、
0.0375＝3/80と処理できます。
0.4＝32/80ですから、
0.4375＝3/80＋32/80＝35/80 これで0.4375が分数になってくれました。
(２) 平均の速さ
確実に得点したい問題です。
(３) 整数
あと2大きければ7でも13でもわり切れます。
(４) 食塩水
こちらも確実に得点したい問題です。
(５) 売買
２種類の価格で販売している状況を整理しましょう。
(６) 数列
分母2、分母3、…とグループ化して、群数列ととらえましょう。各組の個数は
1,2,3…と増えていきますから、特定の組までの個数の合計はいわゆる「三角数」です。13組までの個数の合計は、1＋2＋3＋…＋13＝91になりますから
100＝91＋9より、100個目の分数は
14組の9番目
にくることをしっかり押さえましょう。
14組の9番までに存在する、約分して分母が5になる分数を書き出すと、
の11個です。この合計を求めます。
練習していればすぐに答えに到達できます。体積でなく、比を求めます。計算ミスの心配がなく、実力通りの差になります。
(１)
柱体なので、底面積に注目します。手前の面ADHEを1：3に分割しています。
(２)
(３)
立方体の上部に同じ立方体を積み重ねて切り口を延長すると、求める立体が三角すい台になっているのがわかります。三角すい台の体積は
大きな三角すい － 小さな三角すい
で求めるか、相似比・体積比を利用するか、いずれかの方法で求めるのが一般的です。
(４)
一般に切断面が２枚以上になるとイメージしにくく作図しづらいため、正解率は大きく下がります。十分な訓練を積んでこのレベルは普通に正解できるようになっていると心強いです。
270°のおうぎ形２個が合わさった複合図形を回転させます。
（１）
この問題は確実に取りましょう。
（２）（３）
回転後の位置に図形Fをかき、対応する点を90°の弧で結ぶと求める図形ができます。
図が要求されているので、ていねいに描いて、計算もていねいに行いましょう。
問題そのものは難しくないので、ミスをしないことが大切です。
合否を分けた１題
大問３を取り上げます。
「法則」という名のルールが与えられていますので、忠実に運用しましょう。
(１)
ルール運用の確認問題です。
「法則」に従って、上5桁を計算し、一の位の数字があっているか見ます。
(２)
「法則」に従って計算してみます。
3×6＋2×5＋□×4＋4×3＋6×2＝52＋□×4
これを11で割った余りを11から引いたものが9なので、
52＋□×4 を11で割った余り＝2とわかります。これより、
□＝4を求めることができます。
(３)
力の差がはっきり出そうな問題です。
申告した数字 173591に対する、正しい数字の候補をあげ、すべての候補をチェックします。（＊）
| 誤りのある位 | 正しい数字の候補 |
|---|---|
| 十万 | 473591 |
| 万 | なし |
| 千 | 176591 |
| 百 | 173891 |
| 十 | なし |
| 一 | 173594 |
4つの候補のうち、一の位が「法則」の条件を満たすものは176591でした。
(４)
結論を予想し、理由も説明しなければなりません。どちらの結論になるのか、ここまでの設問から探るとすると、（３）で行った作業
一の位が誤りだった場合の正しい数字の候補173594をチェックしたとき、
正しい数字「173592」を求めていたはず。つまり、
173591は、
「正しい番号173592の一の位を誤った数」でもあり、同時に
「正しい番号176591の千の位を誤った数」でもあることになります。
これに気づけば、173591はどの位が誤っているのか特定できないことが断定でるのですが…
仮にこれが作問者の意図する「布石」だとすると、残念ながら受験生がその意図に気づくことは難しいでしょう。なぜならば、
「判断できる」を選ぶ場合 …すべての場合を証明することが必要。
という論理がわかっていることが前提になってしまうからです。
したがって本問で差が付く可能性はないと考えて差し支えありません。
さて、上述の「布石」に気づけなかったとしても、
この「論理」がわかれば、攻め手が見えてくるかも知れません。
ここでは「判断できない」を導くための反例を自力で探してみましょう。
計算しやすい具体例を考えていきます。
00000□の場合、□＝0より、正しい番号000000が得られます。
00001□の場合、□＝9より、正しい番号000019が得られます。
この2つの正しい番号をよく見てください。お互い1桁ずつ変えることで、
000010や000009などの「間違った」番号を作ることができます。
つまり、これらの「間違った番号」は、複数の正しい番号に対応しているため、誤りのある位を一つに特定できないことになります。何とか正解にたどりつきました。
計算しやすい具体例を考えることがポイントです。
本問で求められる力は一言で言うと「対応力」ですが、
①ルールを正確に読み取る力(読解力)
②ルールを運用する力（余りの計算に対する習熟度）
③やるべき作業を決定する力
と複合的な要素があるため、その分難度が高くなっています。
（３）で（＊）の方針がすんなり立てられるようなら、合格は堅いでしょう。
(2 votes, average: 5.00 out of 5)
Loading ...
渋谷中入試対策・関連記事一覧
渋谷中入試対策・同じ教科（算数）の記事
渋谷中入試対策・同じテーマ（合否を分けた一題）の記事
- 算数の合否を分けた一題（2016年度）
- 国語の合否を分けた一題（2016年度）
- 社会の合否を分けた一題（2016年度）
- 理科の合否を分けた一題（2016年度）
- 算数の合否を分けた一題（2017年度）
- 国語の合否を分けた一題（2017年度）
- 社会の合否を分けた一題（2017年度）
- 理科の合否を分けた一題（2017年度）
- 理科の合否を分けた一題（2018年度）
- 算数の合否を分けた一題（2018年度）
- 国語の合否を分けた一題（2018年度）
- 理科の合否を分けた一題（2019年度）
- 社会の合否を分けた一題（2019年度）
- 国語の合否を分けた一題（2019年度）
- 算数の合否を分けた一題（2020年度）
- 理科の合否を分けた一題（2020年度）
- 国語の合否を分けた一題（2020年度）
- 社会の合否を分けた一題（2021年度）
- 理科の合否を分けた一題（2021年度）
- 算数の合否を分けた一題（2021年度）
他校の同じ教科（算数）の記事
