算数の合否を分けた一題（2016年度）

算数の合否を分けた一題

渋谷中入試対策・算数の合否を分けた一題（2016年度）

難易度分類

［１］	（１）Ａ　　（２）Ａ　　（３）Ａ　　（４）Ａ　　（５）Ｂ　　（６）Ｂ
［２］	（１）Ｂ　　（２）Ｂ　　（３）Ｂ～Ｃ
［３］	（１）Ａ　　（２）Ａ　　（３）Ｂ
［４］	（１）Ｂ　　（２）Ｂ　　（３）Ｂ～Ｃ

A…渋谷教育学園渋谷中合格を目指すなら必ず得点したい問題
B…着眼点や解法により正答率・かかる時間に差がつく問題
C…難易度や処理量から判断して、部分点狙いで答案を作成すべき、もしくはとばすべき問題

問題別寸評

［１］

６題からなる小問集合、（６）のみ、式･考え方の記述を要求されるという例年どおりの出題です。

（１）

分数と小数が混ざった逆算タイプの計算問題です。本校の出題としては特に複雑とも言えず、確実に正解しておきたい問題です。

（２）

食塩水のやり取り算です。互いに入れ替えたら濃度が等しくなるという典型的な出題です。いくつかの解法が考えられますが、「等しくなった濃度は、ＡとＢの食塩水を全て混ぜたときの濃度に等しい」ことに注目して解くことを、まずはマスターしておきましょう。

（３）

隠れた正三角形を探し出すことがポイントです。本校受験生にとっては基本レベルと言えるでしょう。

（４）

「約数の個数がちょうど３個である整数」＝「素数の２乗」という事実は身に付いている受験生が多いでしょう。ただ、「１以上２０１６以下」とやや範囲が広めです。
４３×４３＝１８４９と４７×４７＝２２０９を確認し、その後４３までの素数の個数を数え上げる過程でミスをした受験生も多そうです。

（５）

「たての長さと横の長さの比が１：２である」「３つの長方形Ａ，Ｂ，Ｃ」とありますが、図から長方形Ｂは「たて：横＝２：１の長方形」であると思われます。問題文どおりに解釈すると解答を得ることが不可能であり、厳密には出題ミスと言わざるを得ませんが、おそらく受験生への影響は大きくなかったことでしょう。
長方形Ａのたて＝①、横＝②と比で置くことさえ出来れば、Ｂのたて：横＝２：１、Ｃのたて：横＝１：２であることやＤが正方形であることを使って辺の長さの比を順次書き込んでいくことで解決しますが、糸口である「まず比で置く」という発想に至ることが出来なかった受験生も一定数いたでしょう。

（６）

４種類の数字だけを使って出来る整数の問題ですから、４進数の考え方で解くのが簡明です。
２→０、３→１、５→２、７→３と各数字を置き換えることによって、普通の４進数に置き換えられますが、２２２２２２→００００００から始まっていることに注意が必要です。本問は、４進数で「２０１５」番目の数を求める問題と本質的に同じですが、２０１６番目を求めてしまうミスも多かったと思われます。

［２］

場合の数の出題です。サイコロの目にしたがって点を動かすという「すごろく型」のよくある設定のようですが、整理の仕方によって解答時間や正答率に大きく差が出る問題と言えます。

（１）

１～６の目に注目して、普通の樹形図を書き出すようでは、処理があまりにも大変です。本問では、奇数の目のときには１つ、偶数の目のときには２つ進むというルールですから、まずは「１」と「２」の数字だけを使って進み方を整理し、その後、目の出方としては何通りになるのかを計算するというステップを踏まないと、正答するのは困難でしょう。
Ｃに止まるまでの進み方は「１→１」または「２」。その後Ａに止まるまでの進み方も「１→１」または「２」となりますね。
「１→１」という進み方は、サイコロの目の出方としては３×３＝９通り、「２」という進み方は、サイコロの目の出方としては３通りであることを押さえた上で、あとは計算で答えを求めます。

（２）

ちょうど１周してゲームが終了するのは、（１）の場合に加えて「１→２→１」という進み方だけであることに気が付くことができれば、見通し良く解くことができます。

（３）

ちょうど２周してゲームが終了するためには、１周目にＡに止まってはいけないことに注意が必要です。さらに、１回のサイコロで１つか２つしか進めないことを考えると、
　①Ａ→Ｄまで３つ進む（途中どのように止まってもよい）。
　②Ｄ→Ｂまで２つ進む（途中のＡには止まらない）。
　③Ｂ→Ａまで３つ進む（途中どのように止まってもよい）。
と、３つのステップを踏むことになります。①・②・③がそれぞれサイコロの目の出方としては何通りになるのかを考えてみましょう。
ともあれ、合格レベルの受験生にとっても、やや厳しい設問であったかもしれません。

［３］

ここ数年は、ややとらえにくい立体図形の問題が出題されていましたが、本年は（２）までは平面図形、（３）のみが解法次第で差のつきそうな立体図形という内容の出題でした。

（１）

相似比と面積比の関係を用いる、ごく基本的な問題です。

（２）

折り返した後の点ＡがＢＣより下にくることに注意が必要ですが、本校受験生にとって難しい問題ではないでしょう。必要な長さを相似に注目して確実に求めていきましょう。

（３）

回転体の体積を求めさせる設問です。軸の上下に図形が存在するので、軸の下側の図形を上に折り返してから回転しても求める体積は変わらないことを利用するのがよいでしょう。
類題を練習したことがないと、正解するのはやや難しかったと思われます。

［４］

速さの出題です。例年通り、記述式で条件整理がやや面倒な問題が配置されました。ただ、本年は「時間」を中心に整理していくと、見かけほど複雑な計算も必要でなく、合格者の中には、むしろ簡単だと感じた受験生もいたことでしょう。合格者と不合格者の間で、大きく差のついた大問であったと思われます。
詳しくは、「合否を分けた一題」として後述します。

合否を分けた一題

大問４題、［１］が小問集合、［２］［４］に条件整理系、［３］に立体図形という形式は例年通りです。
本年は、合格レベルの受験生にとっては比較的解きやすいが、充分な演習を積んでいない受験生にとっては難しいであろうという問題が多くみられました。合格者平均点は本校としてはやや高めであると推測しますが、差のつきやすいテストであったと言えるでしょう。
合否を分けた一題として、［４］の速さの問題を取り上げます。

［４］

長い問題文に数多くの条件が記されていて、相当な難問に見えるかもしれません。このような場合には、問題文を読みながら、以下に示すような形で「時間」に注目して状況図に整理していくことが有効である場合が多くあります。

「午前９時に３人は同時にスタートし、…」から始まる段落を読んで、

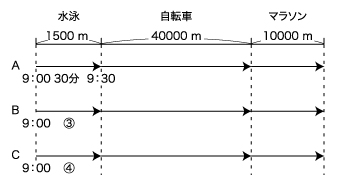
ＢさんとＣさんの泳ぐ速さの比は４：３とありますが、図には時間の比である３：４を書き込みます。

「ＡさんとＣさんの自転車で走る速さは同じでしたが、…」を読んで、

「Ａさんは、水泳にかかった時間の…」を読んで、

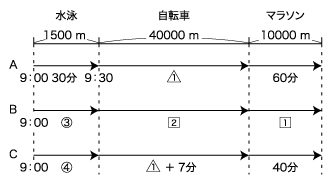
先ほどと同様、速さの比は時間の情報に直して書き込みます。

「この結果、Ｃさん、…」を読んで、

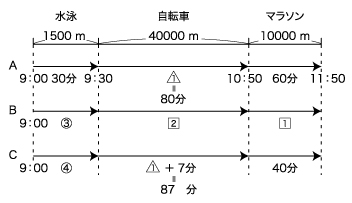
ここまでで、まず（１）を解決することが出来ます。

上で示したとおり、Ａさんについては、水泳・自転車・マラソンにかかった具体的な時間が比較的簡単に分かるようになっています。
水泳３０分→マラソン６０分→自転車８０分の順に求められることを再度確認してみてください。

４００００ｍ÷８０分＝５００ｍ／分…（１）

さらに、「Ｂさんはマラソンコースの下見をしようと思い、…」を読むと…。

Ｂさんが自転車にかかった時間とマラソンにかかった時間の比は２：１、道のりの比は４０ｋｍ：１０ｋｍ＝４：１ですから、自転車とマラソンの速さの比は（４÷２）：（１÷１）＝２：１であることが分かります。
マラソンコースを自転車で走ると２５分短縮されることになりますから、自転車とマラソンの速さの比が２：１であることより、同じコースを走るのにかかる時間の比は１：２。よって、マラソンにかかった時間は５０分と求められます。
そうすれば、Ｂさんが自転車にかかった時間も１００分であったことが分かりますね。

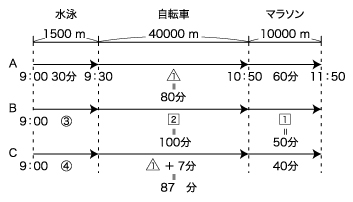
これで（２）も解決できました。
４００００ｍ÷１００分＝４００ｍ／分…（２）

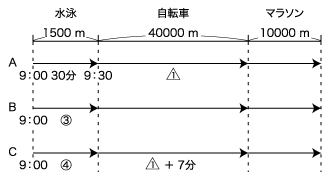
ここまでの整理によって、Ａさんがゴールまでにかかった時間は１７０分、Ｂさんは③＋１５０分、Ｃさんは④＋１２７分と表せています。
さらに、Ｃさん、Ａさん、Ｂさんの順にゴールし、ＣさんとＡさんの時間の差とＡさんとＢさんの時間の差が同じであることから、Ａさんの時間はＢさんとＣさんの時間の平均になっているととらえると分かりやすいでしょう。

（Ｂさんの時間）＋（Ｃさんの時間）＝（Ａさんの時間）×２
ということになるので、

⑦＋２７７分＝３４０分
⑦　　　　　＝　６３分
④　　　　　＝　３６分

と順に求められ、Ｃさんがゴールまでにかかった時間は、１２７＋３６＝１６３分。よって、（３）の答えは１１時４３分と求められました。

著者：桑田陽一

この記事は役にたちましたか？