算数の合否を分けた一題
芝中学入試対策・算数の合否を分けた一題(2020年度)
難易度分類
| 大問1 | (1)A (2)A |
|---|---|
| 大問2 | (1)A (2)A |
| 大問3 | A |
| 大問4 | A |
| 大問5 | B |
| 大問6 | 金額:B 個数:B |
| 大問7 | (1)B (2)C |
| 大問8 | (1)A (2)A |
| 大問9 | (1)A (2)B |
| 大問10 | A、A、B |
A・・・芝中合格を目指すなら、確実に正解したい問題
B・・・知識、解法次第で、得点に大きく差がつく問題 ⇒ 合否を分けた問題
C・・・難易度、処理量から判断して、正解できなくても合否に影響しない問題
問題別寸評
(1)四則演算
一般的な四則演算です。確実に正解しましょう。
(2)四則演算の逆算
一般的な四則演算の逆算です。確実に正解しましょう。
大問2 倍数
(1)
小さい数字から順に書き出していけばすぐに答えが出ます。確実に正解しましょう。
(2)
(1)で求めた数字と、5で割ると1余る数を書き出して共通する最小の数字を見つけましょう。その数に、3と7と5の公倍数である105を足していきます。丁寧に取り組めば解ける問題でした。
組み合わせが循環しているタイプの消去算では、表を活用して解きます。
アイスクリームの値段を安い順にA、B、C、D、Eとすると、下の表のようになります。
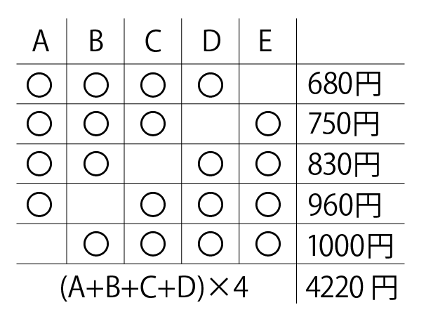
上の表より、A+B+C+D+E=1055円と分かりますので、3番目に高いアイスクリームCは
1055-830=225より、225円と分かります。
類題を解いたことがあると解きやすかったと思われます。
まず、この問題のように非常に大きい数字の時は必ず規則性があるということを意識しましょう。
少し書き出してみると、次のようになります。
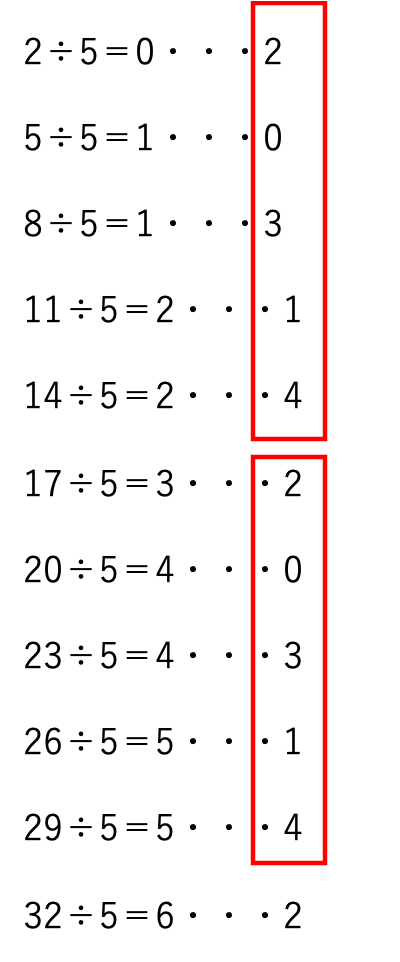
このように、2、0、3、1、4の5つの数がずっと続きます。
2019÷5=403・・・4より、403×(0+3+1+4+2)=4030
周期の4番目までの和は、2+0+3+1=6なので、4030+6=4036と求まります。
場合の数と立体図形の複合問題は珍しいですが、冷静に考えれば対処できたでしょう。
三角柱の高さの各辺が4等分されているので、高さをC(=F=I)=1、B(=E=H)=2、A(=D=G)=3、それぞれの辺の一番上の頂点を4とすると、3つの辺の高さの合計が(4×3÷2=)6になれば、その3つの点を通る平面で三角柱を切った時にできる2つの立体の体積が等しくなると言えるので、切り方は以下のようになります。
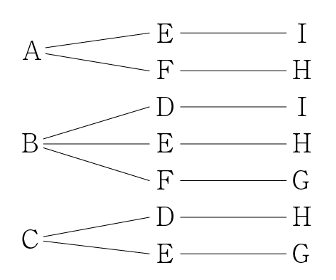
上記より7通りと分かります。

(1)
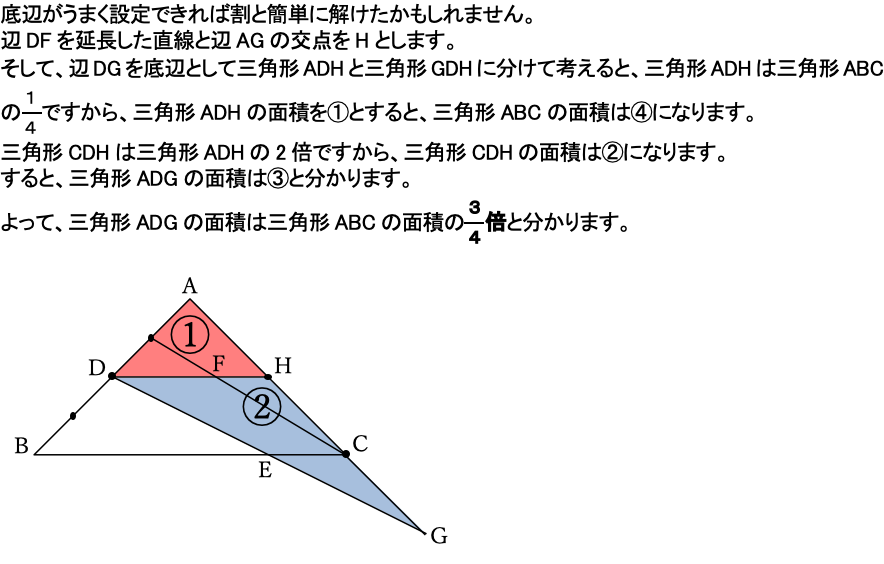
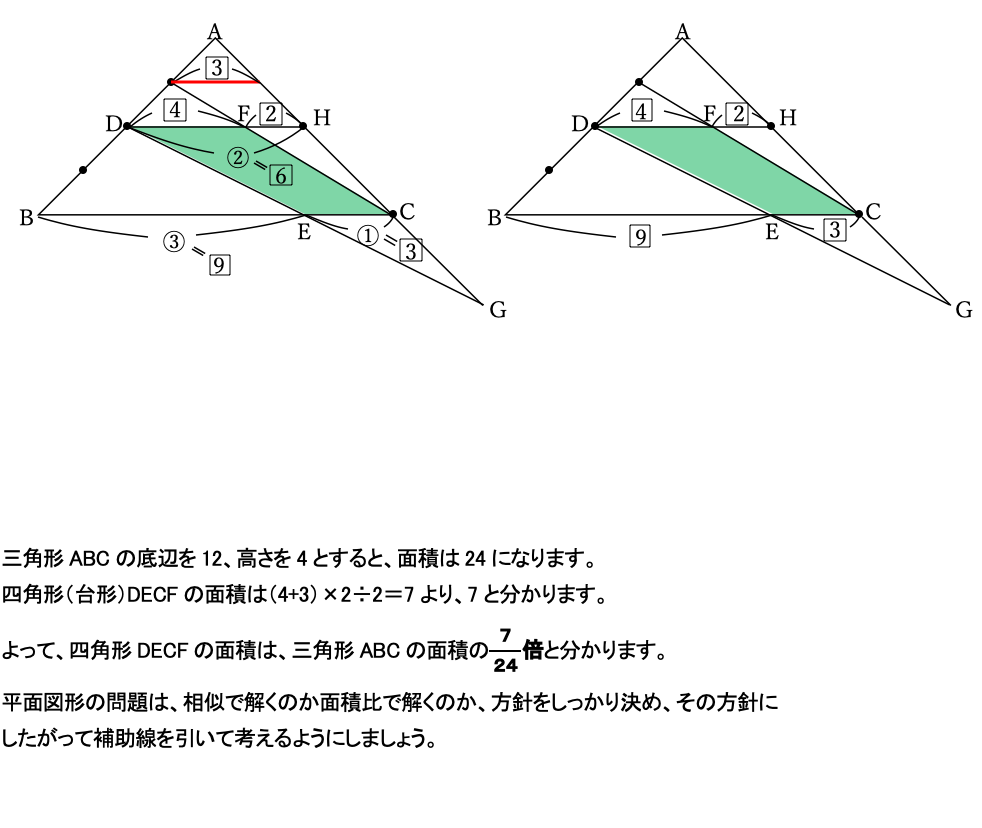
(2)補助線が引けないと、答えにたどり着くのが厳しかったと思います。
この問題ではDFとECがどれくらいの長さになるのかが分かれば解けるので、それぞれを求めるために、以下の青で塗った三角形と赤で塗った三角形に着目します。
すると以下のようになります。

次にこれらを比合わせしていきます。
すると以下のようになります。
比合わせしたものを整理すると右下のようになります。
(1)一般的な仕事算です。計算ミスをしないようにしましょう。
(2)仕事算とつるかめ算の複合問題です。難易度は高くないので確実に正解しましょう。
合否を分けた一題で取り上げます。

合否を分けた一題
大問9は、(1)で求めた答えが(2)に直結するということに気づくことができた受験生は一瞬で解けたかもしれません。逆に気づくことができなかった受験生は、何をすればいいか皆目見当がつかなかったと思います。そのため明確に解答時間及び正解率が分かれたと思いますので、この問題を今年の合否を分けた一題とさせていただきました。
(1)正方形を3等分する点に着目できれば容易に正解できるでしょう。
下の図より、6×8-(2×6÷2+4×8÷2+2×6÷2)=20
よって、3点イ、エ、ケを結んでできる三角形の面積は20㎠と分かります。

(2)半径の分からない円の面積を求めるにはどうしたらいいかというポイントに気付くことができれば一瞬で解けたかもしれません。
点ア~点クは円を8等分する点なので、角イケエは90度だと分かります。
また、辺イケと辺エケは円の半径ですので、三角形イケエは直角二等辺三角形だと分かります。
(1)で三角形イエケの面積は20㎠と分かっているので、イケ×エケ(=半径×半径)=40です。
よって、点ア~点クを通る円の面積は40×3.14=125.6より、125.6㎠と分かります。

総評
今年の受験者平均は54.2点、合格者平均は67.1点とほぼ例年通りでした。
大問数、小問数ともに例年から少し増えました。
今年の問題は、“気付き”を要する問題が多かった印象です。
ただ、大問7の(2)以外の問題は典型題が完璧にできる状態になっていれば、十分対応できる難易度でした。
芝中に合格するためには難しい問題を演習する必要は一切なく、標準レベルまでの典型題を完璧にすることが大切と言えますので、標準レベルまでの典型題で解けない問題をなくしましょう。
芝中学入試対策・関連記事一覧
芝中学入試対策・同じ教科(算数)の記事
芝中学入試対策・同じテーマ(合否を分けた一題)の記事
- 算数の合否を分けた一題(2016年度)
- 国語の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2016年度)
- 理科の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2017年度)
- 国語の合否を分けた一題(2017年度)
- 社会の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2018年度)
- 国語の合否を分けた一題(2018年度)
- 理科の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2019年度)
- 国語の合否を分けた一題(2019年度)
- 国語の合否を分けた一題(2020年度)
- 理科の合否を分けた一題(2020年度)
- 社会の合否を分けた一題(2020年度)
他校の同じ教科(算数)の記事
記事はいまのところありません。






