算数の合否を分けた一題
芝中学入試対策・算数の合否を分けた一題(2019年度)
難易度分類
| 1 | (1)A (2)A |
|---|---|
| 2 | B |
| 3 | (1)A (2)A |
| 4 | (1)B (2)B |
| 5 | A |
| 6 | (1)A (2)B |
| 7 | C |
| 8 | (1)A (2)C |
| 9 | B |
A・・・芝中学を目指すなら確実に正解したい問題
B・・・解法によって、得点、解答時間に差がつく問題
C・・・難易度、処理量などから失点もやむない問題
出題総評
大問数9、小問数15、解答形式などに変更はなく、傾向は例年と変わっていません。
大問1~5までは典型題が並び大きく差がつくことはなかったと考えられます。
大問6以降に一見難しそうな問題が並んでいますが、決して難しすぎるということはありません。
前半での失点を抑え、後半の問題である程度得点できれば十分合格点に到達します。
解答用紙への式の記入などは求められていないため、ミスなく正確に問題を解く必要があります。計算の速さと正確性を高める訓練は必須です。
問題別寸評
計算問題は例年2問程度の出題があり、今年は2題でした。
「小数と分数の四則演算」です。日頃から小数から分数、場合によっては分数から小数への変換をスムーズに行うことが出来るよう、計算練習を行いましょう。
確実に正解したい1問です。
「逆算」の問題です。-□、÷□の逆算となり、計算順序を間違えやすいです。
こちらも確実に正解したい1問です。
「差集め算」の問題です。8冊ずつ配ったときと、男の子に9冊ずつ、女の子に7冊ずつ配ったときの差に着目して問題を解きます。
5冊足りなかったノートが4冊余るので、全体の差は9冊です。
男の子よりも女の子が1人多くなると1冊余りますので、女の子は男の子に比べ9÷1=9人多いことがわかります。
「周期算」の問題です。また、(2)を解くための誘導問題です。
落ち着いて計算を行いましょう。
(1)より、周期は4ですから、2019を4で割ってあまりを調べます。
「数の性質」の問題です。
奇数+偶数は必ず奇数に、奇数+奇数は必ず偶数になることから、64,54,46の数字に着目して問題を解きます。
「数の性質」の問題です。
(1)で求めた答えを利用して、3つの偶数と1つの奇数を求めます。
「平面図形」の問題です。平行線に着目し角BDEを求め、折り返す前の状態を考えます。アの大きさ2つ分と62°を合わせると180°になることから、アの角度の大きさを求めます。
「平面図形」の問題です。分割して問題を解きます。
台形を24分割し、三角形ABCが全体のいくつ分になるのかを考えます。
確実に正解したい1問です。
(1)で作図した24分割の図を使って、影の部分が全体のいくつ分かを考えましょう。
「食塩水の濃さ」の問題です。
それぞれの容器から等しい量の食塩水を取り出し入れ替えたあと、それぞれの容器に入っている食塩の重さの比に着目して問題を解きます。
食塩水を入れ替える前と後では食塩の重さの合計は変わりません。
まずは容器Aと容器Bに入っている食塩の重さを求めましょう。
容器Aに入っている食塩は800×0.06=48g、容器Bに入っている食塩は600×0.12=72gですので、食塩の重さの合計は48+72=120gです。
食塩水を入れ替えたあとの容器Aと容器Bに入っている食塩水の重さの比は、800:600=4:3で、濃さの比は9:8ですから、食塩の重さの比は(4×9):(3×8)=3:2です。
比の和の5が120gですから、1が24gと決まり、食塩水を入れ替えたあとAの容器に含まれる食塩は24×3=72gです。この後の解法は様々ですが、100gごとに6gずつ容器Aの食塩が増えますので、(72-48)÷6=4、よって400gとなります。
「規則性」の問題です。
1~21までの数字に何色が塗られるかを書き込みましょう。すると、3列目に並べられたカードは黄、青、赤、白・・・の周期4で並ぶことに気付きます。3列目で初めて白色になる数字は24、その後7×4=28の公差で52、80、108、136、164、192と裏が白のカードが並びます。よって、その和は(24+192)×7÷2=756です。
確実に正解したい1問です。
(1)である程度書き出しを行っていると、1列目と5列目、2列目と6列目、3列目と7列目の数字が同じ色の組み合わせになっていることがわかります。1~200までに数字を並べると、200÷7=28…4より、28+1=29行目ま数字が並んでいることがわかります。この29行目に並ぶ197、198、199、200の4つの数字が落とし穴となっておりいずれも裏に塗られた色が異なります。その点を注意し、1~200までの数字の和から4列目に並ぶ数字と197、198、19の3つの数字を引いて答えを求めます。
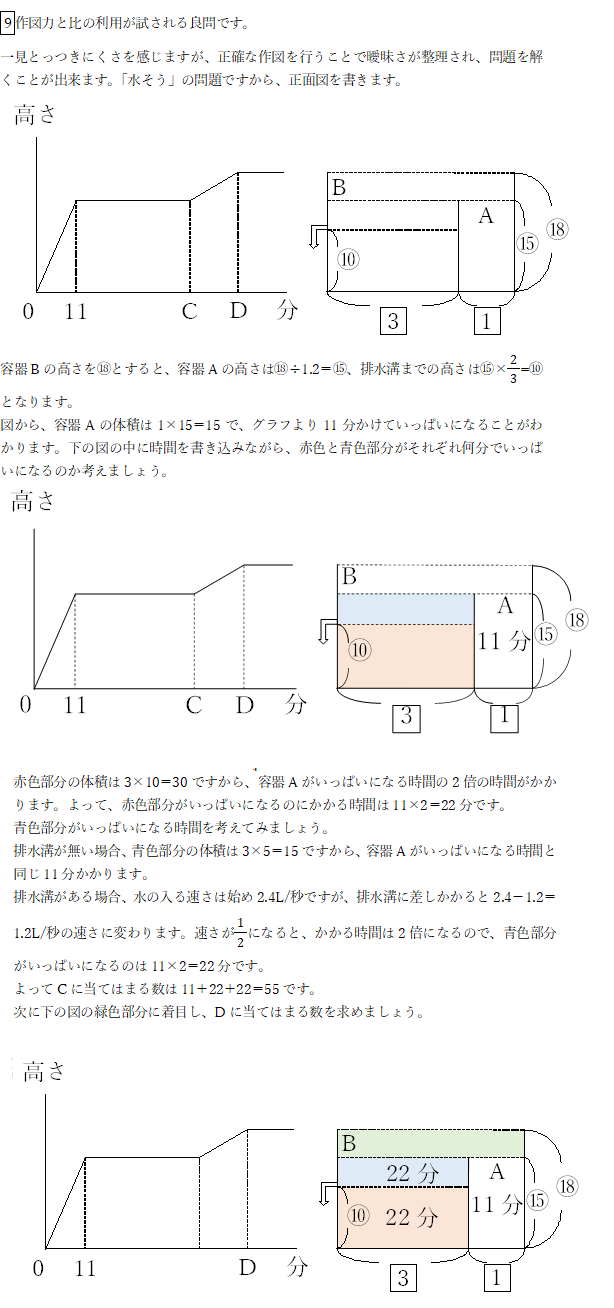
「水そう」の問題です。
作図して問題を解きます。合否を分けた一題で解説を行います。
合否を分けた一題
先ほどと同様に、緑色部分をいっぱいにするのにかかる時間を求めましょう。
緑色部分の体積は、4×3=12ですから、排水溝が無い場合、15:11=12:□を解いて8.8分かかることがわかります。
排水溝がある場合、2倍の時間がかかるので緑色部分は8.8×2=17.6分でいっぱいになります。
よって、Dに当てはまる数は55+17.6=72.6です。
このように、正確な作図を用意し、水が溜まっていく様子をつかみながら、比を用いてCとDに当てはまる数を求めることできます。
問題文の図を眺めながら頭でイメージして解ききることは難しいので、愚直に正面図を描くことを怠らなかったお子さんに軍配が上がった問題でした。
芝中学入試対策・関連記事一覧
芝中学入試対策・同じ教科(算数)の記事
芝中学入試対策・同じテーマ(合否を分けた一題)の記事
- 算数の合否を分けた一題(2016年度)
- 国語の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2016年度)
- 理科の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2017年度)
- 国語の合否を分けた一題(2017年度)
- 社会の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2018年度)
- 国語の合否を分けた一題(2018年度)
- 理科の合否を分けた一題(2019年度)
- 国語の合否を分けた一題(2019年度)
- 国語の合否を分けた一題(2020年度)
- 理科の合否を分けた一題(2020年度)
- 社会の合否を分けた一題(2020年度)
- 算数の合否を分けた一題(2020年度)
他校の同じ教科(算数)の記事
記事はいまのところありません。