算数の合否を分けた一題（2018年度）

算数の合否を分けた一題

芝中学入試対策・算数の合否を分けた一題（2018年度）

難易度分類

［１］	(1)A　(2)A
［２］	B
［３］	A
［４］	A
［５］	(1)A　(2)B
［６］	A
［７］	(1)A　(2)A　(3)A
［８］	(1)B　(2)C
［９］	B

Ａ：芝合格を目指すなら必ず得点したい問題
Ｂ：着眼点や解法ツールにより正答率・かかる時間に差がつく問題
Ｃ：難易度や処理量から判断してとばすべき問題

出題総評

今年も、大問１は計算問題が全２問、大問２～９は様々な単元にわかれての中問集合、という昨今の形式が踏襲された入試となりました。
詳細については、大問１が分数や小数の混合計算および逆算、大問２は平均算、大問３は割合（食塩水）、大問４は割合（倍数算）、大問５は数の性質の問題、大問６は平面図形の問題、大問７は速さの文章題、大問８は規則性の問題、大問９は立体図形の問題でした。

問題別寸評

［１］

(1)

答　４．２
分数と小数が入り混じった計算問題。落ち着いて一つずつ順番に計算し、答えを出すように。

(2)

答　４．８
分数と小数が入り混じった逆算の問題。先に計算できるところは、計算をして数値をしっかりと求めておくように。(1)も含め、ここでの失点は避けたいところです。大問１で費やせる時間は４分程度まででしょう。

［２］

答　１５．７５ｇ
１０個の重さの平均を求める問題。計算の工夫が出来そうですが、あれこれ考えると時間を浪費するだけです。率直に、全ての値の合計を取って１０で割ってしまいましょう。ただ、縦に１０個の数値をとって筆算するのは計算ミスを誘発するだけなので、２つずつの和を取って少しずつ計算していく方が望ましいです。

［３］

答　８％
２種類の食塩水の、典型的なやり取りの問題。流れ図（分子に塩の量、分母に全体量を記した分数の図）を用いて、動きを整理していくようにしましょう。以下のようになります。

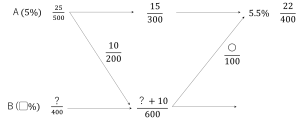
上図より、〇は２２－１５＝７となり、７×６＝４２が？＋１０なので？＝３２、Ｂの最初の濃度が求まります。

［４］

答　Ｂ君…１２００円　買ったもの…４００円
登場人物が３人いる倍数算の問題。各々の人物の状態を、問題文の条件と照らし合わせながら式にしていきましょう。Ｃ君の残金を①円とおくと、Ｂ君の残金は②－２００円となり、さらにＡ君の残金は（②－２００）×３＋７００＝⑥＋１００円となります。
Ａ　３５００－買ったもの　＝　⑥＋１００
Ｂ　　　□　－買ったもの　＝　②－２００
Ｃ　　９００－買ったもの　＝　①
３人が買ったものはみな同じ額なので、それぞれの金額の差が買う前と後で変わらないことに着目します。ＡとＣの差を見てみると、２６００＝⑤＋１００となるので、①＝５００となって答えが求まります。

［５］

“…で…回割れる”という考え方を基にした数の性質の問題。詳細は、合否を分けた一題として後述いたします。

(1)

答　４個

(2)

答　７回

［６］

答　１２．５倍
正三角形をテーマとした、面積比の問題。ＥＧＣＦが四角形なので、点Ｆから点Ｇに直線を引いて２つの三角形にわけます。△ＦＧＣは１辺が１ｃｍの正三角形、△ＡＢＣは１辺が５ｃｍの正三角形なので面積比が求まります。また、△ＥＦＧも△ＦＧＣも面積が同じことからも答えが導き出せます。平易な問題なので、確実に得点しなければなりません。

［７］

特殊算の考え方が絡む、速さの問題。時間、分の単位に気を付けてさえいれば易しい問題です。確実に全て得点しましょう。

(1)

答　３６㎞
時速２０㎞で進んだ時間と時速８０㎞で進んだ時間の合計が与えられており、全体の距離も与えられています。速さが２種類あり、各々の時間を考えていくので鶴亀算です。一般道でかかった時間が１．８時間とわかり、答えが出せます。

(2)

答　時速８８㎞
(1)より高速道路は３００－３６＝２６４㎞、問題文の条件から高速道路で費やした時間が５時間６分－１８分－１時間４８分＝３時間となるので速さが求まります。

(3)

答　２０８㎞
一般道でかかる時間はこれまでと変わらず１時間４８分なので、高速道路でかかった時間は５時間２０分－１時間４８分＝３時間３２分です。距離が２６４㎞で、時速８０㎞および時速６０㎞と２種類の速さが存在するので、(1)と同様に鶴亀算を用いれば答えが出ます。

［８］

数表が絡む、規則性の問題。１列の奇数行と、７列の偶数行が空欄になっていることに注意を払わなければいけません。

(1)

答　８４行の５列目
１から１２までを１グループとして考えます。５００÷１２＝４１…８ですが、あまりが８ということは１つの行につき数が６個までなので２行目に差し掛かります。１グループにつき２行なので、２×４１＝８２行に先ほどの２行を追加することに注意しましょう。

(2)

答　６６０４
全体を通じて、丁寧な規則の書き出しや緻密な作業力、計算力が求められる難問でした。５列目の数について、１・２行目の和は１２＝１２×１、３・４行目の和は３６＝１２×３、５・６行目の和は６０＝１２×５となり、１２×（手前の行数）となることが言えます。したがって、２１・２２行目の和は１２×２１＝２５２となり、問題で問われていることから４９・５０行目の和は１２×４９＝５８８。２５２＋２７６＋…＋５８８となるので、等差数列の和の公式を使って求めます。また、５１行目については５１・５２行目の和が１２×５１＝６１２、５１行目の数と５２行目の数の差は４なので和差算を使って求めます。あとは、両者を合計すれば答えが求まります。２行ずつの和を取って規則を見つけ出さなければならないことに加え、中途半端な５１行目についても考えなくてはいけないことを考えると、試験全体で最も難しい問題だったと言えるでしょう。

［９］

答　ＤＥ…１．５cm　点Ｄを含む立体の体積…１７．６２５㎤
昨今の入試で、どの学校でも出題されやすくなっている立体切断の典型題。線を延長して考えるという方法はしっかりと身に着けておきましょう。まずは、ＣからＢの線を延長すると下図のようになります。

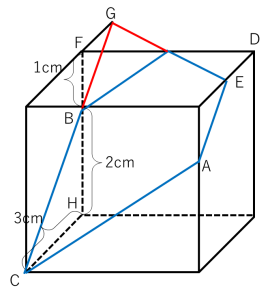
ＦＢＧとＨＣＢの砂時計相似に着目すると、ＦＢ：ＢＨ＝ＦＧ：ＨＣ＝１：２なので、ＦＧは３÷２＝１．５cmとわかります。同様に、ＣからＡの線を延長すると下図のようになります。

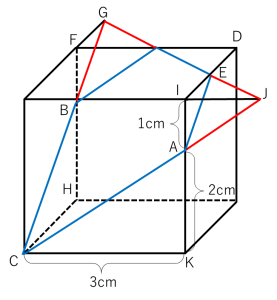
ＩＪＡとＫＣＡの砂時計相似に着目すると、ＩＡ：ＡＫ＝ＩＪ：ＫＣ＝１：２なので、ＩＪは３÷２＝１．５cmとわかります。

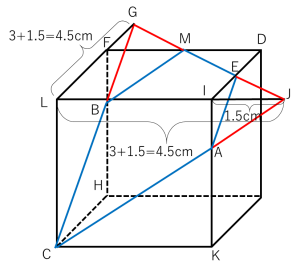
上図より、ＧＪＬとＥＩＪがピラミッド型相似となり、ＧＬ：ＪＬ＝４．５：４．５＝１：１となるので、ＩＥの長さが求まり、そこからＤＥの長さも求まります。
点Ｄを含む立体については、含まない方を求めて全体の３×３×３＝２７㎤から引いて考えます。含まない方については、底面を△ＧＪＬ、高さをＬＣとする三角錐から底面を△ＥＩＪ、高さをＩＡとする三角錐を２つ（底面を△ＧＦＭとする方も同じ三角錐です）引けば求まります。計算が複雑になるので、まずは立式をしてから約分するべきところはして簡単にしてから計算をするように。

合否を分けた一題

今回は、中盤の問題群の中で数の性質の単元である大問５について合否をわけた一題として紹介しましょう。“…で…回割れる”という考え方は、単元内において定石の考え方ですが、本問ではその考え方に少しの捻りがあり、多くの受験生を悩ませた問題と言えるでしょう。

［５］数の性質

(1)

一の位から０が～個並ぶ＝その数が１０で～回割れる⇒１０＝２×５なので、５で～回割れる？ということになります（２の方が５よりも出てくる回数が多く、２は余ってしまい１０になることが出来ない）。
問題の１８から３０までの５の倍数を拾います。２０・３０はそれぞれ５で１回割れるが、２５は５で２回割れます（２５＝５×５）。したがって、１＋１＋２＝４回割れるので、４個となります。
答え：４個

(2)

４＝２×２なので、２００６から２０１８までの２の倍数を調べていきます。２で２回以上割れるもの（２×２＝４の倍数や２×２×２＝８の倍数など）もあるので、数を２×□の形にして考えていきます。なお、奇数は２で割れないので調べる必要はなく、対象は２００６・２００８・２０１０・２０１２・２０１４・２０１６・２０１８となります。
２００６＝２×１００３
２００８＝２×２×２×２５１
２０１０＝２×１００５
２０１２＝２×２×５０３
２０１４＝２×１００７
２０１６＝２×２×２×２×２×６３
２０１８＝２×１００９
合計すると２が１４個となりますが、４は２が２個必要なので、１４÷２＝７回となります。
答え：７回