理科の合否を分けた一題
芝中学入試対策・理科の合否を分けた一題(2018年度)
難易度分類
| 1 | (1) A (2) B (3) A (4) A (5) A (6) A (7) A (8) A |
|---|---|
| 2 | (1) A (2) A (3) B |
| 3 | (1) A (2) A (3) B (4) C (5) B (6) C |
| 4 | (1) A (2) A (3) A (4) A (5) A (6) B(7) C |
| 5 | (1) A (2) A (3) B (4) B |
| 6 | 問1(1) A (2) A (3) A 問2(1) A (2) A (3) A (4) A |
A…芝合格を目指すなら、確実に得点したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難易度、処理量から判断して、部分点を拾えればよしとする問題
出題総評
2018年度の芝は、例年通り、基本的知識を問う問題、グラフや表の読み取って数的処理を行う問題、実験を通して考察を進める問題が出されました。
40分75満点。平均点36.9点(昨年度32.0点)、合格者平均43.8点(昨年度38.6点)と、昨年よりやや上がっていますが、ここ数年の中では、昨年のついで低い数字です。
小問集合は、熱気球による調査を行う設定での問題。
物理分野の問題は、ホイートストンブリッジ回路のバリエーションと、針金につけたおもりの重心をもとめる問題。
化学分野の問題は、炭酸水素カルシウムの加熱分解・中和反応の問題。
生物分野の問題は、「方形区法」によって、草むらの植物を調べる問題。
地学分野の問題は、星座や月の見え方について考える問題。
基本知識と難問とのメリハリがはっきりしています。
基本知識はまんべんなくおさえておき、得点できるところでしっかり得点する必要があります。
本年の物理分野の重心をもとめる問題のように、骨がある問題は後回しにし、標準的だった生物や地学の問題を優先して取り組むとよいでしょう。
基本の知識はもちろんのこと、根本原理をしっかりおさえた上で、データ処理を的確に行い、算数の手法を自在に活用する力をつけておきましょう。
問題構成は、4分野から大問6題、小問43問。
解答形式は、数字が21問、記号選択が17問、言語が4問、記述が1問。作図はありませんでした。
数字は、浮力・データ処理・図形の考え方を使って解くものでした。
選択肢は、比較的選びやすいものが多くみられました。
言語は、だれもが耳にしたことがある重要な語句ばかりでした。
記述は、1行程度で、典型的な内容でした。
難易度・作業量を考えると、難易度の高い計算問題を後回しにするなどの、時間配分の工夫が必要です。
問題別寸評
(総合)熱気球による調査を行う設定の問題。
芝太郎先生が熱気球に乗って、調査を終えて帰ってくるという設定です。
熱気球のしくみから、上昇して見られる景色にもふれ、広範囲で総合的な設問になっています。基本の知識を聞く問題が中心です。
(1)
温度と空気1L当たりの重さとの関係のグラフを読み取り、気球内と気球外の空気の温度差を考えます。
近い値を選択肢から選びます。
(2)
気球にはたらく浮力を計算する問題です。
誘導の文章が詳しいので、根本的な理解があれば、対応できます。
「気球にはたらく浮力」=「気球と同じ体積の外の空気の重さ」-「気球内の空気の重さ」
=(1.2-0.7)×560×1000=280000(g)=280(kg)
「気球の荷物の重さ」が「気球にはたらく浮力」より小さければ、気球は浮き上がります。
(3)
クモは、バルーニングによって、遠くまで飛ぶことができます。航空機や沖合の船にクモの糸が引っかかることもあるようです。
風に乗って飛ばすには、ツバキやアサガオの種子は大きすぎます。リンゴは偽果を捕食する動物によって運ばれ、ホウセンカは熟すると種子がはじけ飛びますが、クモやタンポポのように風にのって飛ぶことはありません。
(4)
ツバメは夏鳥で、南の国から日本に渡ってきて、春から夏にかけて産卵・子育てをします。
夏鳥にはほかに、オオルリやキビタキがいます。
(5)
川が曲がりくねっているようすを、「蛇行(だこう)」といいます。
ヘビのように曲がりくねっているという意味です。
(6)
河口のところに、土砂が堆積してできる地形ですから、「三角州」です。
「扇の形」とあるので、反射的に扇状地と答えてしまわないように注意が必要です。
(7)
過酸化水素水を酸素と水に分解するときに用いる二酸化マンガンも、「しょくばい」のひとつです。
(8)
オゾン(O3)と酸素(O2)は、どちらも酸素原子(O)からできています。
同様に、ダイヤモンドは、炭素原子が正四面体格子状に並んだ構造で、黒鉛(グラファイトともいう)は、炭素原子が平面六方格子状に配置した構造が何層にも重なっています。どちらも炭素(C)だけからできています。
このような物質同士の関係を、同素体といいます。
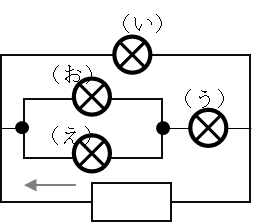
(物理)ホイートストンブリッジ回路のバリエーションの問題です。
図1は、ホイートストンブリッジ回路といわれるもので、豆電球5つが上下左右対称な形につながっています。
つなぎ方を変えたパターンでは、わかりやすく回路図を書き直して、電流の流れを把握することで、解くことができます。
(1)
図1の回路では、対称な形から考えて、点Bと点Dの電位が同じになり、BD間には電流が流れません。
したがって、豆電球(お)は点灯せず、(あ)~(え)は同じ明るさで点灯します。
(2)
(あ)を取り外したときの回路図は、下図のようになります。
豆電球に流れる電流の大きさは、
(え)>(う)>(い)=(お)
となります。
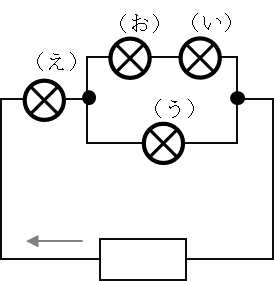
(3)
図3の回路図は、下図のように表すことができます。
豆電球に流れる電流の大きさは、
(い)>(う)>(え)=(お)
となります。
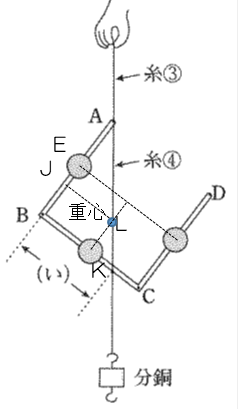
(物理)針金につけたおもりの重心をもとめるに関する問題。
針金の重さを考えないので、おもりの位置の3か所にそれぞれ重力がかかっていると考えます。
これらをまとめて1か所におきかえることができる位置が、重心です。
まっすぐな針金は重心が中央にありますが、L字型やコの字型は中央ではありません。
三角形の相似比の手法を使って、長さを計算します。
(4)~(6)は、正答率がかなり低かったのではないでしょうか。解法がすぐに思いつかない場合は、後回しにする方がよいでしょう。
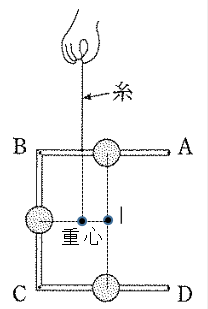
(1)
まっすぐな針金の重心は、中央にあります。
おもり3つ分の重さを、棒の両端のA・Dで支えるので、Aにかかる力は、42×3÷2=63(g)
(2)
おもり2個分の重さは、B・Dに均等にかかります。Aの真下のおもりの重さは、A点だけにかかります。
ばねはかりにかかる力は、42×2÷2+42=84(g)
(3)
Cにおもり2個分、Bにおもり1個分の重さがかかっていると考えると、逆比から、
(Bから糸までの距離):(糸からCまでの距離)=2:1
60×2/3=40(㎜)
(4)
ABの間のおもりの位置をE,糸②とBCが交わる点をF,AFとCEが交わる点をG、図7の糸の位置をHとします。
図7から、HGとBCは平行で、三角形EHGと三角形EBCは相似です。 BH:HE=1:2なので、HG:BC=2:3。したがって、HG=BC×2/3=60×2/3=40(㎜)
また、三角形AHGと三角形ABF は相似です。
AH:HB=5:1なので、HG:BF=5:6より、BF=HG×6/5=40×6/5=48(㎜)
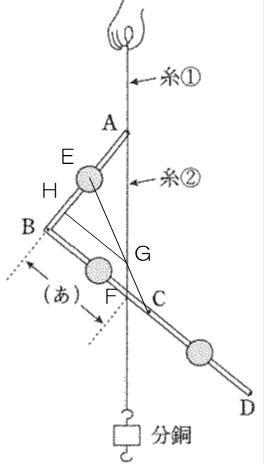
(5)
AB間のおもりと、CD間のおもりを1か所にまとめると、おもりとおもりの真ん中(I点)に2個分のおもりと置き換えることができます。
糸を支点とすると、(Bにかかる重さ):(Eにかかる重さ)=1:2より、
BJ:JE=2:1
BJ=30×2/3=20(㎜)
(6)
JLとBKは平行なので、三角形AJLと三角形ABKは相似となる。
AJ:JB=(3+1):2=2:1なので、JL:BK=2:3。
BK=JL×3/2=30×3/2=45(㎜)
(化学)炭酸水素カルシウムの中和反応に関する問題。
炭酸水素カルシウム(重そう)の化学反応は、分解や中和など、いくつかあるので、確認しておくとよいでしょう。
(1)
塩化コバルト紙が青色から赤色に変化すると、液体が水であると判断することができます。
基本の知識です。
(2)
石灰水が白くにごると、発生した気体は二酸化炭素であったことがわかります。
こちらも、おぼえておかなければいけない、物質を特定する方法のひとつです。
(3)
ガスバーナーの火を消すと、試験管内の気体が冷えて気体による圧力が減ります。
ガラス管の先が石灰水に入ったままだと、大気圧によって石灰水が試験管内に流れ込み、試験管が急に冷やされて割れることがあるので、危険です。
(4)
炭酸水素ナトリウムと中和反応をする、酸性の水溶液を選びます。
選択肢も、選びやすくなっています。
(5)~(7)
→合否を分けた1題参照。
(生物)「方形区法」による草むらの植物調査に関する問題。
「方形区法」は、高校の生物基礎で学ぶ方法です。優占種を求め,その種の特徴と環境条件との関係を考える手がかりとします。
(1)
本文から手がかりを見つけます。
「コスモスが花をつけている」とあるので、秋です。
(2)
オヒシバはイネ科の植物なので、単子葉類です。
双子葉類と単子葉類の、根や葉脈のちがいは、基本中の基本です。
(3)・(4)
本文を正確に読み取り、「方形区法」の手法通りに処理します。
オオバコよりも、カタバミから先に取り組んだ方が、スムースに処理できます。
カタバミは10区画のうち1区画に出現しているので、「頻度%」(D)は10。
「優占度」(E)は「被度%」と「頻度%」の平均なので、(4+10)÷2=7。
次に、オオバコを逆算します。「頻度%」と「優占度」がどちらも30なので、「被度%」を30とすると、「平均被度」=2.8×30/100=0.84で、小数第一位までとあるので、B=0.8とします。
これをCにもどすと、C=100×0.8/2.8=28.57≒29となり、「優占度」=(29+30)÷2=29.5≒30と確認できます。
最後に、2+B+3=8から、B=3とわかります。
(地学)星座や月の見え方についての問題。
きわめて標準的な問題です。
落ち着いて取り組み、しっかり得点したいところです。
問1(1)
北極星を見つけるには、北斗七星を利用する方法と、カシオペヤ座を利用する方法があります。
問1(2)
夕方(午後6時ごろ)見える月は、三日月~上弦の月~満月です。2時間後の午後8時ごろに「地平線近く」に見えるのは、西の方向に沈もうとする三日月があてはまります。
少し迷った生徒もいたかもしれませんが、落ち着いて考えれば解答できます。
問1(3)
北極星は、地軸の延長上にあるので、北極点では常に天頂付近に見えます。
北極点は、北緯90度の地点です。
問2(1)
北天の星座は、北極星を中心に、反時計回りに動いて見えます。
次の日の同じ時刻には、約1度動いて見えます。
問2(2)
24時間で約360度動いて見えるので、3時間で約45度(360×3/24)回転します。
問2(3)
北斗七星は、1年間で約360度動いて見えます。図の北斗七星は、反時計回りに135度動いているので、4.5ケ月後(12×135/360)とわかります。
問2(4)
天体の日周運動は、地球の自転によるものです。
また、天体の年周運動は、地球の公転によるものです。
合否を分けた1題
芝の理科は、毎年解法に悩む問題が出され、受験生を苦しめます。
本年の苦戦問題は、間違いなく大問3の(4)~(6)だったはずですが、合否を分けたとは言い難いのではないでしょうか。
むしろ、根本原理をしっかりおさえ、確実にデータを処理することが正答につながる大問4の(5)~(7)こそ、合否を分けたと考えます。
(5)
塩酸と炭酸水素ナトリウムが中和反応すると、食塩・水・二酸化炭素ができます。
(二酸化炭素の発生量)=(塩酸20g)+(加えた炭酸水素ナトリウム)-(ビーカー内に残った物質の重さ)
となります。したがって、
各ビーカーで発生する二酸化炭素の量は、下の表のようになります。
| ビーカー | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| 炭酸水素ナトリウム(g) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| ビーカー内の物質の重さ(g) | 20.0 | 20.6 | 21.2 | 21.8 | 22.6 | 23.6 | 24.6 |
| 発生した二酸化炭素の量(g) | 0 | 0.4 | 0.8 | 1.2 | 1.4 | 1.4 | 1.4 |
A~Dまでは塩酸があまり、E~Gでは炭酸水素ナトリウムがあまっていることになります。
(6)
E~Gで、発生する二酸化炭素の量が1.4gで一定になっていることから、塩酸20gがすべて反応すると、二酸化炭素が1.4g発生することがわかります。
このとき、過不足なく反応する炭酸水素ナトリウムの量は、1×1.4÷0.4=3.5(g)
(7)
濃さが1.5倍で、実験Ⅱと同じ20g使うので、塩酸にとけている塩化水素の量は、1.5倍になります。
過不足なく反応する炭酸水素ナトリウムの量も1.5倍になるので、3.5×1.5=5.25(g)。
このとき発生する二酸化炭素の量も1.5倍になるので、1.4×1.5=2.1(g)。
以上から、下の表のようになります。
| ビーカー | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| 炭酸水素ナトリウム(g) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 発生した二酸化炭素の量(g) | 0 | 0.4 | 0.8 | 1.2 | 1.6 | 2.0 | 2.1 |
A~Fまでは塩酸があまり、Gでは炭酸水素ナトリウムがあまっていることになります。
芝中学入試対策・関連記事一覧
芝中学入試対策・同じ教科(理科)の記事
他校の同じ教科(理科)の記事
記事はいまのところありません。