算数の合否を分けた一題（2021年度）

問題別寸評

(1)

分数・小数を含んだ計算問題です。確実に正解しなければなりません。

(2)

　1けたの数は何個、2けたの数は何個、3けたの数は…と考えていく「ケタばらし」の問題です。聖光学院受験者であれば確実に“見たことある”典型題ですので、やはり確実に正解したい1問でした。

(1)

3種類のつるかめ算（3段つるかめ算）の問題です。
　2種類のいもづる算（不定方程式）で処理し、条件の「お母さんのケーキは他の9人のものとは違う種類」になるような組み合わせだけ考えます。
　確実に得点したい問題でした。

　4けたのMとして考えられるのは1000以上です。
また、「4倍すると（4けたの）Nになる」ので、Mの最大は
　9999÷4＝2499あまり3
より、2499とわかります。
　よって、Mは1000以上2499以下の
　2499－1000＋1＝1500（個）
考えられます。
　確実に正解したい1問です。

(2)

「Mを4倍するとNになる」
「Mの千の位とNの百の位は等しく、また、Mの百の位とNの千の位は等しい」
という2つの条件を満たすMの上2けた（千の位と百の位）を考えます。
Mの上2けたが「10」のとき、Mを4倍したNの上2けたが「01」になることはありません。
Mの上2けたが「11」のとき、Mを4倍したNの上2けたが「11」になることはありません。
Mの上2けたが「12」のとき、Mを4倍したNの上2けたが「21」になることはありません。
このように調べていくと
Mの上2けたが「17」のとき、Mを4倍したNの上2けたが「71（17×4に、Mの下2けたを4倍してくり上がってくる3を加えたもの）」になることはあり得ます。
また、それ以降、Mの上2けたが「18」から「24」まで調べても、条件を満たすようなものはありません。
よって、Mの十の位以下を切り捨てた値として考えられる整数は1700のみとなります。
　時間内に見つけられたかどうか、差のついた1問でした。

(3)

「Mを4倍するとNになる」
「Mの千の位とNの百の位は等しく、また、Mの百の位とNの千の位は等しい」
「Mの十の位とNの一の位は等しく、また、Mの一の位とNの十の位は等しい」
という2つの条件を満たすMの下2けた（十の位と一の位）を考えます。
(2)であったように、Mの下2けたを4倍したとき、上に3くり上がらなければならないので、Mの下2けたは
300÷4＝75
以上なければなりません。
　Mの下2けたが「75」のとき、Mを4倍したNの下2けたが「57」になることはありえません。
4倍すると必ず偶数になるため、そこに気付ければ、Mの下2けたは75～79と90～99は調べる必要がありません。
　Mの下2けたが「80」のとき、Mを4倍したNの下2けたが「08」になることはありません。
　Mの下2けたが「81」のとき、Mを4倍したNの下2けたが「18」になることはありません。
　Mの下2けたが「82」のとき、Mを4倍したNの下2けたが「28」になります。
　それ以降も調べても条件を満たすものはありません。
　よって、Mとして考えられる整数は「1782」のみとなります。
　(2)同様、差のつく1問でした。

　例年出題される速さの問題です。
　長い文章から状況を正確に読み取り、進行図を丁寧にかく必要があります。
　3人が登場する旅人算で、速さも異なるうえに向きも異なります。さらには休憩もあることから、このようなタイプの問題においては「ダイヤグラム」が有効でしょう。
　作図処理に慣れている受験生にとってはさほど難易度は高くありませんが、この処理で戸惑った受験生と比較すると差がつきやすい問題だったと言えます。

(1)

　ア＝180度－角ACB
　イ＝180度－角CAB
なので、
　ア＋イ＝180度－角ACB＋180度－角CAB
　　　　＝180度＋180度－(角ACB＋角CAB)
　　　　＝360度－90度
　　　　＝270度
と求まります。
　確実に正解したい1問です。

(2)

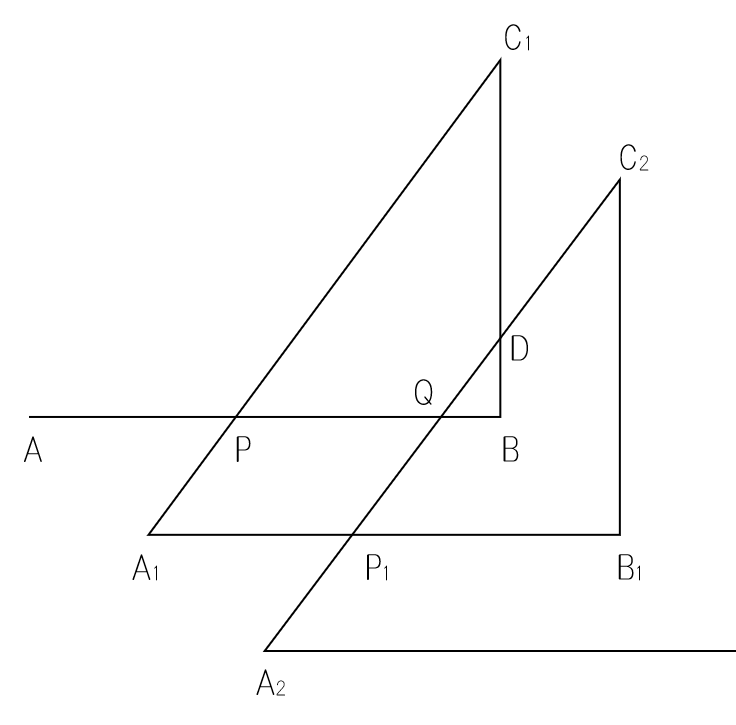
上図の三角形PBC1はPB：BC1：C1P＝3：4：5の直角三角形です。
　BC1は3cmなので、PBの長さは
　3÷4×3＝2.25（cm）
となり、QBの長さは
　2.25×2－4＝0.5（cm）
と求まります。よって、BDの長さは
　0.5÷3×4＝ （cm）
となります。
　合格のためには正解したい1問でした。

(3)

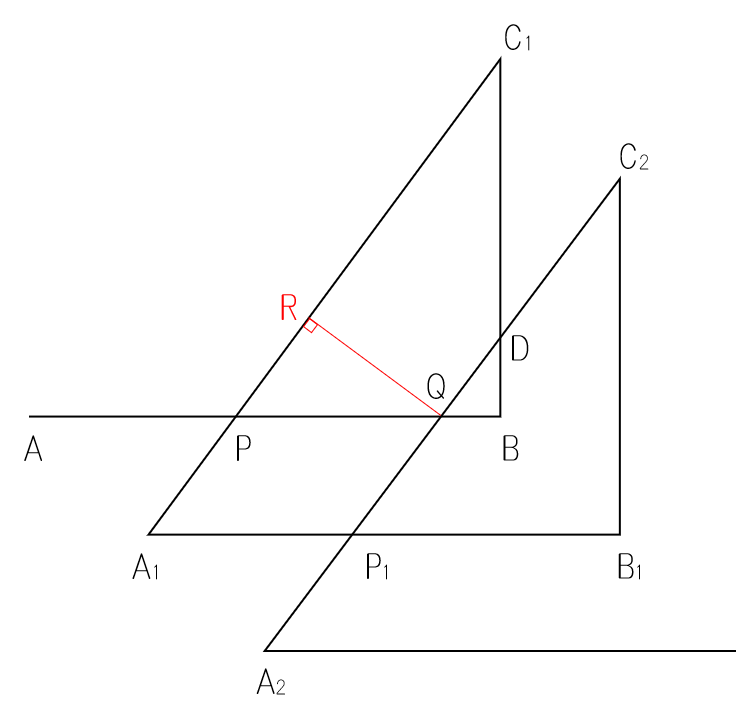
　求めるのは上図のQRの長さです。
　PQの長さは
　2.25－0.5＝1.75（cm）
なので、QRの長さは
　1.75÷5×4＝1.4（cm）
と求まります。
　合格のためには正解したい1問です。

(4)

　4＋3＋5＝12（cm）
を1つの周期として考えたとき、全部で2021cm移動するということは
　2021÷12＝168あまり5
より、168周期と残り5cm進むことがわかります。
　「周期数」と、そのときに「平面が何個の部分に分かれたか」を調べます。
　周期数が1のとき、平面は2個の部分に分かれます。
　周期数が2のとき、平面は5個の部分に分かれます。
　周期数が3のとき、平面は8個の部分に分かれます。
　周期数が4のとき、平面は11個の部分に分かれます。
このように、周期数が1増えるごとに、平面の数は3個ずつ増えていきます。
　よって、周期数が168のとき、平面は
　2＋3×(168－1)＝503（個）
となります。（※残り5cm進んでも、それによって平面の数は増えません。）

合否を分けた一題

(1)

立体Ｘは上図の立体ASUQE-MTGRであり、面の数は7とわかります。

(2)

立体Ｘの体積は四角柱ANCM-EQGRから三角すい台NUS-CGTを引いて求めます。
三角すいB-CGTと三角すいB-NUSは相似比が2：1の相似な立体なので、体積比は8：1であり、三角すい台NUS-CGTの体積は三角すいB-CGTの体積のとわかります。
　BR：RD＝2：1なので、三角すいB-CGTの体積は三角すいB-CDGの体積のです。
　よって、三角すい台NUS-CGTの体積は
　
と求まります。また、四角柱ANCM-EQGRは
　3×6×6＝108（㎤）
なので、求める立体Ｘの体積は
　108－21＝87（㎤）
となります。

(3)

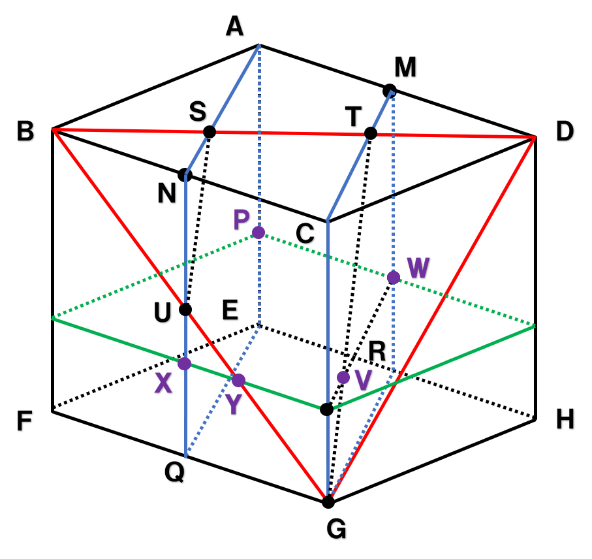
立体Ｘと、切断面との交点をチェックすると、上図の点Ｐ，Ｖ，Ｗ，Ｘ，Ｙの5つなので、これらを結んだ五角形ＰＶＷＸＹが求める図形となります。
この図形を真上から見ると、次のようになります。

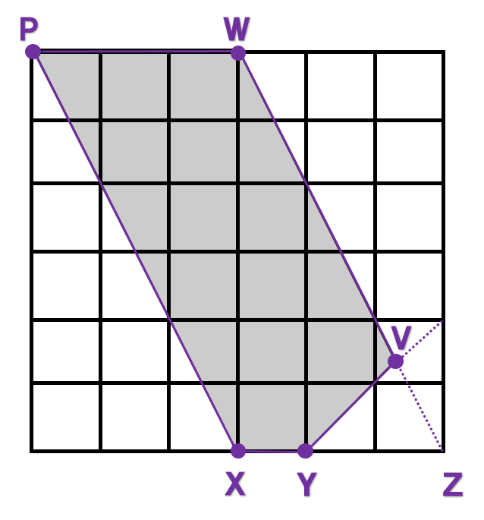
　三角形VYZの面積は
　
なので、求める五角形の面積は
　
となります。

この記事は役にたちましたか？

(まだ評価されていません)

 Loading ...