算数の合否を分けた一題
聖光学院中入試対策・算数の合否を分けた一題(2018年度)
難易度分類
| 1 | (1) A (2) B (3) B |
|---|---|
| 2 | (1) A (2) A (3) C |
| 3 | (1) B (2) B (3) B |
| 4 | (1) A (2) A (3) A (4) A |
| 5 | (1) B (2) B (3) C |
A…聖光学院中合格を目指すなら、確実に得点したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難度、処理量から判断して、得点差がつかない問題
平成30年度 出題総評
合格者平均/満点 = 117.0点/100点
受験者平均/満点 = 94.1点/150点
でした。
見た目がとっつきにくく、難しそうな問題が多く、過去問より難しく感じた受験生も多かったように思いますが、結果的には聖光学院の算数としては平均的なレベルとなりました。
一見して難しそうでも、やってみれば難しくない問題と、やはり難しい問題の見極めが重要です。
今年度は大問3の速さ、大問5の図形で差がついたと思われます。大問5の図形を、合否を分けた一題として取り上げます。
問題別寸評
(1)
クセのない計算。差はつかないでしょう。
(2)
全部足せば家族の和の3倍になることに、どこで気がつくか。
3量を処理は多く経験していると思います。ここでは5量です。まずは書き出して、全体像が見えたときにはじめて全体を足すことに気が付くのではないでしょうか。書き出す手際で差が付きそうです。
〇、△、□などで表そうとすると、5量は厳しそうです。母=①として、できるだけ〇を使って表す方針をとれば、強引に求めることもできます。
(3)
見慣れない形に一瞬戸惑いますが、倍数条件を考えて候補を書き出し、条件で絞り込んでいけば答えにたどり着くので、実際にはさほど得点差はついていないと思われます。条件の見落としに注意して、焦らず丁寧に探しましょう。
1からある整数までの総和、すなわち三角数に関する問題です。
(1)
導入用の問題。ミス注意。
(2)
2016年入試では、2016の素因数分解形とともに、2016が第63番目の三角数であることまで対策として頭に入れていた受験生が多くいたと思われます。このことを知っていれば、B=2が瞬時に出てくるわけですが、さすがに今年の受験生にそれを求めるのは酷でしょう。2018以下の三角数で最大のものを求める、ということさえわかればあたりをつけてあっさり求めることができます。
(3)
まず表に書き出して整理し、規則を読み取ることを考えましょう。
| 整数 | A | B |
|---|---|---|
| 1 | 1 | 0 |
| 2 | 1 | 1 |
| 3 | 2 | 0 |
| 4 | 2 | 1 |
| 5 | 2 | 2 |
| 6 | 3 | 0 |
| 7 | 3 | 1 |
| 8 | 3 | 2 |
| 9 | 3 | 3 |
ここから規則性を考えて、求める和が
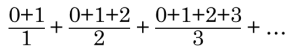
の形で求められることに気づけば、何とかなりそうですね。
もし、先が見えない、時間がかかりそう、と感じたら躊躇なく後回しするのが賢明でしょう。
問題文が長いです!聖さん、光さん、学さんが登場します。頑張って読んで、情報を整理することを考えましょう。
もし…なら、という形で、3通りの速さで進んだ場合の到着時刻を比べていくことになります。複数のパターンを同時に比較するので、ここではダイヤグラムを書くのが得策でしょう。頑張って情報を整理できれば、設問そのものは難しくないので、やったもの勝ち、と言える問題でした。この問題を回避すると、得点率8割は難しいでしょう。
(1)
同じ速さで到着時刻が22分差ということなので、出発時刻の差も22分です。学さんが出発する6分前までに光さんは22-6=16分歩いていました。16分歩いた道のりを引き返して6分経過しているので、P地点まであと10分かかるところですが、学さんも同じ速さで歩き出したので、5分で出会います。以上より
16+6+5=27分
と求められます。
(2)
速さ比 3:5より
時間比 5:3 →差の2が、21.6分ですから、時間の5は、54分にあたります。
以上より、54-(16+6)=32 分後です。
(3)
時間比 54:42より
速さ比 7:9 →差の2が、20m/分ですから、速さの7は、70m/分にあたります。
求める距離は、70×54=3780m
図形の重なりを調べて、塗られている部分を推理する問題です。設定が思いのほか易しいため、正解率は高かったものと考えられます。
(1)
対称性の問題です。四つ折りにしたハンカチを対角線でさらに半分にした状態を考えます。この直角二等辺三角形の塗り方さえ決めればよい、ということにすぐ気がつくでしょうか。
これに気づけば、3マスの塗り方を決めればよいので、各マスを塗るか塗らないかを考えて、
2×2×2=8通り
と求められます。
(2)
グラフから、重なっている部分が含む黒い正方形の枚数を容易に読み取ることができます。
| 時間 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 面積 | 0 | 0 | 32 | 16 | 48 | 32 | 0 |
| 黒い正方形の枚数 | 0 | 0 | 2 | 1 | 3 | 2 | 0 |
図形Aを縦4列に分けて考えます。
右から順に、2個,1個, 3個, 2個であることがわかります。各列の塗り方を考えて、
6通り×4通り×4通り×6通り=576通りと、すんなり求めることができるでしょう。
(3)
考える余地のない問題で、一瞬戸惑うかも知れません。慎重に答えましょう。
(4)
(2)と全く同じ手順で捌きます。難しくしたつもりかもしれませんが、難しくなってはいません。
図4を上から4㎝刻みに4等分します。各段の黒い部分の高さは上から順に
4㎝、2㎝、1㎝、0.5㎝となっています。
グラフから、重なり部分の高さの合計を読み取ります。
| 時間 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 面積 | 0 | 0 | 6 | 2 | 28 | 6 | 0 |
| 高さの合計 | 0 | 0 | 1.5 | 0.5 | 7 | 1.5 | 0 |
| 1段目 高さ4㎝ | ● | ||||||
| 2段目 高さ2㎝ | ● | ||||||
| 3段目 高さ1㎝ | ● | ● | ● | ||||
| 4段目 高さ0.5㎝ | ● | ● | ● |
高さの合計を見れば、どこを塗るかは自動的に決まるので、塗るところを●印で表しました。
2秒後から5秒後の●印の部分を、図形Aの右から塗りつぶすだけです。
合否を分けた1題
大問5を取り上げます。大問3をしっかり得点して、なおかつ大問5で得点できていれば、合格は間違いないと思われます。
空間図形を扱う際は、ある方向から見て、平面図形としてとらえ直すのが定石です。この問題では、上から見た図を描きます。
(1)
上から見た図を描くと、AB方向とAD方向の長さがわかります。上から見た図の中で、QとRに来るためのXとYの秒数を求めます。RはこのあとAE方向に下がっていくので、QR;RC=3:1からAE方向に2.5㎝進むとわかり、オ=2.5÷1=2.5秒と求めることができます。
(2)
まずZ=0秒として、平面で考えさせます。
「点Pが通過する可能性のある部分」が考えにくいです。4秒後に点Pが到達する場所、すなわちゴールを考えれば、ゴールとスタートの間が通過部分だと考えることができます。
Xを押す時間を変化させて、Yを押す時間を考えましょう。
| X | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Y | 4 | 3 | 2 | 1 | 0 |
この5通りのボタンの押し方でPが到達する点を図示すると、数の赤い点になります。

ここまで書けば、到達点は下のような直線で表せることがわかります。あとは塗りつぶすだけです。
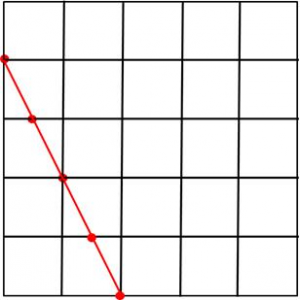
(3)いよいよ3次元に入ります。X,Y,Zの3つの時間が出てきますが、(2)と同じように
Z=0, Z=1, Z=2, Z=3…とZを固定して、それぞれについて平面上の到達点を考えます。
Z=0のとき X+Y=8
| X | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| Y | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
これより、Z=0,すなわち正方形ABCD上におけるPの到達点は、下の図のようになります。
正方形からはみ出した点は、正方形ABCDの平面を延長した場合の到達点ということになります。
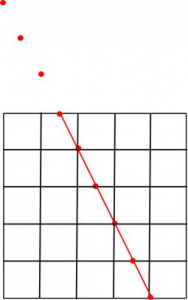
以下、同様にZ=1, Z=2, Z=3…と調べていきます。高い所から順に、水平な切り口を考えていきます。CTスキャンのイメージです。各切断面における到達ラインは下の図のようになります。
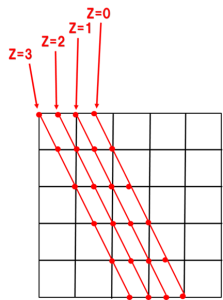
Z=8のときまで調べましょう。この作業によって、到達点の集合が立方体内部の平面であることがわかります。
この平面によって切り取られる立体の形は…三角錐台です。Pの通過領域はこの三角錐台になります。ここまでくればゴールは目前です。
大問5を攻略するためには、
①通過範囲を、到達点から考える
②Zの時間を固定して、各切断面を調べる
の二つが必要です。
上から順に切断面を調べる作業は多く経験しているものですが、①や②の発想を使う機会は多くありません。それだけ対応が難しい問題でした。
出題意図としては、
地道な作業で調査→全体像の把握
ができるかどうかを見ていると思います。どんな作業をしたら調べることができるかを、自分で考える習慣が大切と言えるでしょう。
聖光学院中入試対策・関連記事一覧
聖光学院中入試対策・同じ教科(算数)の記事
聖光学院中入試対策・同じテーマ(合否を分けた一題)の記事
- 社会の合否を分けた一題(2010年度)
- 算数の合否を分けた一題(2015年度)
- 国語の合否を分けた一題(2015年度)
- 社会の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2016年度)
- 国語の合否を分けた一題(2016年度)
- 理科の合否を分けた一題(2016年度)
- 国語の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2017年度)
- 社会の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2018年度)
- 国語の合否を分けた一題(2018年度)
- 理科の合否を分けた一題(2017年度)
- 社会の合否を分けた一題(2018年度)
- 理科の合否を分けた一題(2019年度)
- 国語の合否を分けた一題(2019年度)
- 社会の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2020年度)
- 社会の合否を分けた一題(2020年度)
- 理科の合否を分けた一題(2020年度)
- 社会の合否を分けた一題(2021年度)
- 算数の合否を分けた一題(2021年度)
- 理科の合否を分けた一題(2021年度)

 (2 投票, 平均値/最大値: 4.50 / 5)
(2 投票, 平均値/最大値: 4.50 / 5)