算数の合否を分けた一題（2016年度）

算数の合否を分けた一題

聖光学院中入試対策・算数の合否を分けた一題（2016年度）

難易度分類

［１］	(１)Ａ　　(２)Ａ　　(３)Ｂ
［２］	(１)Ａ　　(２)Ａ　　(３)Ｃ
［３］	(１)Ａ　　(２)Ｂ　　(３)Ｂ
［４］	(１)Ｂ　　(２)Ｂ　　(３)Ｂ
［５］	(１)(ア)Ａ　　(イ)Ａ　　(２)Ｃ

A…聖光学院中学合格を目指すなら、確実に正解したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難易度、処理量から判断して、得点出来なくとも差がつきにくい問題

問題別寸評

［１］

(１)

□にあてはまる数を求める問題です。手順通りやれば問題ありません。0.625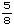＝は覚えておきましょう。

(２)

100から999までの整数の中で、21と互いに素な整数がいくつあるかが問われています。21＝３×７より、21と互いに素な整数は３の倍数でも７の倍数でもないものです。ベン図を描いて正確に処理しましょう。

(３)

問題の見取り図と選択肢の展開図の各面を対応させて、ふさわしくないものを選びましょう。正解の選択肢自体は比較的選びやすいものでした。

［２］

(１)

N進法の問題です。６までの数が使えるという条件から７進法とわかります。ここで６進法としないことが１つ目の注意点です。１番目が０であるため、答えが１つズレてしまうことにも気を付けましょう。

(２)

(１)と同様に答えが１つズレることに注意しましょう。また、(１)と作業を逆にしてはいけません。

(３)

６が使われていないものを桁数ごとに整理しても良いですし、余事象を利用して６が使われていないものを(１)の答えから引くのも良いです。正確に数え切った受験生は少なかったと考えられます。

［３］

(１)

詳しくは後で述べますが、(３)まで場合分けと計算で処理できる場合の数です。問題文に例が書いてあるときは決して読み飛ばさず、例と同じ作業をして同じ過程・結果になることを確認してから問題に臨んでください。

(２)

正六角形の頂点にコマが来るのは大きく分けて２つのパターンがあります。１つ目を見つけた時点で答えが出たと思い込んで結論を下さず、他の場合もあるかもしれないと疑いながらコマの動き方を試してみましょう。また、(２)のみ解き方を記述する形式になっています。採点者に伝わるような答案が書けていたかどうかも重要なポイントでした。

(３)

サイコロを４回振る分、場合分けは増えますがポイントは(１)と同様です。場合の数の考え方が身についている受験生にとっては(３)まで比較的解きやすかったのではないかと考えられます。

［４］

(１)

光さんチームは複数人で往復を繰り返すので、全体の動きを捉える方法としてはダイヤグラムが望ましいです。線路沿いを歩く人が電車とすれ違い、追い抜かれる問題と要旨は同じです。(１)は速さの差が問われているので、追い抜かれる時間と距離の差に注目しましょう。

(２)

(１)で速さの差を求めたので、同様に速さの和を求めることを考えてください。すれ違う時間と距離の和から速さの和が求められたら、あとは和差算です。(３)のために光さんチームの速さも求めておくとよいです。

(３)

発想は(１)・(２)と同様です。(２)で求めた聖さんの速さを1.2倍して、光さんチームとの速さの差を考えます。(１)に手がついたら、(３)まで取り切りたい問題です。

［５］

(１)

(ア)　７：24：25を使うことは明らかです。答えの数値は複雑にはなりますが、計算の手順自体は非常に少ないので、見直しをしつつ確実に正解したい問題です。

(イ)　(ア)と同様、手順は少ないが数値は複雑です。丁寧に計算しましょう。

(２)

回転した後の三角形を正確な位置関係で描くことができるかが最初のポイントです。三角形を描くことができれば相似・面積の比を利用します。ただし、(１)に比べて極端に難度が高いため、合否には直接影響しなかったものと考えられます。

合否を分けた一題

今年の入試から合否を分けた１題として取り上げるのは[３]です。[３]・[４]ともに(１)に対する着想次第で、大問１つ分の出来不出来が決まってしまう問題でした。[３]・[４]以外の問題は小問毎に易しいものと難しいものが比較的はっきり分かれており、今年の入試では[３]・[４]の２題が受験生間で差がつく問題でした。また合格者平均点84.7点は比較的低得点であることから、 [４]については手がつかない受験生が多く、[３]の出来が合否を分けたものと考えます。

(１)

サイコロを３回振って点Оに戻るときを考えます。㋐、㋑、㋒それぞれの方向について逆向きにコマを移動させることはできないので、点Оに戻るためには㋐、㋑、㋒それぞれの方向に同じ長さだけ移動しなければいけません。このとき考えられる㋐、㋑、㋒の方向へ移動した長さは、(㋐、㋑、㋒)＝(１㎝、１㎝、１㎝)、(２㎝、２㎝、２㎝)の２通りです。よって、３回のサイコロの目の組み合わせは(１、２、３)、(４、５、６)の２通りとなります。最後に各々について目の出る順番を考えて、
　　３×２×１×２＝12通り

(２)

正六角形の頂点にコマがあるのは、サイコロを３回振った結果、点Оからいずれかの方向に１㎝だけ離れた点にコマが来るときです。例えば、１、２、６の順に目が出たときは㋐の方向に１㎝、㋑の方向に１㎝、㋒の方向に２㎝コマを移動させます。㋒の方向も１㎝であれば(１)のようにコマは点Оに戻ることになりますが、㋒の方向への移動が１㎝長い分、コマは点Оから㋒の方向に１㎝だけ離れた点Ｅに移ります。同様に、４、５、３の順に目が出たときは㋐、㋑の方向に比べて、㋒の方向への移動が１㎝短い分、コマは点Оから㋒と逆の方向に１㎝だけ離れた点Ｂに移ります。つまり、移動させた長さが１方向だけ１㎝長いまたは１㎝短いときに正六角形の頂点にコマがあります。このとき考えられる㋐、㋑、㋒の方向へ移動した長さの組み合わせは、(１㎝、１㎝、２㎝)、(１㎝、２㎝、２㎝)の２通りですが、各々について㋐、㋑、㋒の順列が３通りずつあります。

よって、㋐、㋑、㋒の方向へ移動した長さは、３×２＝６通り
さらにサイコロの目が出る順番を考えて、３×２×１×６＝36通り

(３)

(１)と同様に、コマが点Оに戻るのは㋐、㋑、㋒それぞれの方向に同じ長さだけ移動したときです。このとき考えられる㋐、㋑、㋒の方向へ移動した長さは、(㋐、㋑、㋒)＝(２㎝、２㎝、２㎝)の１通りです。この長さをサイコロを４回振って移動させることを考えます。方向３つに対して移動は４回あるので、いずれか１方向は２回に分けて１㎝ずつ、残り２方向は１回で２㎝移動させます。㋐の方向へ１㎝ずつ２回移動させるときのサイコロの目は１が２回、５が１回、６が１回となります。この順番を考えて、
　　４×３＝12通り
㋑の方向へ２回、㋒の方向へ２回移動させるときも同様に、
　　12×３＝36通り

著者：受験Dr. (受験ドクター)

この記事は役にたちましたか？