理科の合否を分けた一題（2020年度）

理科の合否を分けた一題

聖光学院中入試対策・理科の合否を分けた一題（2020年度）

難易度分類

１	（１） A　　（２） A　　（３） A　　（４） A　　（５） A　　（６） B　　（７） (a) A　　(b) B　　(c) B
２	（１） B　　（２） B　　（３） C　　（４） A　　（５）(a) Ａ　　(b) B
３	（１） A　　（２） A　　（３） A　　（４） A　　（５） A　　（６）Ａ（７） B
４	（１） A　　（２） A　　（３） A　　（４） A　　（５）(a) A　　(b) A　　(c) B

A…聖光学院合格を目指すなら、確実に得点したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難易度、処理量から判断して、部分点を拾えれば良しとする問題

出題総評

2020年度の聖光学院は、例年通り、幅広い知識を問う問題と、少々長めの文章を読み取って、論理的に考えたり、数的処理を的確に行ったりして設問に答える問題が中心です。
100点満点で、合格者平均84.4点（昨年度79.8点）、受験者平均75.5点（昨年度70.5点）と、昨年度より上がっている理由としては、得点しやすい問題の割合が多かったことが考えられます。

生物分野の問題は、植物のつくりとはたらきについての問題。
地学分野の問題は、月の運動と月食についての問題。
化学分野の問題は、物質の分類と砂糖の燃焼に関する問題。
物理分野の問題は、電流がつくる磁界とリニアモーターカーについての問題。

生物→地学→化学→物理　の流れは、ここ数年定着しています。
本年は、物理分野に計算問題がなかったかわりに、地学と化学でかなり手間のかかる計算問題が出されたため、そこで時間をかけすぎないようにする工夫が必要でした。
生物・地学・化学分野の知識問題は、比較的平易な問題が大部分で、その中にかなり詳しいことがらを問う問題がちりばめられています。ミスを恐れずテキパキと処理し、余裕をもって計算問題取り組むことができれば、高得点が狙えたのではないでしょうか。

対策としては、知的好奇心をもち、普段から積極的に調べ学習に取り組み、広く知識を吸収しておくこと。計算問題に多くあたり、いろいろなアプローチ方法を身につけておくこと。比較的長めのリード文の読み取りに慣れておくことなどがあげられます。

問題構成は、４分野から大問４題、小問38問。
解答形式は、記号選択が29問、数字が６問、言語が２問、記述が１問。作図とグラフはありませんでした。
昨年と比べ、記号選択が13問増加していますが、うち４問は、計算が必要なものでした。本年は、組み合わせの選択肢が多用され、その点では選びやすくなっています。
言語は、基本の知識でした。
記述は、10～20字程度。
計算が必要な問題は、記号選択の形式のものと合わせると10問なので、ボリュームとしては昨年と同程度です。

問題別寸評

１

（生物）植物のつくりとはたらきについての問題です。
植物のつくりに関する基本の知識問題から、顕微鏡による観察の仕方にからめた問題へ展開しています。観察についての問題では、実際にプレパラートをつくって、葉緑体を顕微鏡で見たことがある生徒には有利だったのではないでしょうか。

（１）

子葉のスケッチから、植物を特定する問題です。アサガオとマツは一目でわかります。
②は、子葉の先端がいびつに曲がっていますが、単子葉類であることは見て取れます。
組み合わせ選択肢となっているので、仮に②が特定できなくても、他の３つと手掛かりに選ぶことができたのではないでしょうか。

（２）

本葉のスケッチから、植物を特定する問題です。これも組み合わせ選択肢で、アサガオとタンポポがわかれば確定できるので、迷うことなく解答できたのではないでしょうか。

（３）　(a)

光合成によってつくられたデンプンは、水にとける糖に分解され、師管を移動して体の各部に運ばれます。これも基本の知識です。

（３）　(b)

ジャガイモやハスは茎、サツマイモやニンジンは根、イネやコムギは種子の胚乳、バナナは果実にデンプンを貯蔵します。
デンプンなどの栄養分を貯蔵している場所を、ヒトは栽培して食用にします。

（４）

似たような問題が続きます。
ピーマンの可食部は果実で、中の白い粒が種子です。ブロッコリーは茎とその先についたつぼみを食べています。

（５）

ジャガイモは地下茎、玉ねぎは葉に養分を蓄えていて、これを土に植えると、新しい芽を出します。
トマトとモモは、果実のなかにある種子が発芽します。

（６）

もやしは，光の当たらないところで育てます。もやしに光を当てると葉緑体が合成されて緑色になり、光合成ができるようになります。

（７）　(a)

４つのイラストから、オオカナダモを選ぶ問題です。
オオカナダモを見たことがなかったとしても、アはアオミドロ，イはワカメ，ウはウミガメとわかるので解答しやすいでしょう。

（７）　(b)

オオカナダモの葉は、スライスする必要なく、そのままプレパラートにすることができます。
観察を行ったことがあれば即答できますが、そうでなくても、顕微鏡についてのしっかりとした知識があれば、他の選択肢が間違っているとわかります。

（７）　(c)

かなり詳しい知識の問題になります。オオカナダモの葉の、細胞内の緑色の粒は葉緑体です。光合成は、葉緑体の中で行われるので、ヨウ素デンプン反応によって、葉緑体の粒が青紫色に染まります。葉緑体の外では、デンプンは水に溶けやすい糖に変えられているので反応しません。

２

（地学）月の動き方と月食についての問題です。
大問４題中、最も時間と手間がかかる問題となっています。
求めようとする値を計算するために、与えられた数値のどれを使えば良いかを、すばやく見極めなければなりません。さらに、比の考え方をきちんと使えるかどうかがポイントとなります。

（１）〜（３）

→合否を分けた１題で取り上げます。

（４）

基本の知識をチェックする問題です。
半影には、太陽の光の一部しかとどきませんが，本影は地球の影の中なので光がとどきません。

（５）　(a)

必要な数字はすべて図３に示されているので、リード文にそって計算すれば良い問題です。
ＣＦ：ＦＢ＝108：１
ＣＦ：（月の公転軌道の半径）＝390：１
したがって、（月の公転軌道の半径）：ＦＢ＝１：（390÷108）≒１：3.6

（５）　(b)

三角形の相似比は、光の進み方を図形的に考えるときなどによく使う方法です。

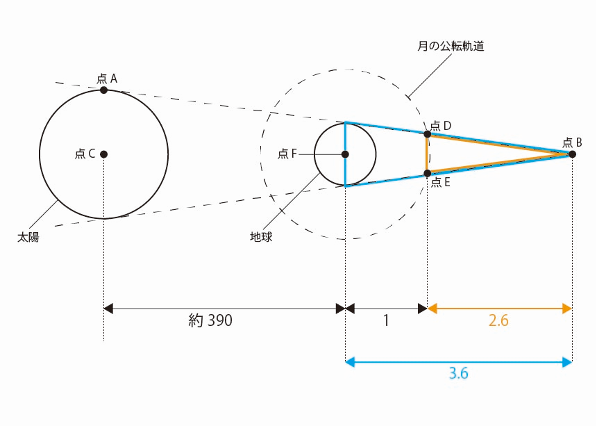
青い三角形：オレンジの三角形＝3.6：（3.6－１）＝3.6：2.6
したがって、ＤＥ＝地球の直径×（2.6/3.6）とわかります。

３

（化学）物質の分類と砂糖の燃焼に関する問題。
前半は、基本の知識の問題ですから、聖光学院受験生なら、確実に得点できるのではないでしょうか。燃焼の計算問題も、定石通り解き進めれば正解できる問題です。落ち着いて取り組むことが大切です。

（１）

磁石にくっつく金属は、鉄以外にニッケルとコバルトがあります。知識が確実に身についているかが問
われる問題です。

（２）

液体のエタノールは，水に無制限に溶けます。
エタノール以外の選択肢は、水にほとんど溶けないものばかりなので、選びやすかったのではないでしょうか。

（３）

フェノールフタレイン溶液の色の変化から，アルカリ性の水溶液を選びます。
炭酸水、レモン果汁、酢は酸性、エタノールは中性です。これも基本の知識です。

（４）

電解質の水溶液として、硝酸カリウム水溶液と塩酸を選びます。また、金属も電気を通すことから、はんだ（鉛とスズの合金）も選ぶことができます。ここでも幅広い知識が問われています。

（５）

実験１から、磁石にくっつくＢが、鉄とわかります。
実験２から、水に溶けないＣが、アルミニウムとわかります。
実験３から、水溶液がアルカリ性のＡが、重曹とわかります。
実験４から、非電解質のＥが、砂糖とわかります。
残ったＤは、食塩です。
これは、すんなりとわかったのではないでしょうか。

（６）

食塩における、ナトリウム原子と塩素原子の並び方を考える問題です。
①～③の図から、ナトリウム原子１個には水平方向に４個、上下に２個の、合計６個の塩素原子が接しています。塩素原子についても、同様に考えます。

（７）　(あ)

リード文の内容を、書き出して整理します。
砂糖342ｇ＝炭素144ｇ＋水素22ｇ＋酸素176ｇ
砂糖を燃焼させると、含まれている炭素が二酸化炭素、水素が水になります。
　炭素12ｇ＋酸素32ｇ→二酸化炭素44ｇ
　水素２ｇ＋酸素16ｇ→水18ｇ
よって，砂糖342ｇを完全燃焼させたとき、
　炭素144ｇに結びつく酸素は、32×144/12＝384（ｇ）
　水素22ｇに結びつく酸素は、16×22/2＝176（ｇ）
砂糖342ｇには、もともと酸素が176ｇ含まれているので、384＋176－176＝384（ｇ）の酸素が必要です。

（７）　(い)

砂糖342ｇに含まれている炭素144ｇが燃焼したとき発生する二酸化炭素は，144＋384＝528（g）です。

（７）　(う)

砂糖342ｇに含まれている水素22ｇが燃焼したとき発生する水は，22＋176＝198（g）です。

４

（物理）電流がつくる磁界とリニアモーターカーについての問題。
本年度は、物理分野の問題に計算問題がありませんでした。その一方で、長文と図を読みとる力が求められており、しっかり解き進めることができれば得点できるようになっています。

（１）

まずは基本です。電流のまわりには、右ネジの向きに磁界ができます。
磁界の中に方位磁針を置くと、磁界の向きにＮ極が向きます。

（２）

こちらも基本の知識です。
棒磁石のまわりの磁界は、Ｎ極から出て、Ｓ極に入る向きです。方位磁針の位置を取り違えないよう注意が必要です

（３）

これも基本の知識です。
右手の法則を使えば、すぐに答えがわかります。

（４）

Ｅ点の方位磁針の向きから、Ｆ点の方位磁針の向きがわかります。磁界の向きから、Ｆ点側がＮ極とわかるので、電流の向きも決まります。

（５）　(a)

リニアモーターカーの車体を進ませる力についての問題です。
車体には永久磁石、壁にはコイルがあることから、永久磁石と電磁石が、引きつけ合ったり、反発しあったりする力によって進むと考えます。
矢印の向きに動くには、永久磁石が、そのすぐ前の電磁石に引きつけられるように電流を流します。

（５）　(b)

(a)の方法で、永久磁石が電磁石に引きつけられても、そのままでは、車体がそこで止まってしまいます。
引きつけられたあとに、タイミングよく反発する力がはたらかせることで、進ませることが可能となります。そのために、壁のコイルに流す電流の向きを規則的に変えます。

（５）　(c)

最後に、リニアモーターカーの車体を浮上させる力について考える問題です。
図９では、永久磁石のＮ極が８の字コイルに向いています。車体を浮上させるには、上向きの力が必要なので、永久磁石は、上側のコイルに引きつけられ、下側のコイルと反発しあうと良いとわかります。
このようにして、リニアモーターカーは地面から浮いた状態で進むので、摩擦による減速や騒音をなくすことができるのです。

合否を分けた一題

例年、大問４の物理分野に計算問題が配置される聖光学院ですが、本年は物理分野に計算問題はなく、大問２の地学分野にボリュームをもって出題されています。
臨機応変に後回しにする判断ができたかどうか。後回しにしたとしても、読み取りや情報整理に時間が取られすぎずに的確に処理できたかどうかで合否を分けたと考え、この問題を取り上げました。
あとに続く（４）〜（７）ももちろんですが、リード文の数値と図を関連づけて必要な情報を取り出し、設問の意図にそった解答に結びつけていかなければなりません。

２　（１）〜（３）

（１）

月の公転軌道の円周の長さを、距離ではなく、月何個分にあたるかで答えます。
「月何個分」というのは、月の直径の何倍にあたるかということです。
リード文に出てくる数字のうち、「月の公転軌道の直径」「月の直径」を使って計算すると、770000×3.14÷3500≒690.8　となります。選択肢から選ぶ形になっているので、正面から計算するのではなく、770000÷3500＝220　を3.14倍すると考えて、690を選ぶと良いでしょう。

（２）

こちらも，解答形式は選択肢ですが，計算が必要な問題です。
「月の公転周期」が27日なので、月が１時間で公転する距離は、「（１）の答え」÷27÷24（時間）≒１より，アを選びます。

（３）

地球から見たときの月の動きは、地球の自転による東から西への動きに、月の公転による西から東へもどす動きが重なります。「地球の自転」は24時間で１周、「月の公転」は27×24（時間）で一周ですから、月は空を１時間に1/24－1/（27×24）＝26/（27×24）＝13/（27×12）（周）することになります。（１）の答えを使うと、690×13/（27×12）≒28　となります。

著者：S.O.

この記事は役にたちましたか？