理科の合否を分けた一題（2018年度）

理科の合否を分けた一題

聖光学院中入試対策・理科の合否を分けた一題（2018年度）

難易度分類

１	（１） a　B　　b　A　　c　A　　d　A　　（２） a　A　　b　A　　c　A　　d　C
２	（１） A　　（２） A　　（３） A　　（４） B　　（５） A　　（６） B　　（７） A　　（８） B
３	（１） B　　（２） A　　（３） A　　（４） A　　（５） A　　（６） A （７） A
４	（１） A　　（２） A　　（３） A　　（４） A　　（５） A　　（６） A （７） A　　（８） B

A…聖光学院合格を目指すなら、確実に得点したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難易度、処理量から判断して、部分点を拾えればよしとする問題

出題総評

2018年度の聖光学院は、例年通り、幅広い知識を問う問題と、少々長めの文章を読み取って、論理的に考える問題が中心です。誘導なく未習の題材を解かせる問題は鳴りを潜め、昨年度と比べて取り組みやすく、難易度はやや易化した印象です。
生物分野の問題は、ヒトの肺と呼吸について。
地学分野の問題は、ハワイ諸島の成り立ちについて。
化学分野の問題は、水溶液と金属・環境問題について。
物理分野の問題は、物体の密度と浮力・水の状態変化と熱量について。

聖光学院特有の、大問内で分野をまたぐ設問があり、知識を関連付けて考える力が問われています。
出題される題材は、特に偏りが見られず、毎年大きく入れ替わっています。
対策としては、知的好奇心を広くもち、普段から積極的に調べ学習に取り組むこと。理科という科目にしばられることなく、いわゆる大人の常識的な知識も知っておくこと。科学読み物などを利用して、文章を読み取る力をつけること。また、ことばの知識を使えるレベルにするとともに、論理的に説明する力をつけておきましょう。

問題構成は、４分野から大問４題、小問35問。
解答形式は、記号選択が11問、数字が10問、言語が9問、記述が3問、作図が1問、グラフが1問。
記号選択が４問減少し、言語・記述が２問ずつ増えています。
記述は、１行程度が１問と、10～20字程度のものが２問。
計算が必要な問題は5問で、特に煩雑な計算は必要としていません。
作図は、肋骨に肋間筋を書き入れるもので、導入問題があるものの、知識がないと難しかったかもしれません。
グラフは、氷→水の温度変化を書き入れるものでした。

問題別寸評

１

（生物）ヒトの肺と呼吸についての問題です。
気管の外側に軟骨があることや、肋間筋のつき方などは、高いレベルの知識問題です。
一方、肺胞や横隔膜について聞かれている問題は、基本の知識ですから、落とさないようにしましょう。

（１）　a

声帯が振動すると声が出ます。気管は気管支に枝分かれし、最終的には肺胞につながります。
気管の軟骨については、知らなかった生徒も多かったのではないでしょうか。気管の外側には、気管軟骨輪とよばれるC字型の軟骨が積み重なるようにあり、首を曲げても気管がつぶれてふさがらないようになっています。

（１）　b

指示に従って計算するだけの問題です。桁を間違えないように注意しましょう。
肺胞の半径は0.15㎜なので、肺胞１個の表面積は4×0.15×0.15×3.14（㎟）
肺全体では、4×0.15×0.15×3.14×300000000÷1000000＝84.78（㎡）

（１）　c

肺胞のまわりには毛細血管がとりまいていて、血液中の気体の交換を行っています。

（１）　d

心臓から出て肺に送り込まれる血液が通る血管ですから、肺動脈です。

（２）　a

横隔膜は膜状の筋肉です。

（２）　b

横隔膜に力が入り収縮すると、下にさがって肺が広がります。逆に、横隔膜がゆるむと上に上がります。

（２）　c

しゃっくりは、横隔膜の痙攣によっておこります。

（２）　d

肋間筋は、肋骨と肋骨をつなぐ筋肉です。肋間筋が縮んだときに、肋骨が持ち上がって肺が広がるようになっています。かいてみれば、そうむずかしいしくみではないのですが、知らない生徒にとっては、かききることは難しかったかもしれません。

２

（地学）ハワイ諸島の成り立ちについての問題です。
文章をしっかり読み、見つけた手がかりをもとに考える問題です。多角的な視点から構成される問題に対応するためには、広い知識と因果関係を考える思考力が必要です。

（１）

地理の知識です。ハワイに旅行したことがある生徒には、易しかったのではないでしょうか。

（２）

これも地理の知識です。ハワイ諸島は、太平洋の中ほどに位置します。

（３）

西ノ島は、小笠原諸島の無人島で、海底火山の活動によってできた島です。1973年と2013年に噴火があり、新しくできた陸地は元あった島と一体化しました。
日本にあって火山や地震に関する話題は重要です。特に、５年以内に活動していたものについては、整理しておぼえておきましょう。

（４）

なだらかな形の火山をつくるマグマは、粘り気が少なく、さらさらと海に流れていきます。マグマの粘り気は、温度が下がるにしたがって増し、最後には固まってしまいます。

（５）

天文台に適したところは、空気が澄んでいるところです。標高4205ｍのマウナ・ケア山は、山頂付近が下層雲より高く、雲がかかることが比較的少ないといえます。また、赤道に近いほど、北半球の星座と南半球の星座を広く観察することができます。

（６）

（６）と（７）では、地形と気象の関係について考えます。
日本の北陸地方では、海からのしめった空気が山にそってのぼり、上昇気流となって雲ができます。カウアイ島の周囲にはあたたかくしめった空気があり、ワイアレアレ山にぶつかって上昇気流となって雲ができ、多くの雨がふります。よく似た気候としては、日本の屋久島があげられます。屋久島はほぼ全域が山地で、1000mから1900mの山が海から突き出ているような地形をしていて、ほぼ毎日雨が降り、山頂近くは毎年10000mm前後の降水量があります。

（７）

文中に「最も新しくできたハワイ島」「カウアイ島はおよそ500万年前にできたと推測されています。」とあります。カウアイ島ができてから500万年の間に、動植物の種類は増えていると考えられます。
また、「ハワイ島の中で最も高い山は標高4205ｍのマウナ・ケア山」「（カウアイ島の）最も高い山は標高1598ｍ」とあります。富士山より高いマウナ・ケア山では、雪が降ることがあります。他にも、赤道直下の地域であっても、5000ｍ級の山では氷河が存在することがあります。おぼえておきましょう。

（８）

ハワイ諸島は、ハワイ・ホットスポットでできた火山島が、北北西に移動してできました。島ができたのは、古い順に、カウアイ島・オアフ島・マウイ島・ハワイ島です。
カウアイ島ができてからハワイ島ができるまでの499万年間（500万－1万）の間に、カウアイ島は400㎞移動したと考えられるので、プレートが移動する距離は１年間に、
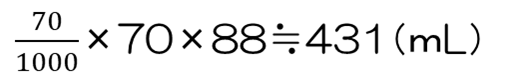
2018_gouhi_rika_1

３

（化学）水溶液と金属・環境問題についての問題。
これも、文章をしっかり読み、見つけた手がかりをもとに考える問題です。
酸性雨の原因とその影響の話題から、燃料電池などの環境に配慮した技術についてへと展開されています。

（１）

知識問題です。ブロンズは銅とすずの合金で、青銅ともよばれます。十円玉もブロンズです。年月がたつと酸化されて緑青になります。おぼえておきましょう。

（２）

空気中の窒素や酸素は水にほとんど溶けませんが、二酸化炭素は水にとけて酸性を示します。

（３）

酸性雨の原因物質は、二酸化硫黄（SO2）と窒素酸化物（NOx）です。火山ガスの主成分は水蒸気・二酸化炭素ですが、二酸化硫黄（亜硫酸ガス）もふくまれています。

（４）

NOxは窒素酸化物のことで、窒素と酸素が結びついてできる物質です。
「一緒に取り込んだ空気で燃焼させる」とあるので、空気に多くふくまれている窒素が関係していると考えるとよいでしょう。

（５）

これは常識です。燃料電池は、水素と酸素が結びつくことで水ができるので、環境に負荷が少ないと考えられます。

（６）

水素の性質は、基本中の基本です。最も軽い気体である水素は、実際に気球に使われてきましたが、引火爆発の危険性から、ヘリウムガスなどに変わってきています。

（７）

表１から、塩酸100ｍL・200ｍLではアルミニウムがあまり、300ｍLで過不足なく反応し、400ｍL・500ｍLでは塩酸があまっていることがわかります。塩酸100ｍLあたり、水素が1.12L発生することから、200ｍLでは２倍の2.24L発生します。→ア
表２から、塩酸100ｍL・200ｍLでは亜鉛があまり、300ｍL・400ｍL・500ｍLでは塩酸があまっていることがわかります。イには2.8が入ります。
表１と表２で共通している塩酸の量と基準にして判断します。特に計算する必要はありません。

４

（物理）物体の密度と浮力・水の状態変化と熱量についての問題。
（１）～（５）・（７）は、密度と浮力の問題。（６）・（８）は熱量と状態変化の問題です。
どちらも、定石通りに解けばよい問題です。

（１）

この金属の密度は6（ｇ/㎤）、体積は125（㎤）（5×5×5）です。
６×125＝750（ｇ）

（２）

ばねばかりの値は、浮力の分だけ小さくなります。水による浮力は、（水中の部分の体積×1.0）（ｇ）なので、750－125＝625（ｇ）

（３）

食塩水による浮力は、125×1.2＝150（ｇ）
ばねばかりの示す値は、750－150＝600（ｇ）

（４）

食塩水の液面から、氷が一部を出して浮いています。このとき、氷の重さと浮力はつり合っています。

（５）

（４）から、「氷全体の重さ＝液面より下にある部分の氷と同じ体積の食塩水の重さ」の関係がなりたちます。
氷の重さ＝0.9×125＝112.5　
液面より下にある部分の氷と同じ体積の食塩水の重さ＝（水面より下にある部分の体積）×1.2
ですから、
（液面より下にある部分の体積）＝112.5÷1.2＝93.75（㎤）
液面より出ている部分の高さは、
（125―93.75）÷25＝1.25（㎝）

（６）

このヒーターは、0.8Lの水を40秒で10℃（20－10）上げることができます。
1Lの水を1℃上げるには、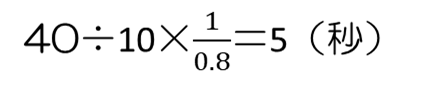 2018_gouhi_rika_2 必要です。

（７）

氷の密度と体積から、0.9×125＝112.5（ｇ）

（８）

→合否を分けた一題参照。

合否を分けた一題

本年も、いろいろな視点から多角的にアプローチされている問題がちりばめられているなかで、【４】の問題は、普段の演習で身に着けた技術をそのまま活かすことができる問題でした。
その中で、最後のグラフの問題は、（７）までの答えを手がかりに、容器の中がどのようになっているのかを考えながらかきます。ここまでしっかり正答できたうえで、どの要素を利用するかを的確に判断して対応します。

４

（８）

グラフの横軸は「加熱器の電源を入れてからの時間（秒）」、たて軸は「氷または水の温度（℃）」です。
加熱をはじめたとき、容器には０℃の氷が入っていました。
実験５は、「０℃の氷→０℃の水→96℃の水」の変化を観察するものです。
グラフは、「０℃の氷→０℃の水」の間は０℃で一定です。また、「０℃の水（氷がすべてとけたとき）→96℃の水」の間は、同じ割合で水温があがります。「電源を入れてから99秒後に、水の温度が96℃になりました」とあるので、氷がすべてとけた時間を逆算します。
（７）の氷がとけてできた水は、112.5ｍLです。
このヒーターを使って、0℃の水112.５ｍLを96℃にするには、
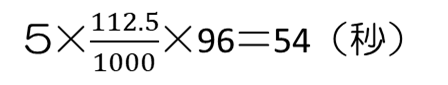2018_gouhi_rika_3 必要です。
つまり、99秒後より54秒前に、氷がすべてとけ、水温が上がり始めたと考えます。
グラフは、0～45秒までは0℃で一定の直線と、45秒後の0℃から、99秒後の96℃までを結んだ直線でかくことができます