算数の合否を分けた一題
桜蔭中入試対策・算数の合否を分けた一題(2021年度)
難易度分類
| Ⅰ | (1)A (2)B (3)㋐A ㋑A ㋒A (4)A (5)B …解答箇所5つトータルで (6)B |
|---|---|
| Ⅱ | A |
| Ⅲ | A・B |
| Ⅳ | (1)A (2)①A ②A |
A:桜蔭合格を目指すなら必ず得点すべき問題
B:着眼点や解法ツールにより正答率・かかる時間に差がつく問題 ➡ 合否を分けた一題
C:難易度や処理量から判断して、得点できなくても合否に影響しない問題
問題別寸評
(1)計算問題。
今年度の中学受験入試で出題された計算問題で、おそらくベスト3に入るであろう煩雑さ。桜蔭を目指して準備してきた受験生であっても、この計算問題ひとつに5分以上時間をとられた受験生が多かったようです。
与えられている分数の分母が91,13,7であることから、分母は極力計算せずに、7×13×△のようにかけ算の式のまま残しておくことで計算量を減らすことができます。とはいえ、それでも相応の計算量が求められる、桜蔭らしい出題でした。
上記の難易度分類では、計算問題は落としてほしくないという理由でAとしていますが、限りなくBに近いととらえてください。
(2)周期
①周期は5色と明白なので、1/1~10/1までの日数を正しく計算できれば問題ないでしょう。
②3/31の色を求めれば、4月の黒の日付が確定します。日付の合計は、6日間しかないのでそのままたす、等差数列の和として計算する、どちらでも構いません。
(3)数の性質
①桜蔭志望者であれば、素因数分解による約数の個数の求め方だけでなく、約数の総和の求め方もおさえているはず。「2けたで最大」という条件より、99から順に調べ上げる方針が確実です。
②約数が3個の整数、つまり「素数の平方数」がテーマです。求める素数の平方数を「㋐×㋐」と文字で表し、1以外の約数(2個だけです)の総和を表すと ㋐×㋐+㋐=㋐×(㋐+1) となり、これが1406です。差が1の2数の積なので、一の位のペアは2と3か7と8の2組に絞られます。30×30=900、40×40=1600より、40に近いので37と38で確定です。よって、37×37=1369。
これから桜蔭を目指す受験生は、このように文字や記号を用いて式を作ることに慣れておきましょう。
③設問①でも登場した、素因数分解による約数の個数の求め方がわかっていれば、瞬時に答えが求められます。
④約数4個の整数です。「素数の立方数」のパターンは,2×2×2と3×3×3の2個だけ。
「素数×別の素数」のパターンはもれなく書き出しましょう。2×□(□は2より大きい数),3×□(□は3より大きい数),5×□(□は5より大きい数)と順に調べ上げると、17個あります。よって、合わせて19個です。
(1)
2018年度大問Ⅱ(2)の正六角形に24枚の白黒の正三角形を敷き詰める問題と同趣旨の出
題です。2018年度は上記問題をとばして、他の問題に時間を割いた受験生が順当に合格しました。今回もアのみ拾って、あとはとばすというのが賢い選択でしょう。
どうしても解きたい!という、来年以降の桜蔭志望者のために、以下解答手順を記します。
問題文中に場合分けが例示されているので、それにしたがって解き進めていくのが無難です。
対称性を考えながら、重複を避けて調べ上げることができるかがカギです。
1枚のとき
四すみの1枚をとりかえるのが1通り
四すみ以外の1枚をとりかえるのが1通り
合計2通り。
3枚のとき
四すみの3枚をとりかえるのが1通り
四すみ以外の3枚をとりかえるのが1通り
四すみの2枚と四すみ以外の1枚をとりかえるのが6通り
四すみの1枚と四すみ以外の2枚をとりかえるのが6通り
合計14通り。
4枚のとき
四すみの4枚をとりかえるのが1通り
四すみ以外の4枚をとりかえるのが1通り
四すみの3枚と四すみ以外の1枚をとりかえるのが4通り
四すみの1枚と四すみ以外の3枚をとりかえるのが4通り
四すみの2枚と四すみ以外の2枚をとりかえるのが10通り
合計20通り。
(2)
5枚は3枚のときの白黒逆転、6枚は2枚のときの白黒逆転、7枚は1枚のときの白黒逆転、
8枚は0枚のときの白黒逆転となるので、設問(1)が完答できれば、自動的に設問(2)の答えは出てきます。1+2+8+14+20+14+8+2+1=70通りです。
ここから問題用紙2枚目です。
(1)
グラフの読み取りは平易です。唯一与えられている時間の29.5分後に着目し、そのときの水
量を求めて29.5分でわっておしまい。底面積を比で処理すれば、多少は計算の分量を減らすことができます。
(2)
前問で底面積を比にせず、水量計算を行っているのであれば、5段目までの水量が4100㎤、7段目までの水量が5900㎤と求めています。その比例関係を利用して、
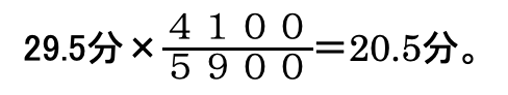
(3)
もっとも短い時間で水を止めるには、段数をできるだけ少なくすればよいので、2段にすればよいことがわかります。よって、和が12になる2個の整数の組合せを調べる和分解に帰着します。
(4)
19.7分で入れた水量と立方体12個分の体積の合計を容器の底面積でわれば、何段まで立方体を積んだかがわかります。計算すると5段。
1段目の個数が多い方から4番目のものは、8個、7個、6個、5個の順で5個となります。1段目が5個で確定なので、あとは和が7になる4個の整数の組合せを調べる和分解に帰着します。
周回の旅人算ですが、内容は円周上の点の移動です。このあと、詳説します。
合否を分けた一題
2021年度は、昨年2020年度と比べて格段に難化しました。ただ、取り扱っているテーマは桜蔭算数の過去の出題例から外れるものはほとんどなく、入試を迎えるまでの桜蔭対策の精度がそのまま得点差に表れるセットでした。
1枚目は大問Ⅰ(1)~(3)でどれだけ失点を防いだか、大問Ⅱでの時間のロスを最小限に食い止めたか、2枚目は残り時間を配分して大問Ⅲ・Ⅳをどれだけ得点できたか、がカギです。
このうち、時間の負荷がかかる中で解き進めたであろう大問Ⅲと大問Ⅳのうち、適切な解法を選択できたかが問われる大問Ⅳを今年度の合否を分けた一題として取り上げます。
(1)
円周率が3.1であることに留意して、距離÷速さで時間を求めます。
A 100×3.1÷50=6.2分
B 120×3.1÷50=7.44分
(2)
ここからは角速度を利用します。
A、Bともに煩雑な分数の速さになりますが、それも桜蔭算数では折り込み済み。気に留めずに解き進めましょう。
どうしても数値の煩雑さが気になる場合には、速さは比にして時間を求め、A、Bどちらかの1周分の時間と比較する手法でも構いません。
≪前者の解法≫
それぞれの角速度を求めます。
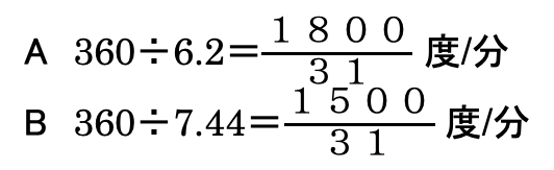
1回目のベルは180度はなれたときなので
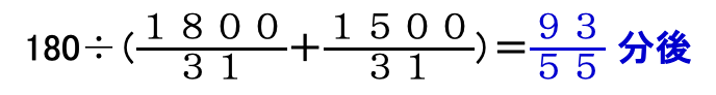
2回目のベルについては、迷いが出た受験生がいるかもしれません。
ベルが鳴るのは「AとBのいる位置を結ぶ直線が点Oを通るとき」
直線の定義は数学で学ぶので、小学生のうちは直線と線分が同じものと認識している可能性があります。ここでの直線を線分ととらえてしまった受験生は、ベルが鳴るのは常に180度はなれた状態となるので、2回目は1回目の3倍となってしまいます。
ベルが鳴るのは、正しくは、同じ位置にいる(0度はなれている)ときか180度はなれているときのどちらかです。
よって、2回目は1回目の2倍になるので、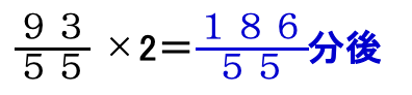
≪後者の解法≫
煩雑な分数の角速度を避けたいのであれば、角速度の比を利用します。
1周の時間の比がAとBで、6.2:7.44=5:6より、角速度の比は6:5
Aの角速度6度/分、Bの角速度5度/分とすると
1回目のベルは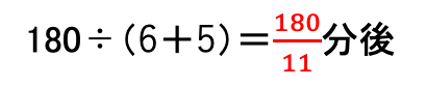
Aが1周するのにかかる時間は、角速度の比で考えると、360÷6=60分
これが6.2分にあたるので、1回目のベルは、6.2÷60×18011=9355分後
2回目のベルは 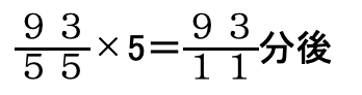
(3)
つるかめ算で解けるのは容易に判断できるでしょう。ただ、数値が煩雑ゆえに、計算が非常に面倒です。
ここでは、比を利用して、処理量をおさえましょう。
5回目のベルは9355×5=9311分後
速さの和の比が 100m/分:140m/分=5:7 より
時間の比は ⑦:⑤
この差の②が1分にあたるので
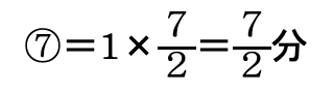
よって、速さを変えたのは、出発してから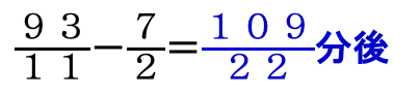
桜蔭中入試対策・関連記事一覧
桜蔭中入試対策・同じ教科(算数)の記事
- 算数の出題傾向分析
- 算数の合格戦略の提案
- 算数の合否を分けた一題(2010年度)
- 時期による算数の学習法の提案(5年生)
- 時期による算数の学習法の提案(6年生)夏休みまで
- 時期による算数の学習法の提案(6年生)秋以降
- 塾ごとの算数の学習法の提案(サピックス生)
- 塾ごとの算数の学習法の提案(四谷大塚生)
- 塾ごとの算数の学習法の提案(日能研生)
- 算数担当講師から桜蔭中学入学を目指す受験生へのアドバイス
- 算数の合否を分けた一題(2012年度)
- 算数の合否を分けた一題(2013年度)
- 算数の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2020年度)
桜蔭中入試対策・同じテーマ(合否を分けた一題)の記事
- 国語の合否を分けた一題(2010年度)
- 算数の合否を分けた一題(2010年度)
- 理科の合否を分けた一題(2010年度)
- 社会の合否を分けた一題(2010年度)
- 国語の合否を分けた一題(2011年度)
- 算数の合否を分けた一題(2012年度)
- 社会の合否を分けた一題(2012年度)
- 理科の合否を分けた一題(2012年度)
- 国語の合否を分けた一題(2013年度)
- 算数の合否を分けた一題(2013年度)
- 社会の合否を分けた一題(2013年度)
- 理科の合否を分けた一題(2013年度)
- 国語の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2015年度)
- 理科の合否を分けた一題(2011年度)
- 理科の合否を分けた一題(2014年度)
- 理科の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2016年度)
- 理科の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2016年度)
- 国語の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2017年度)
- 国語の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2017年度)
- 国語の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2019年度)
- 理科の合否を分けた一題(2019年度)
- 社会の合否を分けた一題(2019年度)
- 国語の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2020年度)
- 理科の合否を分けた一題(2020年度)
- 社会の合否を分けた一題(2020年度)
- 国語の合否を分けた一題(2020年度)
- 社会の合否を分けた一題(2021年度)
- 理科の合否を分けた一題(2021年度)






